江苏省徐州市2021年中考数学试卷
试卷更新日期:2021-07-27 类型:中考真卷
一、单选题
-
1. -3的相反数是( )A、3 B、-3 C、 D、2. 下列图形,是轴对称图形但不是中心对称图形的是( )A、
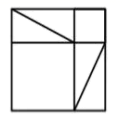 B、
B、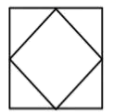 C、
C、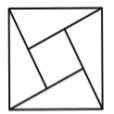 D、
D、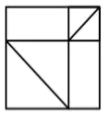 3. 下列计算正确的是( )A、 B、 C、 D、4. 甲、乙两个不透明的袋子中各有三种颜色的糖果若干,这些糖果除颜色外无其他差别.具体情况如下表所示.
3. 下列计算正确的是( )A、 B、 C、 D、4. 甲、乙两个不透明的袋子中各有三种颜色的糖果若干,这些糖果除颜色外无其他差别.具体情况如下表所示.袋子 糖果
红色
黄色
绿色
总计
甲袋
2颗
2颗
1颗
5颗
乙袋
4颗
2颗
4颗
10颗
若小明从甲、乙两个袋子中各随机摸出一颗糖果,则他从甲袋比从乙袋( )
A、摸出红色糖果的概率大 B、摸出红色糖果的概率小 C、摸出黄色糖果的概率大 D、摸出黄色糖果的概率小5. 第七次全国人民普查的部分结果如图所示.
根据该统计图,下列判断错误的是( )
A、徐州0-14岁人口比重高于全国 B、徐州15-59岁人口比重低于江苏 C、徐州60岁以上人口比重高于全国 D、徐州60岁以上人口比重高于江苏6. 下列无理数,与3最接近的是( )A、 B、 C、 D、7. 在平面直角坐标系中,将二次函数 的图象向左平移2个单位长度,再向上平移1个单位长度,所得抛物线对应的函数表达式为( )A、 B、 C、 D、8. 如图,一枚圆形古钱币的中间是一个正方形孔,已知圆的直径与正方形的对角线之比为3:1,则圆的面积约为正方形面积的( ) A、27倍 B、14倍 C、9倍 D、3倍
A、27倍 B、14倍 C、9倍 D、3倍二、填空题
-
9. 我市2020年常住人口约9080000人,该人口数用科学记数法可表示为人.10. 49的平方根是 .11. 因式分解:x2-36= .12. 为使 有意义,则x的取值范围是.13. 若 是方程 的两个根,则 .14. 如图, 是 的直径,点 在 上,若 ,则 °.
 15. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若母线长 为 ,扇形的圆心角 ,则圆锥的底面圆半径 为 .
15. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若母线长 为 ,扇形的圆心角 ,则圆锥的底面圆半径 为 . 16. 如图,在 中,点 分别在边 上,且 , 与四边形 的面积的比为.
16. 如图,在 中,点 分别在边 上,且 , 与四边形 的面积的比为.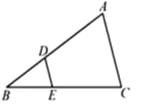 17. 如图,点 分别在函数 的图象上,点 在 轴上.若四边形 为正方形,点 在第一象限,则 的坐标是.
17. 如图,点 分别在函数 的图象上,点 在 轴上.若四边形 为正方形,点 在第一象限,则 的坐标是.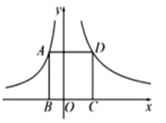 18. 如图,四边形 与 均为矩形,点 分别在线段 上.若 ,矩形 的周长为 ,则图中阴影部分的面积为 .
18. 如图,四边形 与 均为矩形,点 分别在线段 上.若 ,矩形 的周长为 ,则图中阴影部分的面积为 .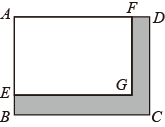
三、解答题
-
19. 计算:(1)、(2)、20.(1)、解方程:(2)、解不等式组:21. 如图, 为 的直径,点 在 上, 与 交于点 , ,连接 .求证:
 (1)、 ;(2)、四边形 是菱形.22. 如图,将一张长方形纸片 沿 折叠,使 两点重合.点 落在点 处.已知 , .
(1)、 ;(2)、四边形 是菱形.22. 如图,将一张长方形纸片 沿 折叠,使 两点重合.点 落在点 处.已知 , .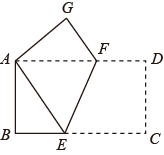 (1)、求证: 是等腰三角形;(2)、求线段 的长.23. 某网店开展促销活动,其商品一律按8折销售,促销期间用400元在该网店购得某商品的数量较打折前多出2件.问:该商品打折前每件多少元?24. 如图,是一个竖直放置的钉板,其中,黑色圆面表示钉板上的钉子, 分别表示相邻两颗钉子之间的空隙,这些空隙大小均相等,从入口 处投放一个直径略小于两颗钉子之间空隙的圆球,圆球下落过程中,总是碰到空隙正下方的钉子,且沿该钉子左右两个相邻空隙继续下落的机会相等,直至圆球落入下面的某个槽内.用画树状图的方法,求圆球落入③号槽内的概率.
(1)、求证: 是等腰三角形;(2)、求线段 的长.23. 某网店开展促销活动,其商品一律按8折销售,促销期间用400元在该网店购得某商品的数量较打折前多出2件.问:该商品打折前每件多少元?24. 如图,是一个竖直放置的钉板,其中,黑色圆面表示钉板上的钉子, 分别表示相邻两颗钉子之间的空隙,这些空隙大小均相等,从入口 处投放一个直径略小于两颗钉子之间空隙的圆球,圆球下落过程中,总是碰到空隙正下方的钉子,且沿该钉子左右两个相邻空隙继续下落的机会相等,直至圆球落入下面的某个槽内.用画树状图的方法,求圆球落入③号槽内的概率.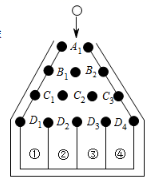 25. 某市近年参加初中学业水平考试的人数(以下简称“中考人数”)的情况如图所示.
25. 某市近年参加初中学业水平考试的人数(以下简称“中考人数”)的情况如图所示.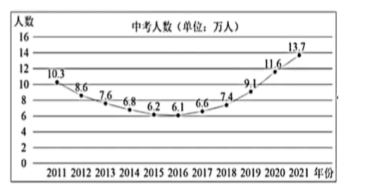
根据图中信息,解决下列问题:
(1)、这11年间,该市中考人数的中位数是万人;(2)、与上年相比,该市中考人数增加最多的年份是年;(3)、下列选项中,与该市2022年中考人数最有可能接近的是( )A、12.8万人 ; B、14.0万人; C、15.3万人(4)、2019年上半年,该市七、八、九三个年级的学生总数约为( )A、23.1万人; B、28.1万人; C、34.4万人(5)、该市2019年上半年七、八、九三个年级的数学教师共有4000人,若保持数学教师与学生的人数之比不变,根据(3)(4)的结论,该市2020年上半年七、八、九三个年级的数学教师较上年同期增加多少人(结果取整数)?26. 如图,点 在函数 的图象上.已知 的横坐标分别为-2、4,直线 与 轴交于点 ,连接 .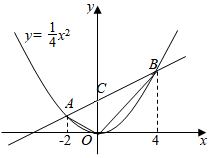 (1)、求直线 的函数表达式;(2)、求 的面积;(3)、若函数 的图象上存在点 ,使得 的面积等于 的面积的一半,则这样的点 共有个.27. 如图,斜坡 的坡角 ,计划在该坡面上安装两排平行的光伏板.前排光伏板的一端位于点 ,过其另一端 安装支架 , 所在的直线垂直于水平线 ,垂足为点 为 与 的交点.已知 ,前排光伏板的坡角 .
(1)、求直线 的函数表达式;(2)、求 的面积;(3)、若函数 的图象上存在点 ,使得 的面积等于 的面积的一半,则这样的点 共有个.27. 如图,斜坡 的坡角 ,计划在该坡面上安装两排平行的光伏板.前排光伏板的一端位于点 ,过其另一端 安装支架 , 所在的直线垂直于水平线 ,垂足为点 为 与 的交点.已知 ,前排光伏板的坡角 .参考数据:
三角函数锐角
13°
28°
32°
0.22
0.47
0.53
0.97
0.88
0.85
0.23
0.53
0.62
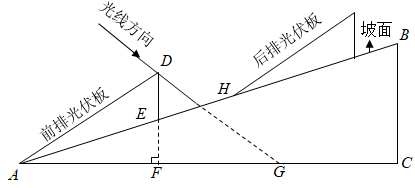 (1)、求 的长(结果取整数);(2)、冬至日正午,经过点 的太阳光线与 所成的角 .后排光伏板的前端 在 上.此时,若要后排光伏板的采光不受前排光伏板的影响,则 的最小值为多少(结果取整数)?28. 如图1,正方形 的边长为4,点 在边 上( 不与 重合),连接 .将线段 绕点 顺时针旋转90°得到 ,将线段 绕点 逆时针旋转90°得到 .连接 .
(1)、求 的长(结果取整数);(2)、冬至日正午,经过点 的太阳光线与 所成的角 .后排光伏板的前端 在 上.此时,若要后排光伏板的采光不受前排光伏板的影响,则 的最小值为多少(结果取整数)?28. 如图1,正方形 的边长为4,点 在边 上( 不与 重合),连接 .将线段 绕点 顺时针旋转90°得到 ,将线段 绕点 逆时针旋转90°得到 .连接 .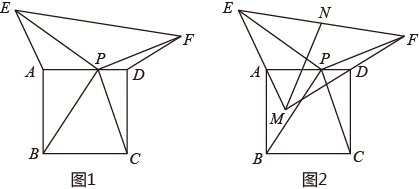 (1)、求证:
(1)、求证:① 的面积 ;
② ;
(2)、如图2, 的延长线交于点 ,取 的中点 ,连接 ,求 的取值范围.