江苏省泰州市2021年中考数学试卷
试卷更新日期:2021-07-27 类型:中考真卷
一、单选题
-
1. (﹣3)0等于( )A、0 B、1 C、3 D、﹣32. 如图所示几何体的左视图是( )
 A、
A、 B、
B、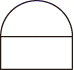 C、
C、 D、
D、 3. 下列各组二次根式中,化简后是同类二次根式的是( )A、 与 B、 与 C、 与 D、 与4. “14人中至少有2人在同一个月过生日”这一事件发生的概率为P,则( )A、P=0 B、0<P<1 C、P=1 D、P>15. 如图,P为AB上任意一点,分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF,设 ,则 为( )
3. 下列各组二次根式中,化简后是同类二次根式的是( )A、 与 B、 与 C、 与 D、 与4. “14人中至少有2人在同一个月过生日”这一事件发生的概率为P,则( )A、P=0 B、0<P<1 C、P=1 D、P>15. 如图,P为AB上任意一点,分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF,设 ,则 为( )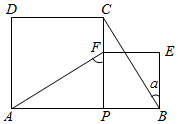 A、2α B、90°﹣α C、45°+α D、90°﹣ α6. 互不重合的A、B、C三点在同一直线上,已知AC=2a+1,BC=a+4,AB=3a,这三点的位置关系是( )A、点A在B、C两点之间 B、点B在A、C两点之间 C、点C在A、B两点之间 D、无法确定
A、2α B、90°﹣α C、45°+α D、90°﹣ α6. 互不重合的A、B、C三点在同一直线上,已知AC=2a+1,BC=a+4,AB=3a,这三点的位置关系是( )A、点A在B、C两点之间 B、点B在A、C两点之间 C、点C在A、B两点之间 D、无法确定二、填空题
-
7. 计算:﹣(﹣2)=.8. 函数:y=中,自变量x的取值范围是9. 2021年5月,中国首个火星车“祝融号”成功降落在火星上直径为3200km的乌托邦平原.把数据3200用科学记数法表示为 .10. 在函数 中,当x>1时,y随x的增大而 .(填“增大”或“减小”)11. 某班按课外阅读时间将学生分为3组,第1、2组的频率分别为0.2、0.5,则第3组的频率是 .12. 关于x的方程x2﹣x﹣1=0的两根分别为x1、x2则x1+x2﹣x1•x2的值为 .13. 已知扇形的半径为8 cm,圆心角为45°,则此扇形的弧长是cm.
14. 如图,木棒AB、CD与EF分别在G、H处用可旋转的螺丝铆住,∠EGB=100°,∠EHD=80°,将木棒AB绕点G逆时针旋转到与木棒CD平行的位置,则至少要旋转 °.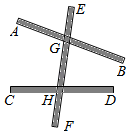 15. 如图,平面直角坐标系xOy中,点A的坐标为(8,5),⊙A与x轴相切,点P在y轴正半轴上,PB与⊙A相切于点B.若∠APB=30°,则点P的坐标为 .
15. 如图,平面直角坐标系xOy中,点A的坐标为(8,5),⊙A与x轴相切,点P在y轴正半轴上,PB与⊙A相切于点B.若∠APB=30°,则点P的坐标为 .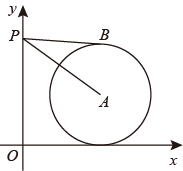 16. 如图,四边形ABCD中,AB=CD=4,且AB与CD不平行,P、M、N分别是AD、BD、AC的中点,设△PMN的面积为S,则S的范围是 .
16. 如图,四边形ABCD中,AB=CD=4,且AB与CD不平行,P、M、N分别是AD、BD、AC的中点,设△PMN的面积为S,则S的范围是 .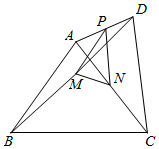
三、解答题
-
17.(1)、分解因式:x3﹣9x;(2)、解方程: +1= .18. 近5年,我省家电业的发展发生了新变化.以甲、乙、丙3种家电为例,将这3种家电2016~2020年的产量(单位:万台)绘制成如图所示的折线统计图,图中只标注了甲种家电产量的数据.

观察统计图回答下列问题:
(1)、这5年甲种家电产量的中位数为 万台;(2)、若将这5年家电产量按年份绘制成5个扇形统计图,每个统计图只反映该年这3种家电产量占比,其中有一个扇形统计图的某种家电产量占比对应的圆心角大于180°,这个扇形统计图对应的年份是 年;(3)、小明认为:某种家电产量的方差越小,说明该家电发展趋势越好.你同意他的观点吗?请结合图中乙、丙两种家电产量变化情况说明理由.19. 江苏省第20届运动会将在泰州举办,“泰宝”和“凤娃”是运动会吉祥物.在一次宣传活动中,组织者将分别印有这两种吉祥物图案的卡片各2张放在一个不透明的盒子中并搅匀,卡片除图案外其余均相同.小张从中随机抽取2张换取相应的吉祥物,抽取方式有两种:第一种是先抽取1张不放回,再抽取1张;第二种是一次性抽取2张.(1)、两种抽取方式抽到不同图案卡片的概率 (填“相同”或“不同”);(2)、若小张用第一种方式抽取卡片,求抽到不同图案卡片的概率.20. 甲、乙两工程队共同修建150km的公路,原计划30个月完工.实际施工时,甲队通过技术创新,施工效率提高了50%,乙队施工效率不变,结果提前5个月完工.甲、乙两工程队原计划平均每月分别修建多长?21. 如图,游客从旅游景区山脚下的地面A处出发,沿坡角α=30°的斜坡AB步行50m至山坡B处,乘直立电梯上升30m至C处,再乘缆车沿长为180m的索道CD至山顶D处,此时观测C处的俯角为19°30′,索道CD看作在一条直线上.求山顶D的高度.(精确到1m,sin19°30′≈0.33,cos19°30′≈0.94,tan19°30′≈0.35)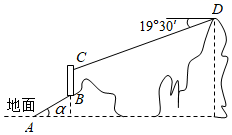 22. 如图,点A(﹣2,y1)、B(﹣6,y2)在反比例函数y= (k<0)的图象上,AC⊥x轴,BD⊥y轴,垂足分别为C、D,AC与BD相交于点E.
22. 如图,点A(﹣2,y1)、B(﹣6,y2)在反比例函数y= (k<0)的图象上,AC⊥x轴,BD⊥y轴,垂足分别为C、D,AC与BD相交于点E.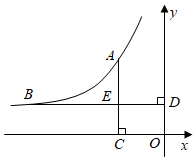 (1)、根据图象直接写出y1、y2的大小关系,并通过计算加以验证;(2)、结合以上信息,从①四边形OCED的面积为2,②BE=2AE这两个条件中任选一个作为补充条件,求k的值.你选择的条件是 ▲ (只填序号).23. 如图
(1)、根据图象直接写出y1、y2的大小关系,并通过计算加以验证;(2)、结合以上信息,从①四边形OCED的面积为2,②BE=2AE这两个条件中任选一个作为补充条件,求k的值.你选择的条件是 ▲ (只填序号).23. 如图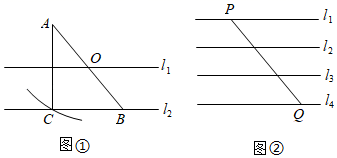 (1)、如图①,O为AB的中点,直线l1、l2分别经过点O、B,且l1∥l2 , 以点O为圆心,OA长为半径画弧交直线l2于点C,连接AC.求证:直线l1垂直平分AC;(2)、如图②,平面内直线l1∥l2∥l3∥l4 , 且相邻两直线间距离相等,点P、Q分别在直线l1、l4上,连接PQ.用圆规和无刻度的直尺在直线l4上求作一点D,使线段PD最短.(两种工具分别只限使用一次,并保留作图痕迹)24. 农技人员对培育的某一品种桃树进行研究,发现桃子成熟后一棵树上每个桃子质量大致相同.以每棵树上桃子的数量x(个)为横坐标、桃子的平均质量y(克/个)为纵坐标,在平面直角坐标系中描出对应的点,发现这些点大致分布在直线AB附近(如图所示).
(1)、如图①,O为AB的中点,直线l1、l2分别经过点O、B,且l1∥l2 , 以点O为圆心,OA长为半径画弧交直线l2于点C,连接AC.求证:直线l1垂直平分AC;(2)、如图②,平面内直线l1∥l2∥l3∥l4 , 且相邻两直线间距离相等,点P、Q分别在直线l1、l4上,连接PQ.用圆规和无刻度的直尺在直线l4上求作一点D,使线段PD最短.(两种工具分别只限使用一次,并保留作图痕迹)24. 农技人员对培育的某一品种桃树进行研究,发现桃子成熟后一棵树上每个桃子质量大致相同.以每棵树上桃子的数量x(个)为横坐标、桃子的平均质量y(克/个)为纵坐标,在平面直角坐标系中描出对应的点,发现这些点大致分布在直线AB附近(如图所示).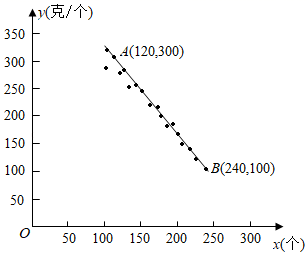 (1)、求直线AB的函数关系式;(2)、市场调研发现:这个品种每个桃子的平均价格w(元)与平均质量y(克/个)满足函数表达式w= y+2.在(1)的情形下,求一棵树上桃子数量为多少时,该树上的桃子销售额最大?25. 二次函数y=﹣x2+(a﹣1)x+a(a为常数)图象的顶点在y轴右侧.(1)、写出该二次函数图象的顶点横坐标(用含a的代数式表示);(2)、该二次函数表达式可变形为y=﹣(x﹣p)(x﹣a)的形式,求p的值;(3)、若点A(m,n)在该二次函数图象上,且n>0,过点(m+3,0)作y轴的平行线,与二次函数图象的交点在x轴下方,求a的范围.26. 如图,在⊙O中,AB为直径,P为AB上一点,PA=1,PB=m(m为常数,且m>0).过点P的弦CD⊥AB,Q为 上一动点(与点B不重合),AH⊥QD,垂足为H.连接AD、BQ.
(1)、求直线AB的函数关系式;(2)、市场调研发现:这个品种每个桃子的平均价格w(元)与平均质量y(克/个)满足函数表达式w= y+2.在(1)的情形下,求一棵树上桃子数量为多少时,该树上的桃子销售额最大?25. 二次函数y=﹣x2+(a﹣1)x+a(a为常数)图象的顶点在y轴右侧.(1)、写出该二次函数图象的顶点横坐标(用含a的代数式表示);(2)、该二次函数表达式可变形为y=﹣(x﹣p)(x﹣a)的形式,求p的值;(3)、若点A(m,n)在该二次函数图象上,且n>0,过点(m+3,0)作y轴的平行线,与二次函数图象的交点在x轴下方,求a的范围.26. 如图,在⊙O中,AB为直径,P为AB上一点,PA=1,PB=m(m为常数,且m>0).过点P的弦CD⊥AB,Q为 上一动点(与点B不重合),AH⊥QD,垂足为H.连接AD、BQ.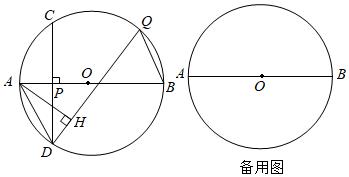 (1)、若m=3.
(1)、若m=3.①求证:∠OAD=60°;
②求 的值;
(2)、用含m的代数式表示 ,请直接写出结果;(3)、存在一个大小确定的⊙O,对于点Q的任意位置,都有BQ2﹣2DH2+PB2的值是一个定值,求此时∠Q的度数.