天津市滨海新区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-07-26 类型:期末考试
一、单选题
-
1. 若 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、2. 下列各式中,是最简二次根式的是( )A、 B、 C、 D、3. 下列四组线段中,不能构成直角三角形的是( )A、3,4,5 B、2,3,4 C、 D、13,12,54. 下列曲线中不能表示 是 的函数的是( )A、
 B、
B、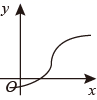 C、
C、 D、
D、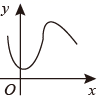 5. 在平行四边形ABCD中,若 ,则 的度数是( )A、 B、 C、 D、6. 在平面直角坐标系中,下列各点在直线 上的是( )A、 B、 C、 D、7. 用配方法解方程 时,原方程变形正确的是( )A、 B、 C、 D、8. 如图Rt 中, ,分别以边AB,CA,BC向外做正方形,正方形ABIH的面积为25,正方形ACFG的面积为144,则正方形BDEC的面积是( )
5. 在平行四边形ABCD中,若 ,则 的度数是( )A、 B、 C、 D、6. 在平面直角坐标系中,下列各点在直线 上的是( )A、 B、 C、 D、7. 用配方法解方程 时,原方程变形正确的是( )A、 B、 C、 D、8. 如图Rt 中, ,分别以边AB,CA,BC向外做正方形,正方形ABIH的面积为25,正方形ACFG的面积为144,则正方形BDEC的面积是( ) A、130 B、119 C、169 D、1209. 一元二次方程 的根的情况是( )A、有两个相等的实数根 B、没有实数根 C、有两个不相等的实数根 D、只有一个实数根10. 如图,在正方形ABCD的外侧,作等边三角形ADE,则∠AEB为( )
A、130 B、119 C、169 D、1209. 一元二次方程 的根的情况是( )A、有两个相等的实数根 B、没有实数根 C、有两个不相等的实数根 D、只有一个实数根10. 如图,在正方形ABCD的外侧,作等边三角形ADE,则∠AEB为( )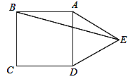 A、10° B、15° C、20° D、125°11. 已知张强家、体育场、文具店在同一直线上.如图图像反映的过程是:张强从家跑步去体育场,在体育场锻炼了一阵后又走到文具店去买钢笔,然后散步走回家,图中 表示时间, 表示张强离家的距离,则下列结论错误的是( )
A、10° B、15° C、20° D、125°11. 已知张强家、体育场、文具店在同一直线上.如图图像反映的过程是:张强从家跑步去体育场,在体育场锻炼了一阵后又走到文具店去买钢笔,然后散步走回家,图中 表示时间, 表示张强离家的距离,则下列结论错误的是( )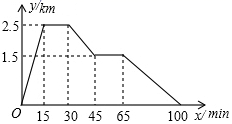 A、体育场离张强家2.5 km B、体育场离文具店1 km C、张强在文具店停留20min D、张强从文具店回到家的平均速度为25m/min12. 如图,矩形纸片ABCD中,AB=4,BC=8,点E和点F分别是边BC,AD上的点,将纸片沿EF折叠,使点C与点A重合,下列结论错误的是( )
A、体育场离张强家2.5 km B、体育场离文具店1 km C、张强在文具店停留20min D、张强从文具店回到家的平均速度为25m/min12. 如图,矩形纸片ABCD中,AB=4,BC=8,点E和点F分别是边BC,AD上的点,将纸片沿EF折叠,使点C与点A重合,下列结论错误的是( ) A、AF=AE B、 C、 D、AE=EF
A、AF=AE B、 C、 D、AE=EF二、填空题
-
13. 已知关于 的方程 的一个根为 ,则k= .14. 一次函数 与y轴交点坐标为 .15. 直角三角形两直角边长分别为3和4,则它斜边上的高为 .16. 当 时,代数式 的值是 .17. 如图点E是正方形ABCD的对角线BD上一点,EF⊥BC,EG⊥CD,垂足分别是F,G,GF=4,则AE= .

三、解答题
-
18. 如图,在每个小正方形的边长为1的网格中,点A,B,O,P均在格点上.
 (1)、OB的长等于;(2)、点M在射线OA上,点N在射线OB上,当ΔPMN的周长最小时,请在如图所示的网格中,用无刻度的直尺,画出ΔPMN,并简要说明点M,N的位置是如何找到的(不要求证明).19. 计算下列各题:(1)、 ;(2)、 .20. 解下列方程:
(1)、OB的长等于;(2)、点M在射线OA上,点N在射线OB上,当ΔPMN的周长最小时,请在如图所示的网格中,用无刻度的直尺,画出ΔPMN,并简要说明点M,N的位置是如何找到的(不要求证明).19. 计算下列各题:(1)、 ;(2)、 .20. 解下列方程:(Ⅰ) ;
(Ⅱ) .
21. 如图,在平行四边形ABCD中,对角线AC,BD相交于点O,且点M,N分别是OB,OD的中点,连接AN,CM.求证:AN=CM. 22. 如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
22. 如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF. (1)、求证:CE=CF.(2)、连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.23. 某超市超市准备购进A、B两种品牌的书包共100个,已知两种书包的进价如下表所示,设购进A种书包x个,且所购进的两种书包能全部卖出,获得的总利润为y元.(1)、将表格的信息填写完整;
(1)、求证:CE=CF.(2)、连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.23. 某超市超市准备购进A、B两种品牌的书包共100个,已知两种书包的进价如下表所示,设购进A种书包x个,且所购进的两种书包能全部卖出,获得的总利润为y元.(1)、将表格的信息填写完整;品牌
购买个数(个)
进价(元/个)
售价(元/个)
获利(元)
A
x
50
60
▲
B
▲
40
55
▲
(2)、求y关于x的函数表达式;(3)、如果购进两种书包的总费用不超过4500元且购进B种书包的数量不大于A种书包的3倍,那么超市如何进货才能获利最大?并求出最大利润.24. 如图,将长方形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将长方形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E. (1)、当m=3时,点B的坐标为 , 点E的坐标为;(2)、随着m的变化,试探索:点E能否恰好落在x轴上?若能,请求出m的值;若不能,请说明理由.25. 如图1,矩形 摆放在平面直角坐标系中,点 在 轴上,点 在 轴上, , ,过点 的直线交矩形 的边 于点 ,且点 不与点 、 重合,过点 作 , 交 轴于点 ,交 轴于点 .
(1)、当m=3时,点B的坐标为 , 点E的坐标为;(2)、随着m的变化,试探索:点E能否恰好落在x轴上?若能,请求出m的值;若不能,请说明理由.25. 如图1,矩形 摆放在平面直角坐标系中,点 在 轴上,点 在 轴上, , ,过点 的直线交矩形 的边 于点 ,且点 不与点 、 重合,过点 作 , 交 轴于点 ,交 轴于点 . (1)、若 为等腰直角三角形.
(1)、若 为等腰直角三角形.①直接写出此时 点的坐标: ▲ ;直线 的解析式为 ▲ ;
②在 轴上另有一点 的坐标为 ,请在直线 和 轴上分别找一点 、 ,使 的周长最小,并求出此时点 的坐标和 周长的最小值.
(2)、如图2,过点 作 交 轴于点 ,若以 、 、 、 为顶点的四边形是平行四边形,求直线 的解析式.