上海市闵行区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-07-26 类型：期末考试

进入出卷网下载

一、单选题

1. 下列函数中，是一次函数的是（）

A、 $y = \frac{1}{x} + 1$ B、 $x + 3 y = 1$ C、 $y = x^{2} - 1$ D、 $y = 2$

查看试题解析
2. 如果关于 $x$ 的方程 $\sqrt{2 x + m} = x$ 有实数根 $x = 1$ ，那么m的值是（）

A、 $- 1$ B、 $\frac{1}{3}$ C、 $0$ D、 $2$

查看试题解析
3. 用换元法解方程 $\frac{x + 1}{x^{2}}$ + $\frac{x^{2}}{x + 1}$ =2时，若设 $\frac{x + 1}{x^{2}}$ =y ，则原方程可化为关于y的方程是（）

A、y²﹣2y+1=0 B、y²+2y+1=0 C、y²+y+2=0 D、y²+y﹣2=0

查看试题解析
4. 从一副未曾启封的扑克牌中取出1张红桃，2张黑桃的牌共3张，洗匀后，从这3张牌中任取1张牌恰好是黑桃的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $1$

查看试题解析
5. 已知四边形 $A B C D$ 是平行四边形，下列结论中错误的是（）

A、当 $A C = B D$ 时，四边形 $A B C D$ 是正方形 B、当 $A C ⊥ B D$ 时，四边形 $A B C D$ 是菱形 C、当 $A B = B C$ 时，四边形 $A B C D$ 是菱形 D、当 $∠ A B C = 90 °$ 时，四边形 $A B C D$ 是矩形

查看试题解析
6. 我们把梯形下底与上底的差叫做梯形的底差，梯形的高与中位线的比值叫做梯形的纵横比．如果一个腰长为 $5$ 的等腰梯形，底差等于 $6$ ，面积为 $24$ ，那么这个等腰梯形的纵横比等于（）

A、 $\frac{5}{4}$ B、 $\frac{5}{6}$ C、 $\frac{2}{3}$ D、 $\frac{3}{5}$

查看试题解析

二、填空题

7. 一次函数 $y = - x + 1$ 的图像在 $y$ 轴上的截距为．

查看试题解析
8. 如果将直线 $y = \frac{1}{2} x$ 沿 $y$ 轴向下平移2个单位，那么平移后所得直线的表达式是．

查看试题解析
9. 一次函数y＝3x+m﹣1的图象不经过第二象限，则m的取值范围是．

查看试题解析
10. 利用计算器解方程 $2 x^{3} + \frac{1}{54} = 0$ ，所得的近似根是．（保留三个有效数字）

查看试题解析
11. 方程 $\sqrt{x - 1}$ =2的解是

查看试题解析
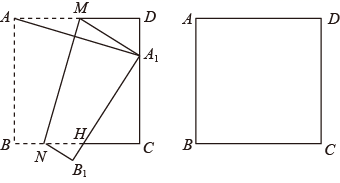
12. 一枚材质均匀的骰子，六个面的点数分别是1，2，3，4，5，6，投这个骰子，掷的的点数大于4的概率是.

查看试题解析
13. 一个多边形的内角和为1440°，则它的边数为

查看试题解析
14. 如果 $| \vec{a} | = 8$ ，方向向西， $| \vec{b} | = 5$ ，方向向东，那么 $| \vec{a} + \vec{b} | =$ ．

查看试题解析
15. 已知 $O$ 是平行四边形 $A B C D$ 的对角线 $A C$ 与 $B D$ 的交点. $A C = 24$ ， $B D = 38$ ， $A D = 28$ ，那么 $Δ O B C$ 的周长等于．

查看试题解析
16. 如图，等腰梯形 $A B C D$ 中， $A D / / B C$ ， $A B = C D$ ，对角线 $A C ⊥ B D$ ，如果高 $D E = 8 c m$ ，那么等腰梯形 $A B C D$ 的中位线的长为cm．

查看试题解析
17. 如图，在 $Δ A B C$ 中， $A B = A C$ ，直线 $D E$ 垂直平分 $A B$ ，把线段 $A E$ 绕点 $E$ 顺时针旋转 $90 °$ ，使点 $A$ 落在直线 $D E$ 上的点 $F$ 处，联结 $C F$ 、 $B F$ ，线段 $A C$ 、 $B F$ 交于点 $G$ ，如果 $C F // A B$ ，那么 $∠ A G B =$ 度．

查看试题解析
18. 如图，点 $M$ 的坐标为 $(3 ， 2)$ ，点 $P$ 从原点 $O$ 出发，以每秒 $1$ 个单位的速度沿 $y$ 轴向上移动，同时过点 $P$ 的直线关于直线 $l$ 也随之上下平移，且直线 $l$ 与直线 $y = - x$ 平行，如果点 $M$ 关于直线 $l$ 的对称点落在坐标轴上，如果点 $P$ 的移动时间为 $t$ 秒，那么 $t$ 的值为．

查看试题解析

三、解答题

19. 解关于 $x$ 的方程： $a^{2} x^{2} - 1 = - x^{2}$ ．

查看试题解析
20. 解方程组： ${\begin{array}{l} x - y = 2 ， \\ x^{2} - 2 x y - 3 y^{2} = 0. \end{array}$

查看试题解析
21. 闵行区政府为提高道路的绿化率，在道路两边进行植工程，计划第一期先栽种 $1500$ 棵梧桐树. 为了加快进度，绿化队在实际栽种时增加了植树人员，每天栽种的梧桐树比原计划多 $200$ 棵，结果提前 $2$ 天完成任务．求实际每天栽种多少棵梧桐树？

查看试题解析
22. 如图，已知点 $E$ 在矩形 $A B C D$ 的边 $D C$ 上，且 $A B = A E = 2 A D$ ．求 $∠ E B C$ 的度数．

查看试题解析
23. 如图，已知在梯形 $A B C D$ 中， $A D // B C$ ， $∠ B = 90 °$ ，点 $E$ 是对角线 $A C$ 的中点，联结 $D E$ 并延长，交边 $B C$ 于点 $F$ ，联结 $A F$ ．

(1)、求证：四边形 $A F C D$ 是平行四边形；

(2)、联结 $B E$ ，如果 $A F$ 垂直平分 $B E$ ，求证：四边形 $A F C D$ 是菱形．

查看试题解析
24. 已知一次函数 $y = k x + 2$ 的图像与 $x$ 轴交于点 $A$ ，与 $y$ 轴交于点 $B$ ，且 $Δ A O B$ 的面积为 $4$ ，函数值 $y$ 随自变量 $x$ 的值增大而减小．

(1)、求直线 $y = k x + 2$ 的表达式，并画出函数图象；

(2)、以线段 $A B$ 为底边在第一象限作等腰直角三角形 $A B C$ （ $C B = C A$ ， $∠ C = 90 °$ ），求点 $C$ 的坐标．

查看试题解析
25. 如图，已知正方形 $A B C D$ 的边长为 $4$ ，点 $A_{1}$ 为边 $C D$ 上的一个动点（不与点 $C$ 、 $D$ 重合），将正方形纸片翻折，使得点 $A$ 落在点 $A_{1}$ 处，点 $B$ 落在点 $B_{1}$ 处， $A_{1} B_{1}$ 交边 $B C$ 于点 $H$ ，折痕为 $M N$ ，联结 $A A_{1}$ 交边 $M N$ 于点 $O$ ．

(1)、求证： $A A_{1} = M N$ .

(2)、当 $A_{1}$ 在边 $C D$ 的运动时，设 $A_{1} D = x$ ，梯形 $A B N M$ 的面积为 $y$ ，求 $y$ 与 $x$ 之间的函数解析式，并写出定义域．

查看试题解析