山东省泰安市泰山区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-07-26 类型:期末考试
一、单选题
-
1. 下面四组线段中,成比例的是( )A、a=2,b=3,c=4,d=5 B、a=1,b=2,c=2,d=4 C、a=4,b=6,c=8,d=10 D、a= ,b= ,c=3,d=2. 如图,在 中, ,且 ,则 的值为( )
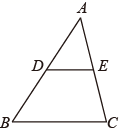 A、 B、 C、 D、3. 等式 成立的条件是( )A、 B、 且 C、 D、4. 用因式分解法解一元二次方程 时,原方程可化为( )A、 B、 C、 D、5. 下列二次根式的运算正确的是( )A、 B、 C、 D、6. 若 是关于 的一元二次方程 的一个根,则 的值为( )A、 B、 C、 D、7. 如图所示,在△ABC 中,AB=6,AC=4,P 是AC 的中点,过 P 点的直线交AB 于点Q,若以 A、P、Q 为顶点的三角形和以A、B、C为顶点的三角形相似,则AQ 的长为 ( )
A、 B、 C、 D、3. 等式 成立的条件是( )A、 B、 且 C、 D、4. 用因式分解法解一元二次方程 时,原方程可化为( )A、 B、 C、 D、5. 下列二次根式的运算正确的是( )A、 B、 C、 D、6. 若 是关于 的一元二次方程 的一个根,则 的值为( )A、 B、 C、 D、7. 如图所示,在△ABC 中,AB=6,AC=4,P 是AC 的中点,过 P 点的直线交AB 于点Q,若以 A、P、Q 为顶点的三角形和以A、B、C为顶点的三角形相似,则AQ 的长为 ( )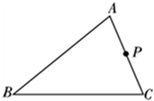 A、3 B、3或 C、3或 D、8. 如图,将矩形 折叠,使点C和点A重合,折痕为 , 与 交于点O若 , ,则 的长为( )
A、3 B、3或 C、3或 D、8. 如图,将矩形 折叠,使点C和点A重合,折痕为 , 与 交于点O若 , ,则 的长为( )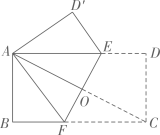 A、 B、 C、 D、9. 如图,在 中, ,高 ,正方形 一边在 上,点 分别在 上, 交 于点 ,则 的长为( )
A、 B、 C、 D、9. 如图,在 中, ,高 ,正方形 一边在 上,点 分别在 上, 交 于点 ,则 的长为( )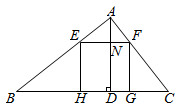 A、 B、 C、 D、10. 如图,在 中, , 是 的中点,过点 作 的平行线,交 于点E,作 的垂线交 于点 ,若 ,且 的面积为1,则 的长为( )
A、 B、 C、 D、10. 如图,在 中, , 是 的中点,过点 作 的平行线,交 于点E,作 的垂线交 于点 ,若 ,且 的面积为1,则 的长为( )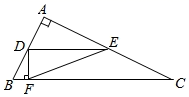 A、 B、5 C、 D、1011. 如图,矩形 中, 为 中点,过点 的直线分别与 、 交于点 、 ,连结 交 于点 ,连结 、 .若 , ,则下列结论:① , ;② ;③四边形 是菱形;④ .其中正确结论的个数是( )
A、 B、5 C、 D、1011. 如图,矩形 中, 为 中点,过点 的直线分别与 、 交于点 、 ,连结 交 于点 ,连结 、 .若 , ,则下列结论:① , ;② ;③四边形 是菱形;④ .其中正确结论的个数是( )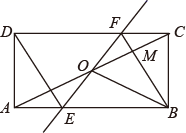 A、 个 B、 个 C、 个 D、 个12. 已知关于x的一元二次方程(a+1)x2+2bx+(a+1)=0有两个相等的实数根,下列判断正确的是( )A、1一定不是关于x的方程x2+bx+a=0的根 B、0一定不是关于x的方程x2+bx+a=0的根 C、1和﹣1都是关于x的方程x2+bx+a=0的根 D、1和﹣1不都是关于x的方程x2+bx+a=0的根
A、 个 B、 个 C、 个 D、 个12. 已知关于x的一元二次方程(a+1)x2+2bx+(a+1)=0有两个相等的实数根,下列判断正确的是( )A、1一定不是关于x的方程x2+bx+a=0的根 B、0一定不是关于x的方程x2+bx+a=0的根 C、1和﹣1都是关于x的方程x2+bx+a=0的根 D、1和﹣1不都是关于x的方程x2+bx+a=0的根二、填空题
-
13. 最简二次根式 和 是同类二次根式,则x的值为14. 若 (a≠2c),则 =15. 关于x的一元二次方程x2+4x+k=0有两个实数根,则k的取值范围是16. 学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4m,AB=1.6m,CO=1m,则栏杆C端应下降的垂直距离CD为.
 17. 如图,周长为40的菱形ABCD中,对角线AC,BD交于点O,H为AD边中点,则OH的长等于
17. 如图,周长为40的菱形ABCD中,对角线AC,BD交于点O,H为AD边中点,则OH的长等于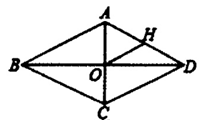 18. 已知 , 为实数,且 ,则 的值是 .19. 下列命题:①所有的等腰三角形都相似;②所有的等边三角形都相似;③所有的等腰直角三角形都相似;④所有的直角三角形都相似;其中真命题是(把所有真命题的序号都填上).20. 如图,在平面直角坐标系中,点A、B的坐标分别为 、 ,点 在第一象限内,连接 、 .已知 ,则 .
18. 已知 , 为实数,且 ,则 的值是 .19. 下列命题:①所有的等腰三角形都相似;②所有的等边三角形都相似;③所有的等腰直角三角形都相似;④所有的直角三角形都相似;其中真命题是(把所有真命题的序号都填上).20. 如图,在平面直角坐标系中,点A、B的坐标分别为 、 ,点 在第一象限内,连接 、 .已知 ,则 .
三、解答题
-
21. 计算(1)、(2)、22. 解下列方程.(1)、 (用配方法);(2)、 .23. 如图,在△ABC中,AB=AC,点D、E分别是线段BC、AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF。
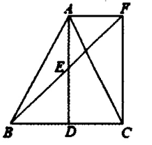
求证:四边形ADCF是矩形。
24. 某口罩生产厂生产的口罩 月份平均日产量为 个, 月底因突然爆发新冠肺炎疫情,市场对口罩需求量大增,为满足市场需求.工厂决定从 月份起扩大产能,则第一季度三个月的平均日产量之和为 个.(1)、求口罩日产量的月平均增长率;(2)、按照这个增长率,预计 月份平均日产量为多少?25. 如图,在 中,点 、 分别在边 , 上, ,线段 分别交线段 , 于点 , ,且 .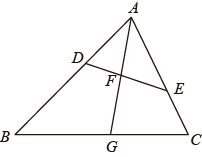 (1)、求证: ;(2)、若 ,求 的值.
(1)、求证: ;(2)、若 ,求 的值.