山东省临沂市罗庄区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-07-26 类型:期末考试
一、单选题
-
1. 下列式子中,y不是x的函数的是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 下列坐标平面内的点,在直线 的是( )A、 B、 C、 D、4. 三边长分别为 , , ,且 ,则 是( )A、直角三角形 B、等边三角形 C、等腰三角形 D、等腰直角三角形5. 某中学规定学生的学期体育成绩满分为100分,其中早锻炼及体育课外活动占20%,期中考试成绩占30%,期末考试成绩占50%.小桐的三项成绩(百分制)依次为95,90,85.则小桐这学期的体育成绩是( )A、88.5 B、86.5 C、90 D、90.56. 下列说法错误的是( )A、对角线互相垂直的平行四边形是矩形 B、矩形的对角线相等 C、对角线相等的菱形是正方形 D、两组对边分别相等的四边形是平行四边形7. 如图, , ,以点A为圆心,AC长为半径画弧,交y轴正半轴于点B,则点B的坐标为( )
 A、 B、 C、 D、8. 一次函数 的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图,已知E是正方形ABCD对角线AC上一点,且AB=AE,则∠DBE度数是( )
A、 B、 C、 D、8. 一次函数 的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图,已知E是正方形ABCD对角线AC上一点,且AB=AE,则∠DBE度数是( ) A、15° B、32.5° C、22.5° D、30°10. 如图,在矩形 中,将 沿 折叠得到 ,延长 交 边于点 ,若 , ,则 的长为( )
A、15° B、32.5° C、22.5° D、30°10. 如图,在矩形 中,将 沿 折叠得到 ,延长 交 边于点 ,若 , ,则 的长为( ) A、4 B、 C、3 D、11. 甲无人机从地面起飞,乙无人机从距离地面20m高的楼顶起飞,两架无人机同时匀速上升10s.甲、乙两架无人机所在的位置距离地面的高度y(单位:m)与无人机上升的时间x(单位:s)之间的关系如图所示.下列说法正确的是( )
A、4 B、 C、3 D、11. 甲无人机从地面起飞,乙无人机从距离地面20m高的楼顶起飞,两架无人机同时匀速上升10s.甲、乙两架无人机所在的位置距离地面的高度y(单位:m)与无人机上升的时间x(单位:s)之间的关系如图所示.下列说法正确的是( )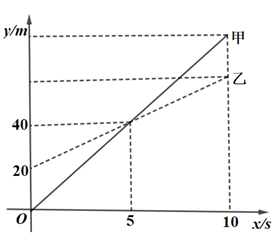 A、5s时,两架无人机都上升了40m B、10s时,两架无人机的高度差为20m C、乙无人机上升的速度为8m/s D、10s时,甲无人机距离地面的高度是60m12. 如图,将长为 ,宽为 的四个矩形如图所示摆放在坐标系中,若正比例函数 的图像恰好将所组成的图形分为面积相等的两部分,则 的值等于( )
A、5s时,两架无人机都上升了40m B、10s时,两架无人机的高度差为20m C、乙无人机上升的速度为8m/s D、10s时,甲无人机距离地面的高度是60m12. 如图,将长为 ,宽为 的四个矩形如图所示摆放在坐标系中,若正比例函数 的图像恰好将所组成的图形分为面积相等的两部分,则 的值等于( )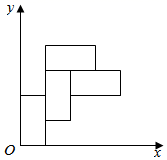 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 数据2,3,5,5,4的众数是 .14. 若函数 是正比例函数,则 .15. 如图,在 中, , 为 的中点,点 在 上,且 , ,则 的大小为 .
 16. 如图 的顶点均在 的正方形网格格点上,若 的坐标为 , 的坐标为 ,作角平分线 ,则 的坐标为(写出一个即可).
16. 如图 的顶点均在 的正方形网格格点上,若 的坐标为 , 的坐标为 ,作角平分线 ,则 的坐标为(写出一个即可). 17. 已知 ,求 .18. 如图,点 是矩形 边 上的一点,点 , , 分别是 , , 的中点, ,则 的长为 .
17. 已知 ,求 .18. 如图,点 是矩形 边 上的一点,点 , , 分别是 , , 的中点, ,则 的长为 .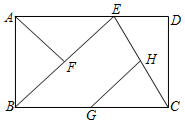 19. 若直线 与 的交点在第四象限,则 的取值范围为 .20. 如图,正方形 , , ,…按其所示放置,点 , , ,…和 , , ,…分别在直线 和 轴上,则点 的横坐标是 .
19. 若直线 与 的交点在第四象限,则 的取值范围为 .20. 如图,正方形 , , ,…按其所示放置,点 , , ,…和 , , ,…分别在直线 和 轴上,则点 的横坐标是 .
三、解答题
-
21. 计算: .22. 小聪、小明准备代表班级参加学校“党史知识”竞赛,班主任对这两名同学测试了6次,获得如下测试成绩折线统计图.根据图中信息,解答下列问题:
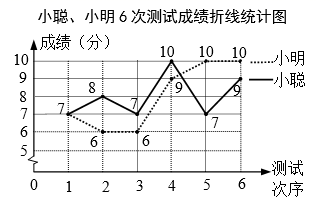 (1)、要评价每位同学成绩的平均水平,你选择什么统计量?求这个统计量.(2)、求小聪成绩的方差.(3)、现求得小明成绩的方差为 (单位:平方分).根据折线统计图及上面两小题的计算,你认为哪位同学的成绩较好?请简述理由.23. 如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)、要评价每位同学成绩的平均水平,你选择什么统计量?求这个统计量.(2)、求小聪成绩的方差.(3)、现求得小明成绩的方差为 (单位:平方分).根据折线统计图及上面两小题的计算,你认为哪位同学的成绩较好?请简述理由.23. 如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.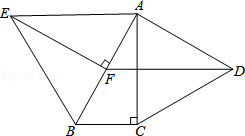 (1)、试说明AC=EF;(2)、求证:四边形ADFE是平行四边形.24. 如图,在平面直角坐标系中,一次函数 的图象经过点 ,与 轴相交于点 ,与 轴交于点 ,与正比例函数 的图象相交于点 ,点 的横坐标为1.
(1)、试说明AC=EF;(2)、求证:四边形ADFE是平行四边形.24. 如图,在平面直角坐标系中,一次函数 的图象经过点 ,与 轴相交于点 ,与 轴交于点 ,与正比例函数 的图象相交于点 ,点 的横坐标为1. (1)、求 , 的值;(2)、 为射线 上一点,过点 作 轴的平行线交 于点 ,当 时,求 点的坐标.25. 在学习函数的中,我们经历了列表、描点、连线画函数图象,并结合图象研究函数性质的过程.以下是我们研究函数 性质及其应用的部分过程,请按要求完成下列各小题.(1)、请把下表补充完整,并在图中补全该函数图象;
(1)、求 , 的值;(2)、 为射线 上一点,过点 作 轴的平行线交 于点 ,当 时,求 点的坐标.25. 在学习函数的中,我们经历了列表、描点、连线画函数图象,并结合图象研究函数性质的过程.以下是我们研究函数 性质及其应用的部分过程,请按要求完成下列各小题.(1)、请把下表补充完整,并在图中补全该函数图象;…
0
1
2
3
4
5
…
…
0
3
…
 (2)、根据函数图象,小明写出了该函数性质;
(2)、根据函数图象,小明写出了该函数性质;①该函数图象是轴对称图形,它的对称轴是 轴;
②该函数在自变量的取值范围内,有最大值和最小值.当 时,函数取得最大值3;当 时,函数取得最小值 ;
③该函数图象与坐标轴只有一个交点;
④当 或 时, 随 的增大而减小;当 时, 随 的增大而增大;其中正确的是(只写序号)
(3)、已知函数 的图象如图所示,结合你所画的函数图象,直接写出不等式 的解集(保留一位小数,误差不超过0.2)26. 已知在 中, 是 的中点, 是 延长线上的一点,连结 . (1)、如图1,若 ,求 的长.(2)、过点 作 ,交 延长线于点 ,如图2所示.若 ,求证: .(3)、如图3,若 ,是否存在实数 ,当 时, ?若存在,请直接写出 的值;若不存在,请说明理由.
(1)、如图1,若 ,求 的长.(2)、过点 作 ,交 延长线于点 ,如图2所示.若 ,求证: .(3)、如图3,若 ,是否存在实数 ,当 时, ?若存在,请直接写出 的值;若不存在,请说明理由.