山东省德州市德城区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-07-26 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中是最简二次根式的是（）

A、 $\sqrt{12}$ B、 $\sqrt{a^{2} + 1}$ C、 $\sqrt{\frac{1}{3}}$ D、 $\sqrt{3 a^{2}}$

查看试题解析
2. 以下运算错误的是（）

A、 $\sqrt{3 \times 5} = \sqrt{3} \times \sqrt{5}$ B、2 $\times \sqrt{2} = 2 \sqrt{2}$ C、 $\sqrt{16 + 9}$ = $\sqrt{16} + \sqrt{9}$ D、 $\sqrt{4 a^{2} b^{3}} = 2 a b \sqrt{b}$ （a＞0）

查看试题解析
3. 将直线y=2x向上平移两个单位，所得的直线是（）

A、y=2x+2 B、y=2x－2 C、y=2（x－2） D、y=2（x+2）

查看试题解析
4. 在2，5，3，7，2，6，2，1这组数据中插入一个任意数x，则一定不会改变的是（）

A、标准差 B、中位数 C、平均数 D、众数

查看试题解析
5. 如图，Rt△ABC中，∠ACB＝90°，若AB＝15cm，则正方形ADEC和正方形BCFG的面积之和为（）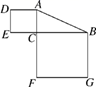

A、150cm² B、200cm² C、225cm² D、无法计算

查看试题解析
6. 下列图形中，表示一次函数y＝mx+n与正比例函数y＝mnx（m，n为常数，且mn≠0）的图象的是（）

A、 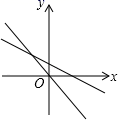B、 C、 D、

查看试题解析
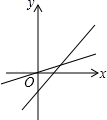7. 实数 $a$ 在数轴上的位置如图所示，则化简 $\sqrt{{(a - 4)}^{2}} + \sqrt{{(a - 11)}^{2}}$ 结果为（　　）

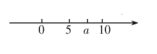A、7 B、-7 C、 $2 a - 15$ D、无法确定

查看试题解析
8. 下列条件之一能使菱形ABCD是正方形的为（　　）
①AC⊥BD ②∠BAD=90° ③AB=BC ④AC=BD．

A、①③ B、②③ C、②④ D、①②③

查看试题解析
9. 某射击选手10次射击成绩统计结果如下表，这10次成绩的众数、中位数分别是（）

成绩（环）

7

8

9

10

次数

1

4

3

2

A、8、8 B、8、8.5 C、8、9 D、8、10

查看试题解析
10. 如图，在 $△ A B C$ 中，点 $E$ 、 $D$ 、 $F$ 分别在边 $A B$ 、 $B C$ 、 $C A$ 上，且 $D E / / C A$ ， $D F / / B A$ ，下列四个判断中，错误的是（）

A、四边形 $A E D F$ 是平行四边形 B、如果 $A D = E F$ ，那么四边形 $A E D F$ 是矩形 C、如果 $A D$ 平分 $∠ E A F$ ，那么四边形 $A E D F$ 是菱形 D、如果AD⊥BC且AB＝AC，那么四边形AEDF是正方形

查看试题解析
11. 如图，小正方形边长为1，连接小正方形的三个顶点得 $Δ ABC$ ，则 $AC$ 边上的高是（）

A、 $\frac{3}{10} \sqrt{5}$ B、 $\frac{3}{2} \sqrt{2}$ C、 $\frac{4}{5} \sqrt{5}$ D、 $\frac{3}{5} \sqrt{5}$

查看试题解析
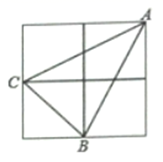12. 甲、乙两车从 $A$ 城出发匀速行驶至 $B$ 城.在整个行驶过程中，甲、乙两车离 $A$ 城的距离 $y$ (千米)与甲车行驶的时间 $t$ (小时)之间的函数关系如图所示.则下列结论：
① $A ， B$ 两城相距 $300$ 千米；②乙车比甲车晚出发 $1$ 小时，却早到 $1$ 小时；③乙车出发后 $2.5$ 小时追上甲车；④当甲、乙两车相距 $50$ 千米时， $t = \frac{5}{4} 或 \frac{15}{4}$ 其中正确的结论有（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析

二、填空题

13. 若|a-2|+ $\sqrt{b - 3}$ =0，则a²-2b=.

查看试题解析
14. 一个样本为1、3、2、2、a、b、c，已知这个样本的众数为 $3$ ，平均数为 $2$ ，则这个样本的方差为．

查看试题解析
15.
如图所示，每个小正方形的边长为1，A、B、C是小正方形的顶点，则∠ABC的度数为

查看试题解析
16. 如图，过矩形 $A B C D$ 的对角线 $B D$ 上一点 $K$ 分别作矩形两边的平行线 $M N$ 与 $P Q$ ，那么图中矩形 $A M K P$ 的面积 $S_{1}$ 与矩形 QCNK 的面积 $S_{2}$ 的大小关系是 $S_{1}$ $S_{2}$ ；（填“ $>$ ”或“ $<$ ”或“ $=$ ”）

查看试题解析
17. 如图，把直角三角形纸片折叠，使点C落在C′处，折痕为AD，得到∠CDC′＝60°.若∠ABC＝90°，AB＝1，AC＝ $\sqrt{10}$ ，则CD＝.

查看试题解析
18. 过点 $(5 ， 2)$ 的一条直线与 $x$ 轴、 $y$ 轴分别相交于点 $A$ 、 $B$ ，且与直线 $y = - \frac{3}{2} x + 1$ 平行，则在线段 $A B$ 上，横、纵坐标都是整数的点坐标是．

查看试题解析

三、解答题

19. 计算：

(1)、 $(\sqrt{24} + \sqrt{0.5}) - (2 \sqrt{\frac{1}{8}} - \sqrt{6})$

(2)、 ${(\sqrt{3} - 2)}^{2} - (4 \sqrt{2} - 8 \sqrt{6}) \div 2 \sqrt{2}$

查看试题解析
20. 如图，直线y=−x+10与x轴、y轴分别交于点B，C，点A的坐标为(8，0)，P(x，y)是直线y=−x+10在第一象限内一个动点.

(1)、求△OPA的面积S与x的函数关系式，并写出自变量x的取值范围；

(2)、当△OPA的面积为10时，求点P的坐标.

查看试题解析

21. 某校为了解七年级学生课外学习情况，随机抽取了部分学生作调查，通过调查将获得的数据按性别绘制成如下的女生频数分布表和如图所示的男生频数分布直方图：

女生频数分布表

学习时间t/分钟	人	占女生人数百分比
0≤t<30	4	20%
30≤t<60	m	15%
60≤t<90	5	25%
90≤t<120	6	n
120≤t<150	2	10%

根据图表解答下列问题：

(1)、在女生的频数分布表中，m＝， n＝．

(2)、此次调查共抽取了多少名学生？

(3)、此次抽样中，学习时间的中位数在哪个时间段？

(4)、求所调查学生课外学习近平均时间是多少分钟？

查看试题解析

22. 如图， $▱$ ABCD中，以A为圆心，DA的长为半径画弧，交BA于点F，作∠DAB的角平分线，交CD于点E，连接EF．

(1)、求证：四边形AFED是菱形；

(2)、若AD=4，∠DAB=60°，求四边形AFED的面积．

查看试题解析
23. 某果园计划新购进 $A ， B$ 两个品种的果树苗，若计划购进这两种果树苗共 $45$ 棵，其中A种苗的单价为 $7$ 元/棵，购买B种苗所需费用y(元）与购买数量x（棵）之间存在如图所示的函数关系．

(1)、当 $0 \leq x \leq 20$ 时，求y与x的函数关系式；

(2)、当 $20 < x \leq 45$ 时，求y与x的函数关系式；

(3)、若在购买计划中，B种苗的数量不少于 $22$ 棵但不超过 $35$ 棵，请设计购买方案，使总费用最低，并求出最低费用．

查看试题解析
24. 为降低空气污染，公交公司决定全部更换节能环保的燃气公交车．计划购买A型和B型两种公交车共10辆，其中每台的价格，年均载客量如表：

A型
B型
价格（万元/辆）
a
b
年均载客量（万人/年/辆）
60
100
若购买A型公交车1辆，B型公交车2辆，共需400万元；若购买A型公交车2辆，B型公交车1辆，共需350万元

(1)、求购买每辆A型公交车和每辆B型公交车分别多少万元？

(2)、如果该公司购买A型和B型公交车的总费用不超过1200万元，且确保这10辆公交车年均载客总和不少于680万人次，有哪几种购车方案？请你设计一个方案，使得购车总费用最少．

查看试题解析
25. 如图，在▱ABCD中，∠BCD的平分线交直线AD于点F，∠BAD的平分线交DC延长线于E，交线段BC于H点

(1)、证明：四边形AHCF是平行四边形；

(2)、证明：AF=EC；

(3)、若∠BAD=90°，G为CF的中点（如右图），判断△BEG的形状，并证明；

(4)、在（3）的条件上，若已知AB=6，BC=7，试求△BEG的面积．

查看试题解析

	A型	B型
价格（万元/辆）	a	b
年均载客量（万人/年/辆）	60	100

成绩（环）	7	8	9	10
次数	1	4	3	2