河北省石家庄市新华区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-07-26 类型:期末考试
一、单选题
-
1. 下列图形是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在平面直角坐标中,点M(-2,3)在( )
2. 在平面直角坐标中,点M(-2,3)在( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 如图,沿着虚线将四边形纸片剪成两部分,如果所得两个图形的内角和相等,则符合条件的剪法是( )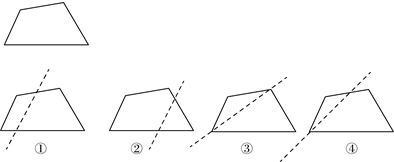 A、①② B、①③ C、②④ D、③④4. 下列调查不适合抽样调查的是( )A、市场上某种食品的某种添加剂的含量是否符合国家标准 B、检测某校八年级(1)班学生的视力情况 C、调查全市中学生一周的劳动时间 D、调查使用某品牌手机用户的满意度5. 在 中, 的值可能是( )A、 B、 C、 D、6. 关于函数 ,下列说法正确的是( )A、它的图像过点 B、 值随着 值的增大而增大 C、它的图像不经过第三象限 D、当 时,7. 如图,在菱形 中,对角线 , 相交于点 , 是 的中点,连接 ,若 ,则 的长是( )
A、①② B、①③ C、②④ D、③④4. 下列调查不适合抽样调查的是( )A、市场上某种食品的某种添加剂的含量是否符合国家标准 B、检测某校八年级(1)班学生的视力情况 C、调查全市中学生一周的劳动时间 D、调查使用某品牌手机用户的满意度5. 在 中, 的值可能是( )A、 B、 C、 D、6. 关于函数 ,下列说法正确的是( )A、它的图像过点 B、 值随着 值的增大而增大 C、它的图像不经过第三象限 D、当 时,7. 如图,在菱形 中,对角线 , 相交于点 , 是 的中点,连接 ,若 ,则 的长是( ) A、 B、 C、 D、8. 如图,直线 : 与一次函数 的图像相交于 ,则 ( )
A、 B、 C、 D、8. 如图,直线 : 与一次函数 的图像相交于 ,则 ( ) A、 B、 C、 D、9. 某班统计了该班全体学生 秒内高抬腿的次数,绘制频数分布表:
A、 B、 C、 D、9. 某班统计了该班全体学生 秒内高抬腿的次数,绘制频数分布表:次数
频数
给出以下结论:①组数是 ;②组距是 ;③全班有 名学生;④高抬腿次数在 范围内的学生占全班学生的 .其中正确结论的个数为( )
A、 B、 C、 D、10. 如图,在矩形 中, , ,将矩形沿 折叠使点 落在 处, 与 交于点 ,则 的值为( ) A、 B、 C、 D、11. 某公司为了激发员工工作的积极性,规定员工每天的薪金如下:生产的产品不超过 件,则每件 元,超过 件,超过的部分每件 元.下图是一名员工一天获得的薪金 (元)与其生产的产品件数 之间的函数关系图像,则下列结论错误的是( )
A、 B、 C、 D、11. 某公司为了激发员工工作的积极性,规定员工每天的薪金如下:生产的产品不超过 件,则每件 元,超过 件,超过的部分每件 元.下图是一名员工一天获得的薪金 (元)与其生产的产品件数 之间的函数关系图像,则下列结论错误的是( ) A、 B、 C、若该员工一天获得的薪金是 元,则其当天生产了 件产品 D、若该员工一天生产了 件产品,则其当天获得的薪金是 元12. 嘉嘉同学遇到这样一道题:“如图,正方形 中, 是对角线 上一点, 于点 , 于点 ,连接 , .”关于这道题有下列说法:①四边形 是矩形;② ;③ ;④ ,其中正确的说法是( )
A、 B、 C、若该员工一天获得的薪金是 元,则其当天生产了 件产品 D、若该员工一天生产了 件产品,则其当天获得的薪金是 元12. 嘉嘉同学遇到这样一道题:“如图,正方形 中, 是对角线 上一点, 于点 , 于点 ,连接 , .”关于这道题有下列说法:①四边形 是矩形;② ;③ ;④ ,其中正确的说法是( ) A、①②③ B、①②④ C、①③④ D、②③④
A、①②③ B、①②④ C、①③④ D、②③④二、填空题
-
13. 若正比例函数 的图像经过点 ,则k的值为 .14. 如图, 的对角线关于点 ,过点 的直线 交 边于点 ,交 边于点 ,已知 的面积为 ,则 .
 15. 琪琪同学沿着一条笔直的公路从 地出发到 地,已知 , 两地之间的距离为 ,她的平均速度为 ,若经过 ( ) 后琪琪与 地之间的距离为 ,则 与 之间的函数关系式为 .16. 如图,正五边形 的边 在直线 上,现将其绕点 按顺时针方向旋转一定角度,使五边形的边 的对应边 落在直线 上,则正五边形旋转的最小角度是°.
15. 琪琪同学沿着一条笔直的公路从 地出发到 地,已知 , 两地之间的距离为 ,她的平均速度为 ,若经过 ( ) 后琪琪与 地之间的距离为 ,则 与 之间的函数关系式为 .16. 如图,正五边形 的边 在直线 上,现将其绕点 按顺时针方向旋转一定角度,使五边形的边 的对应边 落在直线 上,则正五边形旋转的最小角度是°.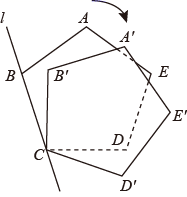 17. 已知一次函数 的图像与两坐标轴围成的三角形周长为 ,则 的值为 .18. 如图,点 是坐标原点,直线 : 与 轴交于点 ,以 为边向右构造正方形 ,使点 落在 轴上,延长 交直线 于点 ,再以 为边向右构造正方形 ,使点 落在 轴上,…,按此规律依次作正方形,则 所在直线的解析式为 .
17. 已知一次函数 的图像与两坐标轴围成的三角形周长为 ,则 的值为 .18. 如图,点 是坐标原点,直线 : 与 轴交于点 ,以 为边向右构造正方形 ,使点 落在 轴上,延长 交直线 于点 ,再以 为边向右构造正方形 ,使点 落在 轴上,…,按此规律依次作正方形,则 所在直线的解析式为 .
三、解答题
-
19. 已知点 ,根据下列条件,求出点 的坐标.(1)、点 在 轴上;(2)、点 的坐标为 ,直线 轴.20. 如图,在四边形 中, , 分别为 , 上的点,且 ,连接 , ,若四边形 是平行四边形.求证:四边形 是平行四边形.
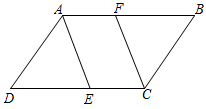 21. 一个正多边形的周长为 ,边长为 ,一个外角为 .(1)、若 ,求 的值;(2)、若 ,求 的值.22. 如图,在平面直角坐标系中,已知 , , .
21. 一个正多边形的周长为 ,边长为 ,一个外角为 .(1)、若 ,求 的值;(2)、若 ,求 的值.22. 如图,在平面直角坐标系中,已知 , , . (1)、画出 关于 轴对称的 ;(2)、画出 向下平移 个单位长度得到 ;(3)、在 的内部有一点 ,其坐标为 ,请直接写出点 经过以上变换后的对应点 的坐标.23. 如图,在平面直角坐标系中, 是坐标原点,已知点 , , ,直线 : ( ).
(1)、画出 关于 轴对称的 ;(2)、画出 向下平移 个单位长度得到 ;(3)、在 的内部有一点 ,其坐标为 ,请直接写出点 经过以上变换后的对应点 的坐标.23. 如图,在平面直角坐标系中, 是坐标原点,已知点 , , ,直线 : ( ). (1)、求直线 的解析式;(2)、若直线 经过点 .
(1)、求直线 的解析式;(2)、若直线 经过点 .①当 时,求 的值;
②若直线 与线段 有交点,直接写出 的取值范围.
24. 为了解全校学生课外阅读情况,该校随机调查了部分学生在一周内借阅图书的次数,并制成如下不完成的扇形统计图的和条形统计图,请你根据统计图中的信息,解答下列问题.
 (1)、求本次调查的人数;(2)、求 , 的值;(3)、求本次调查中,在一周内借阅图书不少于 次的人数所占百分比.25. 某文具商店计划用不超过 元的资金购买书包和计算器共 个,已知书包和计算器的进价与售价如表.设购买书包 个(其中 ),购买书包的费用为 元,购买计算器的费用为 元.
(1)、求本次调查的人数;(2)、求 , 的值;(3)、求本次调查中,在一周内借阅图书不少于 次的人数所占百分比.25. 某文具商店计划用不超过 元的资金购买书包和计算器共 个,已知书包和计算器的进价与售价如表.设购买书包 个(其中 ),购买书包的费用为 元,购买计算器的费用为 元.每件商品
进价(元)
售价(元)
书包
计算器
(1)、当 时, , ;(2)、求最多能购买多少个书包;(3)、设售出这批书包和计算器共盈利 元,求 与 之间的函数关系式;文具店购进多少个书包时,才能获得最大利润?最大利润是多少?26. 如图,在平面直角坐标系中, 为坐标原点,四边形 为矩形, , .点 是 的中点,动点 在线段 上以每秒 个单位长度的速度由点 向点 运动(到点 时停止).设动点 的运动时间为 秒.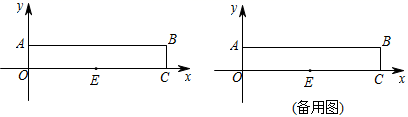 (1)、当 为何值时,四边形 是平行四边形?(2)、若四边形 是平行四边形,请判断四边形 的形状,并说明理由;(3)、在线段 上是否存在一点 ,使得以 , , , 为顶点的四边形是菱形?若存在,求出 的值;若不存在,请说明理由.
(1)、当 为何值时,四边形 是平行四边形?(2)、若四边形 是平行四边形,请判断四边形 的形状,并说明理由;(3)、在线段 上是否存在一点 ,使得以 , , , 为顶点的四边形是菱形?若存在,求出 的值;若不存在,请说明理由.