北京市延庆区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-07-26 类型:期末考试
一、单选题
-
1. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、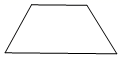 D、
D、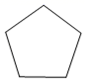 2. 一个多边形的内角和为540°,则这个多边形的边数是( )A、4 B、6 C、5 D、73. 某小区2019年屋顶绿化面积为2000平方米,计划2021年屋顶绿化面积要达到2880平方米.若设屋顶绿化面积的年平均增长率为x,则依题意所列方程正确的是( )A、2000(1+x)2=2880 B、2000(1﹣x)2=2880 C、2000(1+2x)=2880 D、2000x2=28804. 如图,菱形ABCD的一边中点M到对角线交点O的距离为3cm,则菱形ABCD周长为( )
2. 一个多边形的内角和为540°,则这个多边形的边数是( )A、4 B、6 C、5 D、73. 某小区2019年屋顶绿化面积为2000平方米,计划2021年屋顶绿化面积要达到2880平方米.若设屋顶绿化面积的年平均增长率为x,则依题意所列方程正确的是( )A、2000(1+x)2=2880 B、2000(1﹣x)2=2880 C、2000(1+2x)=2880 D、2000x2=28804. 如图,菱形ABCD的一边中点M到对角线交点O的距离为3cm,则菱形ABCD周长为( )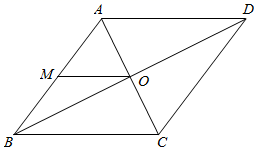 A、10cm B、12cm C、16 cm D、24 cm5. 已知关于x的一元二次方程 的一个根是0,则m的值为( )A、1 B、0 C、-1 D、1或-16. 若菱形ABCD的对角线AC=4,BD=6,则该菱形的面积为( )A、24 B、6 C、12 D、57. 矩形具有而平行四边形不具有的性质是( )A、对角线互相平分 B、对角线相等 C、对角线互相垂直 D、四边相等8. 图(1)是饮水机的图片.打开出水口,饮水桶中水面由图(1)下降到图(3)的位置的过程中,如果水减少的体积是y,水面下降的高度是x,那么能够表示y与x之间函数关系的图象可能是( )
A、10cm B、12cm C、16 cm D、24 cm5. 已知关于x的一元二次方程 的一个根是0,则m的值为( )A、1 B、0 C、-1 D、1或-16. 若菱形ABCD的对角线AC=4,BD=6,则该菱形的面积为( )A、24 B、6 C、12 D、57. 矩形具有而平行四边形不具有的性质是( )A、对角线互相平分 B、对角线相等 C、对角线互相垂直 D、四边相等8. 图(1)是饮水机的图片.打开出水口,饮水桶中水面由图(1)下降到图(3)的位置的过程中,如果水减少的体积是y,水面下降的高度是x,那么能够表示y与x之间函数关系的图象可能是( ) A、
A、 B、
B、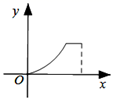 C、
C、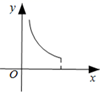 D、
D、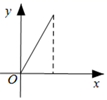
二、填空题
-
9. 函数y= 中自变量x的取值范围是 .10. 一元二次方程x2﹣2x=0的解是 .
11. 判断一元二次方程x2﹣4mx+4m2=0的根的情况是 .12. 下图是由射线AB,BC,CD,DE,EA组成的平面图形,则∠1+∠2+∠3+∠4+∠5=.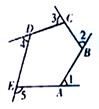 13. 已知P1(﹣3,y1)、P2(2,y2)是一次函数y=2x+1图象上的两个点,则y1y2(填“>”、“<”或“=”).14. 下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
13. 已知P1(﹣3,y1)、P2(2,y2)是一次函数y=2x+1图象上的两个点,则y1y2(填“>”、“<”或“=”).14. 下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:甲
乙
丙
丁
平均数(cm)
183
183
182
182
方差
5.7
3.5
6.7
8.6
要从中选择一名发挥稳定的运动员去参加比赛,应该选择 .
15. 《算学宝鉴》中记载了我国南宋数学家杨辉提出的一个问题:“直田积八百六十四步,之云阔不及长一十二步,问阔及长各几步?”译文:“一个矩形田地的面积等于864平方步,且它的宽比长少12步,问长与宽各是几步?”若设矩形田地的长为x步,则可列方程为 .16. 如图,正方形ABCD的边长为4,E为AB边的中点,点F在BC边上移动,点B关于直线EF的对称点记为B',连接B'D,B'E,B'F.当四边形BEB'F为正方形时,B'D的长为 .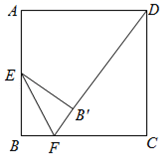
三、解答题
-
17. 选择适当的方法解下列一元二次方程.(1)、x2=9(2)、x2+2x+1=0(3)、x2+4x﹣5=0(4)、2x2﹣3x﹣1=018. 已知:一次函数y=kx+b(k≠0)的图象经过A(2,3)和点B(0,﹣1).(1)、求这个一次函数的表达式;(2)、判断点P(2,1)是否在这个一次函数y=kx+b(k≠0)的图象上.19. 已知:如图,四边形ABCD是平行四边形,AE⊥BC,AF⊥CD,垂足分别是E,F,且BE=DF.
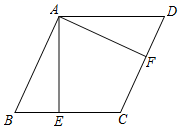 (1)、求证:△ABE≌△ADF;(2)、求证:四边形ABCD是菱形.20. 已知关于x的一元二次方程 有两个不相等的实数根,求m的取值范围.21. 如图,将矩形ABCD沿对角线BD所在直线折叠,点C落在同一平面内,落点记为F,BF与AD交于点E,若AB=4,BC=8,求BE的长.
(1)、求证:△ABE≌△ADF;(2)、求证:四边形ABCD是菱形.20. 已知关于x的一元二次方程 有两个不相等的实数根,求m的取值范围.21. 如图,将矩形ABCD沿对角线BD所在直线折叠,点C落在同一平面内,落点记为F,BF与AD交于点E,若AB=4,BC=8,求BE的长. 22. 下面是小明设计的“在一个矩形内作正方形”的尺规作图过程.
22. 下面是小明设计的“在一个矩形内作正方形”的尺规作图过程.已知:如图,四边形ABCD是矩形.
求作:正方形ABEF(点E在BC上,点F在AD上).
作法:①以A为圆心,AB长为半径作弧,交AD于点F;
②以B为圆心,AB长为半径作弧,交BC于点E;
③连接EF.
四边形ABEF就是所求作的正方形.
根据小明设计的尺规作图过程,
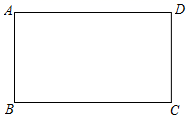 (1)、使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)、完成下面的证明.
(1)、使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)、完成下面的证明.证明:∵AF=AB,BE=AB
∴ ▲ = ▲ .
∵矩形ABCD中,AD∥BC,
∴AF∥BE.
∴四边形ABEF为平行四边形.( ▲ )(填推理的依据)
∵四边形ABCD是矩形,
∴∠A=90°.
∴四边形ABEF为矩形.( ▲ )(填推理的依据)
∵AF=AB,
∴四边形ABEF为正方形.( ▲ )(填推理的依据)
23. 在同一平面直角坐标系中画出正比例函数y=x和一次函数y=﹣x+2的图象,并求出这两个函数图象与x轴围成的三角形面积.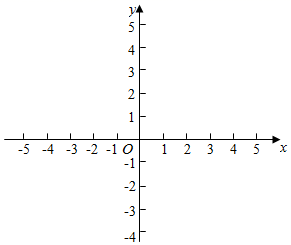 24. 有一块长12cm,宽8cm的长方形铁皮,如果在铁皮的四个角上截去四个相同的小正方形,然后把四边折起来,做成一个底面面积为32cm2的无盖的盒子,求截去的小正方形的边长.
24. 有一块长12cm,宽8cm的长方形铁皮,如果在铁皮的四个角上截去四个相同的小正方形,然后把四边折起来,做成一个底面面积为32cm2的无盖的盒子,求截去的小正方形的边长.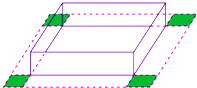 25. 为庆祝中国共产党成立100周年,某中学举行了主题为“奋斗百年路,启航新征程”诗歌朗诵比赛,共有100名学生参加.为了更好地了解本次比赛成绩分布情况,随机抽取了其中若干名学生的成绩作为样本,列出的频数分布表与绘制的频数分布直方图的一部分如下(除最后一组外,每组分数段中的分数包括最低分,不包括最高分):
25. 为庆祝中国共产党成立100周年,某中学举行了主题为“奋斗百年路,启航新征程”诗歌朗诵比赛,共有100名学生参加.为了更好地了解本次比赛成绩分布情况,随机抽取了其中若干名学生的成绩作为样本,列出的频数分布表与绘制的频数分布直方图的一部分如下(除最后一组外,每组分数段中的分数包括最低分,不包括最高分):样本成绩频数分布表
分组/分
频数
频率
50≤x<60
6
0.12
60≤x<70
a
0.28
70≤x<80
16
0.32
80≤x<90
10
0.20
90≤x≤100
c
b
合计
50
1.00
请根据所给信息,解答下列问题:
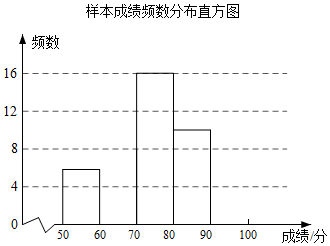 (1)、表中的a= , b= , c=;(2)、把上面的频数分布直方图补充完整;(3)、如果成绩达到80及80分以上者为优秀,那么请你根据抽取的样本数据,估计该校参加比赛的100名学生中成绩优秀的有多少名.26. 在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象是由函数y=2x的图象平移得到,且经过点(1,3).(1)、求这个一次函数的表达式;(2)、当x>1时,对于x的每一个值,函数y=mx(m≠0)的值大于一次函数y=kx+b(k≠0)的值,直接写出m的取值范围.27. 如图,在正方形ABCD中,点E在AB边上,连接DE,点F在边BC的延长线上,且CF=AE,连接DF,EF,取EF中点G,连接DG并延长交BC于H,连接BG,且∠EGB=45°.
(1)、表中的a= , b= , c=;(2)、把上面的频数分布直方图补充完整;(3)、如果成绩达到80及80分以上者为优秀,那么请你根据抽取的样本数据,估计该校参加比赛的100名学生中成绩优秀的有多少名.26. 在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象是由函数y=2x的图象平移得到,且经过点(1,3).(1)、求这个一次函数的表达式;(2)、当x>1时,对于x的每一个值,函数y=mx(m≠0)的值大于一次函数y=kx+b(k≠0)的值,直接写出m的取值范围.27. 如图,在正方形ABCD中,点E在AB边上,连接DE,点F在边BC的延长线上,且CF=AE,连接DF,EF,取EF中点G,连接DG并延长交BC于H,连接BG,且∠EGB=45°. (1)、依题意,补全图形;(2)、求证:DE⊥DF;(3)、用等式表示线段BG,GH与EF之间的数量关系,并证明.28. 在平面直角坐标系xOy中,点P的坐标为(x1 , y1),点Q的坐标为(x2 , y2),且x1≠x2 , y1≠y2 , 若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“合成矩形”.如图为点P,Q的“合成矩形”的示意图.
(1)、依题意,补全图形;(2)、求证:DE⊥DF;(3)、用等式表示线段BG,GH与EF之间的数量关系,并证明.28. 在平面直角坐标系xOy中,点P的坐标为(x1 , y1),点Q的坐标为(x2 , y2),且x1≠x2 , y1≠y2 , 若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“合成矩形”.如图为点P,Q的“合成矩形”的示意图. (1)、若A点坐标为(2,0),
(1)、若A点坐标为(2,0),①当B点坐标为(5,1)时,点A,B的“合成矩形”的面积是 ▲ ;
②若点C在直线x=4上,且点A,C的“合成矩形”为正方形,求直线AC的表达式;
③若点P在直线y=﹣2x+2上,且点A,P的“合成矩形”为正方形,直接写出P点的坐标;
(2)、点O的坐标为(0,0),点D为直线y=x+b(b≠0)上一动点,若O,D的“合成矩形”为正方形,且此正方形面积不小于2时,求b的取值范围.