北京市门头沟区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-07-26 类型：期末考试

进入出卷网下载

一、单选题

1. 如果点 $P$ 的坐标是 $(3 ， 1)$ ，那么点 $P$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 篆体是我国汉字古代书体之一．下列篆体字“美”，“丽”，“北”，“京”中，不是轴对称图形的为（）

A、 B、 C、 D、

查看试题解析
3. 如果一个多边形的内角和为 $540 °$ ，那么这个多边形的边数是（）

A、 $6$ B、 $5$ C、 $4$ D、 $3$

查看试题解析
4. 如果函数 $y = (2 k - 6) x + 5$ 是关于 $x$ 的一次函数，且 $y$ 随 $x$ 增大而增大，那么 $k$ 取值范围是（）

A、 $k \neq 0$ B、 $k < 3$ C、 $k \neq 3$ D、 $k > 3$

查看试题解析
5. 将方程 $x^{2} + 2 x - 5 = 0$ 配方后，原方程变形为（）

A、 ${(x + 2)}^{2} = 9$ B、 ${(x - 2)}^{2} = 9$ C、 ${(x + 1)}^{2} = 6$ D、 ${(x - 1)}^{2} = 6$

查看试题解析
6. 下列命题正确的是（）．

A、一组对边平行，另一组对边相等的四边形是平行四边形 B、对角线相等的四边形是矩形 C、有一组邻边相等的四边形是菱形 D、有一组邻边相等且有一个角是直角的平行四边形是正方形

查看试题解析
7. 某地为发展教育事业，加强了对教育经费的投入，2020年投入 $4000$ 万元，预计2022年投入 $6000$ 万元，设教育经费的年平均增长率为 $x ，$ 下面所列方程正确的是（）

A、 $4000 {(1 + x)}^{2} = 6000$ B、 $400 x^{2} = 6000$ C、 $4000 {(1 + x %)}^{2} = 6000$ D、 $4000 (1 + x) + 4000 {(1 + x)}^{2} = 6000$

查看试题解析
8. 某公司新产品上市30天全部售完．图1表示产品的市场日销售量与上市时间之间的关系，图2表示单件产品的销售利润与上市时间之间的关系，下列四个结论中错误的是（）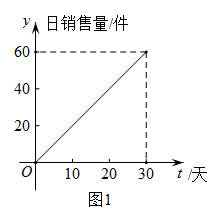

A、第30天该产品的市场日销售量最大 B、第20天至30天该产品的单件产品的销售利润最大 C、第20天该产品的日销售总利润最大 D、第20天至30天该产品的日销售总利润逐日增多

查看试题解析

二、填空题

9. 一元二次方程 $3 x^{2} - 6 x - 7 = 0$ 的二次项系数是，常数项是．

查看试题解析
10. 在函数y= $\sqrt{2 x - 1}$ 中，自变量x的取值范围是．

查看试题解析
11. 点 $P (2 ， 1)$ 关于 $x$ 轴对称点的坐标为．

查看试题解析
12. 请写出一个图象经过点 $(1, 1)$ 的一次函数的表达式：．

查看试题解析
13. 在菱形ABCD中，对角线AC与BD交于点O，如果∠ABC＝60°，AC＝4，那么这个菱形的面积是．

查看试题解析
14. 有两名学员小林和小明练习射击，第一轮10枪打完后两人打靶的环数如图所示，通常新手的成绩不太稳定，那么根据图中的信息，估计小林和小明两人中新手是．

查看试题解析
15. 写出一个一元二次方程，使其两个根中有一个根为 $2$ ，此方程为．

查看试题解析
16. 在平面直角坐标系 $x O y$ 中， $A (0 ， 1) ， B (1 ， 1)$ ，下面有四种说法：
①一次函数 $y = \frac{1}{2} x$ 的图象与线段 $A B$ 有公共点；

②当 $0 \leq b \leq 1$ 时，一次函数 $y = x + b$ 的图象与线段 $A B$ 有公共点；

③当 $k < 2 ， k \neq 0$ 时，一次函数 $y = k x - 1$ 的图象与线段 $A B$ 有公共点；

④当 $\frac{1}{2} \leq k \leq 1$ 时，一次函数 $y = k x + k$ 的图象与线段 $A B$ 有公共点．

上述说法中正确的是（填序号）．

查看试题解析

三、解答题

17. 解方程： $2 x (x + 3) = x^{2} + 8 x$ ．

查看试题解析
18. 已知：如图， $E ， F$ 是平行四边形 $A B C D$ 对角线 $B D$ 上的两点，且 $B E = D F$ ．
求证： $A E = C F$ ．

查看试题解析
19. 阅读材料，并回答问题：
小明在学习一元二次方程时，解方程 $2 x^{2} - 8 x + 3 = 0$ 的过程如下：

解： $2 x^{2} - 8 x + 3 = 0$ ．

$2 x^{2} - 8 x = - 3 ，$ ①

$x^{2} - 4 x = - \frac{3}{2} ，$ ②

$x^{2} - 4 x + 4 = - \frac{3}{2} + 4 ，$ ③

${(x - 2)}^{2} = \frac{5}{2} ，$ ④

$x - 2 = \frac{\sqrt{10}}{2} ，$ ⑤

$x = 2 + \frac{\sqrt{10}}{2} ．$ ⑥

问题：

(1)、上述过程中，从第步开始出现了错误（填序号）；

(2)、发生错误的原因是：；

(3)、在下面的空白处，写出正确的解答过程．

查看试题解析
20. 如图，在平行四边形 ABCD 中，过点 D 作 DE ^ AB 于点 E ，点 F在边 CD 上， DF = BE ，连接 AF ， BF ．

(1)、求证：四边形 BFDE 是矩形；

(2)、若 AF 平分 ∠DAB ， CF=3，BF=4 ，求 DF 长．

查看试题解析
21. 已知：如图1，线段 $a ，$ 线段 $b$ ．
求作：菱形 $A B C D ，$ 使其两条对角线的长分别等于线段 $a ， b$ 的长．

作法：①如图1，作线段 $b$ 的垂直平分线 $c$ ，交线段 $b$ 于点 $E$ ；

②如图2，作射线 $m$ ，在 $m$ 上截取线段 $A C = a$ ；

③作线段 $A C$ 的垂直平分线 $G F$ 交线段 $A C$ 于点 $O$ ；

④以点 $O$ 为圆心，线段 $b$ 的一半为半径作弧，交直线 $G F$ 于点 $B ， D$ ；

⑤连接 $A B ， B C ， C D ， D A$ ．

$∵$ 四边形 $A B C D$ 就是所求作的菱形．

问题：

(1)、使用直尺和圆规，依作法补全图2（保留作图痕迹）；

(2)、完成下面的证明．
证明： $∵ O A = O C ， O B = O D$ ，

$∵$ 四边形 $A B C D$ 是_

$∵ A C ⊥ B D ，$

$∴$ 四边形 $A B C D$ 是菱形．（）（填推理的依据）．

查看试题解析
22. 如图，将长方形纸片 $A B C D$ 沿对角线 $A C$ 折叠，点 $D$ 落在点 $F$ 处， $A F$ 与 $B C$ 相交于点 $E$ ．

(1)、求证： $△ A B E ≌ △ C F E$ ；

(2)、若 $A B = 4$ ， $A D = 8$ ，求 $A E$ 的长．

查看试题解析
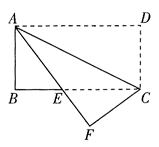23. 已知关于 $x$ 的一元二次方程 $x^{2} + 2 x + 2 k - 4 = 0$ 有两个不相等的实数根

(1)、求 $k$ 的取值范围；

(2)、若 $k$ 为正整数，且该方程的根都是整数，求 $k$ 的值。

查看试题解析
24. 在平面直角坐标系 $x O y$ 中，一次函数 $y = k x + b (k \neq 0)$ 的图象由函数 $y = x$ 的图象平移得到，且经过点(1，2)．

(1)、求这个一次函数的解析式；

(2)、当 $x > 1$ 时，对于 $x$ 的每一个值，函数 $y = m x (m \neq 0)$ 的值大于一次函数 $y = k x + b$ 的值，直接写出 $m$ 的取值范围．

查看试题解析

25. 为了弘扬中华传统文化，了解学生的整体阅读能力，某校组织全校学生进行了一次阅读理解测试．从中随机抽取了八年级（1）班和八年级（2）班各

25

人的成绩（单位：分）进行了统计分析．

a．收集数据

⑴班 $77 79 80 80 85 86 86 87 88 89 89 90 91$

$91 91 91 91 92 93 95 95 96 97 98 98$

⑵班 $69 79 79 79 86 87 87 89 89 90 90 90 90$

$90 91 92 92 92 94 95 96 96 97 98 98$

b．整理和描述数据

成绩 $x /$ 分数	⑴班		⑵班
成绩 $x /$ 分数	频数	频率	频数	频率
$60 \leq x < 70$	$0$	$0$	$1$	$0.04$
$70 \leq x < 80$	$2$	$0.08$	$3$	$0.12$
$80 \leq x < 90$	$9$	$a$	$5$	$0.20$
$90 \leq x \leq 100$	$14$		$16$	$0.64$

注：成绩 $90$ 分及以上为优秀， $80 ~ 89$ 分为合格， $80$ 分以下为不合格．

c．分析数据

两组样本数据的平均数､中位数､众数如下表所示：

班级	平均数	众数	中位数
⑴班	$89.4$	$b$	$91$
⑵班	$89.4$	$90$	$c$

根据以上信息，回答下列问题：

(1)、表中

a =

，

b =

，

c =

﹔

(2)、在抽取的两班中，测试成绩比较整齐的是班（填“1”或“2”）；

(3)、根据调查情况，可以推断班本次测试成绩较好，理由为．

查看试题解析

26. 在平面直角坐标系 $x O y$ 中，直线 $l_{1} ： y = k x + b$ 经过 $A (4 ， 1)$ 和 $B (7 ， 2)$ 两点．

(1)、求直线的表达式；

(2)、如果横、纵坐标都是整数的点叫作整点，直线 $l_{2}$ 和直线 $l_{1}$ 关于 $x$ 轴对称，过点 $C (m ， 0)$ 作垂直于 $x$ 轴的直线 $l_{3} ， l_{5}$ 与 $l_{1}$ 和 $l_{2}$ 的区域为“ $W$ ”（不包含边界）．
①当 $m = 3$ 时，求区域“ $W$ ”内整点的个数；

②如果区域“ $W$ ”内恰好有 $6$ 个整点，直接写出 $m$ 的取值范围．

查看试题解析
27. 已知，在正方形 $A B C D$ 中，连接对角线 $B D$ ，点 $E$ 为射线 $C B$ 上一点，连接 $A E ， F$ 是 $A E$ 的中点，过点 $F$ 作 $F M ⊥ A E$ 于 $F ， F M$ 交直线 $B D$ 于 $M$ ，连接 $M E 、 M C$ ．

(1)、如图1，当点 $E$ 在 $C B$ 边上时
①依题意补全图1；

②猜想 $∠ M E C$ 与 $∠ M C E$ 之间的数量关系，并证明．

(2)、如图2，当点 $E$ 在 $C B$ 边的延长线上时，补全图2，并直接写出 $∠ M E C$ 与 $∠ M C E$ 之间的数量关系．

查看试题解析
28. 在平面直角坐标系 $x O y$ 中，对于 $P (a ， b)$ 和 $Q (a ， b')$ 给出如下定义：
如果 $b' = {\begin{array}{l} b ， a \geq 1 \\ - b ， a < 1 \end{array}$ ，那么点 $Q$ 就是点 $P$ 的关联点．

例如，点 $(2 ， 4)$ 的关联点是 $(2 ， 4)$ ，点 $(- 1 ， 4)$ 的关联点是 $(- 1 ， - 4)$ ．

(1)、点 $(\sqrt{2} ， 1)$ 的关联点是，点 $(- 5 ， 1)$ 的关联点是．

(2)、如果点 $A (- 1 ， - 2)$ 和点 $B (- 1 ， 2)$ 中有一个点是直线 $y = 2 x$ 上某一个点的关联点，那么这个点是．

(3)、如果点 $P$ 在直线 $y = - x + 3 (- 2 \leq x \leq k ， k > - 2)$ 上，其关联点 $Q$ 的纵坐标 $b'$ 的取值范围是 $- 5 \leq b' \leq 2$ ，求 $k$ 的取值范围．

查看试题解析