初中数学北师大版八年级上学期 第一章 1.3 勾股定理的应用
试卷更新日期：2021-07-25 类型：同步测试
一、单选题
-
1. 用梯子登上20m高的建筑物，为了安全要使梯子的底面距离建筑物15m，至少需要（ ）m长的梯子.A、20 B、25 C、15 D、52. 在直角坐标系中，点P（﹣2，3）到原点的距离是（ ）A、 B、3 C、2 D、3. 如图，为了求出湖两岸A、B两点之间的距离，观测者从测点A、B分别测得 ，又量得 ， ，则A、B两点之间的距离为（ ）
A、10m B、 C、12m D、13m4. 在《算法统宗》中有一道“荡秋千”的问题：“平地秋千未起，踏板一尺离地 送行二步与人齐，五尺人高曾记. 仕女佳人争蹴，终朝笑语欢嬉.良工高士素好奇，算出索长有几.”此问题可理解为：如图，有一架秋千，当它静止时，踏板离地距离 长度为1尺.将它往前水平推送10尺时，即 ＝10尺，则此时秋千的踏板离地距离 就和身高5尺的人一样高.若运动过程中秋千的绳索始终拉得很直，则绳索 长为（ ）
A、13.5尺 B、14尺 C、14.5尺 D、15尺5. 勾股定理是人类最伟大的科学发现之一，在我国古代《周髀算经》中早有记载。如图①，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图②的方式放置在最大正方形内。若图中阴影部分图形的面积为3，则较小两个正方形重叠部分图形的面积为（ ）
A、1 B、2 C、3 D、46. 如图是一个圆柱形饮料罐，底面半径是5，高是12，上底面中心有一个小圆孔，则一条到达底部的直吸管在罐内部分a的长度x（罐壁厚度和小圆孔大小忽略不计）范围是（ ）
A、12≤x≤13 B、12≤x≤15 C、5≤x≤12 D、5≤x≤137. 等腰三角形一腰长为5，这一腰上的高为3，则这个等腰三角形底边长为（ ）A、 B、 C、 或 D、4或8. 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案，已知大正方形面积为49，小正方形面积为4，若用 、 表示直角三角形的两直角边 ，下列四个说法：① ，② ，③ ，④ ．其中说法正确的是（ ）
A、①③ B、①②③ C、①②④ D、①②③④二、填空题
-
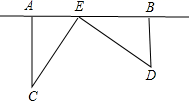
9. 下图是公园的一角，有人为了抄近道而避开横平竖直的路的拐角 ，而走“捷径 ”，于是在草坪内走出了一条不该有的“路 ”.已知 米， 米，只为少走米的路.
10. 如图，将两个边长为1的小正方形，沿对角线剪开，重新拼成一个大正方形，则大正方形的边长是.
11. 如图，从电线杆离地面3米处向地面拉一条长为5米的拉线，这条拉线在地面的固定点距离电线杆底部有米.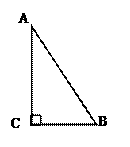
12. 如图，在平面直角坐标系xOy中，矩形ABCD的边AB在x轴上，AO=2，BO=3，BC=4.将正方形沿箭头方向推，使点D落在y轴正半轴上点D’处，则点C的对应点C’的坐标为.
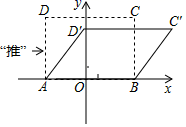13. 有一根长33厘米的木棒（粗细忽略），木箱的长、宽、高分别为24厘米、18厘米、16厘米，这根木棒理论上（填“能”或“不能”）放进木箱.14. 如图所示，一棵9m高的树被风刮断了，树顶落在离树根6m处，则折断处的高度AB为.
15. 如图是学校艺术馆中的柱子，高4.5m ． 为迎接艺术节的到来，工作人员用一条花带从柱底向柱顶均匀地缠绕3圈，一直缠到起点的正上方为止．若柱子的底面周长是2m ， 则这条花带至少需要m ．
16. 如图：知：AM⊥MN，BN⊥MN，垂足分别为M，N，点C是MN上使AC+BC的值最小的点．若AM=3，BN=5，MN=15，则AC+BC= ．
三、解答题
-
17. 某快递公司为了给客户提供“安全、快速”的优质服务，购置了一台无人机往返A，B，C三地运输货物，如图所示，幸福小区C位于快递站点B的北偏东35°方向，沁苑小区A位于快递站点B的南偏东55°方向，无人机以1千米/分钟的速度配送快递时，从B到C需飞行8分钟，从B到A需飞行15分钟．请求出无人机从幸福小区C与沁苑小区A之间所需要的时间。
