初中数学北师大版九年级上学期第二章 2.2 配方法求解一元二次方程

试卷更新日期：2021-07-25 类型：同步测试

进入出卷网下载

1. 用配方法解方程x²﹣4x＝1时，原方程应变形为（）

A、（x﹣2）²＝1 B、（x+2）²＝5 C、（x+2）²＝1 D、（x﹣2）²＝5

查看试题解析
2. 用配方法将方程 x²- 4x-2= 0 变形为（x- 2）²=m 的过程中， m的值是（）

A、7 B、6 C、5 D、4

查看试题解析
3. 将一元二次方程2x²﹣6x+1＝0配方，得（x+h）²＝k，则h、k的值分别为（）

A、3、8 B、﹣3、8 C、 $\frac{3}{2}$ 、 $\frac{7}{4}$ D、 $- \frac{3}{2}$ 、 $\frac{7}{4}$

查看试题解析
4. 已知方程x²-6x+q=0可以配方成（x-p）²=7的形式，那么q的值是

A、9 B、3 C、2 D、-2

查看试题解析
5. 若方程x²﹣8x+m＝0可通过配方写成（x﹣n）²＝6的形式，则x²+8x+m＝5可配方成（）

A、（x﹣n+5）²＝1 B、（x+n）²＝1 C、（x﹣n+5）²＝11 D、（x+n）²＝11

查看试题解析
6. 用配方法解下列方程时，配方有错误的是（）．

A、x²-2x-99=0化为(x-1)²=100 B、x²+8x+9=0化为(x+4)²=25 C、2t²-7t-4=0化为 ${(t - \frac{7}{4})}^{2} = \frac{81}{16}$ D、3y²-4y-2=0化为 ${(y - \frac{2}{3})}^{2} = \frac{10}{9}$

查看试题解析
7. 下列用配方法解方程 $\frac{1}{2} x^{2} - x - 2 = 0$ 的四个步骤中，出现错误的是（）

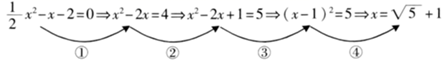A、① B、② C、③ D、④

查看试题解析
8.
把一元二次方程 $x^{2} + 6 x + 4 = 0$ 化成 $(x + m)^{2} = n$ 的形式，则 $m + n$ 的值（）

A、3 B、5 C、6 D、8

查看试题解析

9. 用配方法解方程 $x^{2} - 2 x - 5 = 0$ 时，将方程化为 ${(x - m)}^{2} = n$ 的形式，则m= ， n= ．

查看试题解析
10. 已知： $x^{2} - 3 x - 1 = 0$ ，则 $x - \frac{1}{x}$ = ．

查看试题解析
11. 已知实数满足 $4 x^{2} - 4 x + 1 = 0$ ，则代数式 $2 x + \frac{1}{2 x}$ 的值为．

查看试题解析
12. 将一元二次方程x²-8x-5=0化成 $（ x + a)^{2} = b$ 的形式，则 $3 a - b$ = ．

查看试题解析
13. 当 $x =$ 时，代数式 $x^{2} - x$ 与 $x - 1$ 的值相等.

查看试题解析
14. 将一元二次方程 $a x^{2} + b x + c = 0$ ，化为 ${(x - m)}^{2}$ = $\frac{b^{2} - 4 a c}{4 a^{2}}$ ，则m为．

查看试题解析
15. 用配方法解方程 $\frac{1}{2} x^{2} + x - \frac{5}{2} = 0$ 时，可配方为 $\frac{1}{2} [{(x + 1)}^{2} + k] = 0$ ，其中 $k =$ .

查看试题解析
16. 已知x，y，z为实数，且2x﹣3y+z=3，则x²+（y﹣1）²+z²的最小值为．

查看试题解析

19. 已知 $y_{1} = \frac{1}{3} x^{2} + 8 x - 1, y_{2} = 6 x + 2$ ，当 $x$ 取何值时 $y_{1} = y_{2}$

查看试题解析
20. 已知当x=2时，二次三项式 $x^{2} - 2 m x + 8$ 的值等于4，那么当x为何值时，这个二次三项式的值是9？

查看试题解析

初中数学北师大版九年级上学期 第二章 2.2 配方法求解一元二次方程