高中数学人教A版(2019) 选修一 第一章 空间向量与立体几何
试卷更新日期:2021-07-24 类型:单元试卷
一、单选题
-
1. 已知O,A,B,C为空间不共面的四点,且向量 = ,向量 ,则不能与 构成空间的一个基底的是( )A、 B、 C、 D、 或2. 对于空间任意一点O和不共线的三点A,B,C,有如下关系: ,则( )A、四点O,A,B,C必共面 B、四点P,A,B,C必共面 C、四点O,P,B,C必共面 D、五点O,P,A,B,C必共面3. 在三棱锥 中, 是 的中点,且 ,则 ( )A、 B、 C、 D、4. 已知向量 =(1,5,﹣2), =(3,1,2), =(x,﹣3,6).若DE∥平面ABC,则x的值是( )A、5 B、3 C、2 D、﹣15. 已知且则x=( )
A、10 B、 C、3 D、6. 如图,四边形 , , ,现将 沿 折起,当二面角 的大小在 时,直线 和 所成角为 ,则 的最大值为( )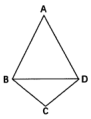 A、
A、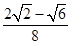 B、
B、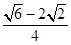 C、
C、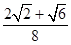 D、
D、 7. 在正三棱柱 中,D是AC的中点,AB1⊥BC1 , 则平面DBC1与平面CBC1所成的角为( )
7. 在正三棱柱 中,D是AC的中点,AB1⊥BC1 , 则平面DBC1与平面CBC1所成的角为( )
A、30° B、45° C、60° D、90°8. 已知正三棱柱 的侧棱长与底面边长相等,则AB1与侧面ACC1A1所成角的正弦值等于( )
A、 B、 C、 D、二、多选题
-
9. 如图,在长方体 中, , , ,以直线 , , 分别为 轴、 轴、 轴建立空间直角坐标系,则( )
 A、点 的坐标为 B、点 关于点 对称的点为 C、点 关于直线 对称的点为 D、点 关于平面 对称的点为10. 空间直角坐标系中,下列说法正确的是( )A、点 关于坐标平面 的对称点的坐标为 B、点 在平面 面上 C、 表示一个与坐标平面 平行的平面 D、 表示一条直线11. 已知向量 ,则与 共线的单位向量 ( )A、 B、 C、 D、12. 设动点 在正方体 的对角线 上,记 当 为钝角时,则实数可能的取值是( )A、 B、 C、 D、1
A、点 的坐标为 B、点 关于点 对称的点为 C、点 关于直线 对称的点为 D、点 关于平面 对称的点为10. 空间直角坐标系中,下列说法正确的是( )A、点 关于坐标平面 的对称点的坐标为 B、点 在平面 面上 C、 表示一个与坐标平面 平行的平面 D、 表示一条直线11. 已知向量 ,则与 共线的单位向量 ( )A、 B、 C、 D、12. 设动点 在正方体 的对角线 上,记 当 为钝角时,则实数可能的取值是( )A、 B、 C、 D、1三、填空题
-
13. 在空间直角坐标系 中,点 关于 轴的对称点坐标是.14. 如图,四棱柱 的底面 是正方形, 为底面中心, 平面 , .平面 的法向量 .
 15. 已知 , ,且 ,则 .16. 已知A(1,0,0),B(0,1,0),C(0,0,1),则平面ABC的一个单位法向量是 .
15. 已知 , ,且 ,则 .16. 已知A(1,0,0),B(0,1,0),C(0,0,1),则平面ABC的一个单位法向量是 .四、解答题
-
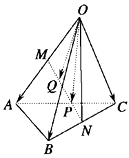
17. 如图所示,N,N分别是四面体OABC的棱OA,BC的中点,P,Q是MN的三等分点,用向量 , , 表示 和 .
 18. 已知
18. 已知
(1)、若(k+)∥(−3) ,求实数 k 的值;
(2)、若 ,求实数 的值.
19. 如图,在四棱锥P-ABCD中,PC⊥底面ABCD , 底面ABCD是直角梯形,AB⊥AD , AB∥CD , AB=2AD=2CD=2,E是PB的中点. (1)、求证:平面EAC⊥平面PBC;(2)、若二面角P-AC-E的余弦值为 ,求直线PA与平面EAC所成角的正弦值.20. 如图,已知四棱锥 的底面为等腰梯形,AB∥CD,AC⊥BD,垂足为H,PH是四棱锥的高,E为AD的中点.
(1)、求证:平面EAC⊥平面PBC;(2)、若二面角P-AC-E的余弦值为 ,求直线PA与平面EAC所成角的正弦值.20. 如图,已知四棱锥 的底面为等腰梯形,AB∥CD,AC⊥BD,垂足为H,PH是四棱锥的高,E为AD的中点. (1)、证明:PE⊥BC;(2)、若∠APB=∠ADB=60°,求直线PA与平面PEH所成角的正弦值.
(1)、证明:PE⊥BC;(2)、若∠APB=∠ADB=60°,求直线PA与平面PEH所成角的正弦值.
