河南省漯河市召陵区2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-07-23 类型：期末考试

进入出卷网下载

一、单选题

1. 若 $a^{2} = 9$ ， $\sqrt[3]{b} = - 2$ ，则 $a + b =$ （）

A、-5 B、-11 C、-5或-11 D、-5或11

查看试题解析
2. 袁隆平“超级杂交稻高产攻关科研基地”为了测算一块600亩试验田里新培育的杂交水稻的产量，随机对其中的10亩杂交水稻的产量进行了检测，在这个问题中，数字10是（）

A、个体 B、总体 C、样本容量 D、总体的样本

查看试题解析
3. 在平面直角坐标系中，将点A(m－1，n＋2)先向右平移3个单位，再向上平移2个单位，得到点A′．若点A′位于第二象限，则m、n的取值范围分别是（）

A、m＜0，n＞0 B、m＜0，n＜－2 C、m＜－2，n＞－4 D、m＜1，n＞－2

查看试题解析
4. 若 $a > b$ ，则下列不等式正确的是（）

A、 $3 a < 3 b$ B、 $m a > m b$ C、 $- a - 1 > - b - 1$ D、 $\frac{a}{2} + 1 > \frac{b}{2} + 1$

查看试题解析
5. 下列调查方式选取合适的是（）

A、为了解一批防疫物资的质量情况，选择普查 B、为了解全市居民日平均用水量，选择普查 C、为了解全市中小学生对新冠病毒传播途径的知晓率，选择抽样调查 D、为了解运载火箭的零部件的质量情况，选择抽样调查

查看试题解析
6. 如图，直线 $l_{1} // l_{2}$ ，且分别与直线 $l$ 交于 $C$ 、 $D$ 两点，把一块含 $30 °$ 角的三角尺按如图所示的位置摆放，若 $∠ 1 = 52 °$ ，则 $∠ 2$ 的度数是（）

A、 $97 °$ B、 $98 °$ C、 $100 °$ D、 $108 °$

查看试题解析
7. 若二元一次方程组 ${\begin{array}{l} x + y = 3, \\ 3 x - 5 y = 4 \end{array}$ 的解为 ${\begin{array}{l} x = a, \\ y = b, \end{array}$ 则a-b的值为（）

A、1 B、3 C、 $- \frac{1}{4}$ D、 $\frac{7}{4}$

查看试题解析
8. 若不等式组 ${\begin{matrix} x - 2 < 3 x - 6 \\ x < m \end{matrix}$ 无解，则m的取值范围是（）

A、m＞2 B、m＜2 C、m≥2 D、m≤2

查看试题解析
9. 二元一次方程3x﹣2y=1的不超过10的正整数解共有（）组.

A、1 B、2 C、3 D、4

查看试题解析
10. 某市居民用电的电价实行阶梯收费，收费标准如下表：

一户居民每月用电量x(度)

电费价格(元/度)

$0 < x ⩽ 200$

0.48

$200 < x ⩽ 400$

0.53

$x > 400$

0.78

七月份是用电高峰期，李叔计划七月份电费支出不超过200元，则李叔家七月份最多可用电的度数是（）.

A、100 B、400 C、396 D、397

查看试题解析

二、填空题

11. 请你写出一个大于2小于3的无理数是．

查看试题解析
12. $\sqrt[3]{64}$ 的平方根为

查看试题解析
13. 如图，点E在AC的延长线上，对于给出的四个条件：（1）∠3=∠4；（2）∠1=∠2；（3）∠A=∠DCE；（4）∠D+∠ABD=180°.能判断AB∥CD的有个.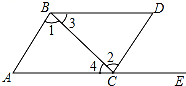

查看试题解析
14. 如果关于x的不等式组 ${\begin{array}{l} 3 x-a \geq 0 ， \\ 2 x-b \leq 0 \end{array}$ 的整数解仅有1，2，那么适合这个不等式组的整数a，b组成的有序数对(a，b)共有个.

查看试题解析

三、解答题

15. 如图，将 $△ A B C$ 沿直线 $A B$ 向右平移后到达 $△ B D E$ 的位置，若 $∠ C A B = 50 °$ ， $∠ B D E = 100 °$ ，则 $∠ C B E$ 的度数为.

查看试题解析
16. 解不等式组： ${\begin{array}{l} 2 (x + 1) \geq x ① \\ \frac{x + 1}{2} > x - 1 ② \end{array}$
请结合题意填空，完成本题的解题.

(1)、解不等式①，得；

(2)、解不等式②，得；

(3)、把不等式①和②的解集在数轴上表示出来；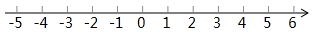

(4)、原不等式组的解集为.

查看试题解析
17. 已知实数a，b，c满足 $b = \sqrt{- {(a - 3)}^{2}} + 4$ ，c的平方根等于它本身.求 $a + \sqrt{b - c}$ 的值.

查看试题解析
18. 为了创设全新的校园文化氛围，让学生在丰富多彩的书海中扩大知识源，某校准备开展“与经典为友、与名著作伴”的课外阅读活动，活动前对本校学生进行了“你最喜欢的图书类型（只写一项）”的随机抽样调查，相关数据统计如下：

(1)、该校对名学生进行了抽样调查.

(2)、请将图1和图2补充完整；并求出扇形统计图中小说所对应的圆心角度数.

(3)、已知该校共有学生800人，利用样本数据估计全校学生中最喜欢漫画人数约为多少人？

查看试题解析
19. 如图，已知∠1＋∠2＝180°，∠DEF ＝∠A ，∠BED ＝60°，求∠ACB的度数.

查看试题解析
20. 已知方程组 ${\begin{array}{l} a x + 5 y = 15 ① \\ 4 x + b y = - 2 ② \end{array}$ ，由于甲看错了方程①中的 $a$ ，得到方程组的解为 ${\begin{array}{l} x = - 3 \\ y = - 1 \end{array}$ ，乙看错了方程②中的 $b$ ，得到方程组的解为 ${\begin{array}{l} x = 5 \\ y = 2 \end{array}$ ，试求出 $\frac{a^{2021}}{b}$ 的值.

查看试题解析
21. 受“新冠肺炎”疫情影响，市场上医用口罩出现热销.某药店准备购进一批医用口罩已知 $1$ 个 $A$ 型口罩和2个 $B$ 型口罩共需18元：2个 $A$ 型口罩和 $1$ 个 $B$ 型口罩共需12元

(1)、求一个 $A$ 型口罩和一个 $B$ 型口罩的进价各是多少元？

(2)、药店准备购进这两种型号的口罩共100个，其中 $A$ 型口罩数量不少于64个，且不多于 $B$ 型口罩的2倍，有哪几种购买方案，哪种方案购进总费用最少？

查看试题解析
22. 某园林的门票每张10元，一次使用，考虑到人们的不同需求，也为了吸引更多的游客，该园林除保留原来的售票方法外，还推出了一种“购买个人年票”的售票方法(个人年票从购买日起，可供持票者使用一年).年票分A、B、C三类：A类年票每张120元，持票者进入园林时，无需再用门票；B类年票每张60元，持票者进入该园林时，需再购买门票，每次2元；C类年票每张40元，持票者进入该园林时，需再购买门票，每次3元.

(1)、如果只选择一种购买门票的方式，并且计划在一年中用不多于80元花在该园林的门票上，试通过计算，找出可进入该园林次数最多的购票方式，

(2)、一年中进入该园林至少超过次时，购买A类年票最合算.

查看试题解析
23. 如图1，在平面直角坐标系中，点 $A$ ， $B$ 的坐标分别为 $(- 1 ， 0)$ ， $(3 ， 0)$ ，现同时将点 $A$ ， $B$ 分别向上平移2个单位长度，再向右平移1个单位长度，得到 $A$ ， $B$ 的对应点 $C$ ， $D$ ，连接 $A C$ ， $B D$ ， $C D$ .

(1)、写出点 $C$ ， $D$ 的坐标并求出四边形 $A B D C$ 的面积.

(2)、在 $x$ 轴上是否存在一点 $F$ ，使得三角形 $D F C$ 的面积是三角形 $D F B$ 面积的2倍，若存在，请求出点 $F$ 的坐标；若不存在，请说明理由.

(3)、如图2，点 $P$ 是直线 $B D$ 上一个动点，连接 $P C$ ， $P O$ ，当点 $P$ 在直线 $B D$ 上运动时，请直接写出 $∠ O P C$ 与 $∠ P C D$ ， $∠ P O B$ 的数量关系.

查看试题解析

一户居民每月用电量x(度)	电费价格(元/度)
$0 < x ⩽ 200$	0.48
$200 < x ⩽ 400$	0.53
$x > 400$	0.78