重庆市江津区2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期：2021-07-23 类型：期末考试
一、单选题
-
1. 下列各数是最简二次根式的是（ ）A、 B、 C、 D、2. 已知直角三角形的两条直角边的长分别是1， ，则斜边长为（ ）A、1 B、 C、2 D、33. 直线y=2x向下平移2个单位长度得到的直线是（ ）A、y=2（x+2） B、y=2（x﹣2） C、y=2x﹣2 D、y=2x+24. 下列计算正确的是（ ）A、3+ ＝3 B、 ﹣ ＝ C、 × ＝ D、 ÷2＝5. 已知△ABC的三边分别是a、b、c，下列条件中不能判断△ABC为直角三角形的是（ ）A、a2+b2=c2 B、∠A+∠B=90° C、a=3，b=4，c=5 D、∠A：∠B：∠C=3：4：56. 在今年的中招体育考试中，我校甲、乙、丙、丁四个班级的平均分完全一样，方差分别为：S甲2=8.5，S乙2=21.7，S丙2=15，S丁2=17.2，则四个班体考成绩最稳定的是（ ）A、甲班 B、乙班 C、丙班 D、丁班7. 下列说法正确的是（ ）A、一组对边平行另一组对边相等的四边形是平行四边形 B、对角线互相垂直平分的四边形是菱形 C、对角线相等的四边形是矩形 D、对角线互相垂直且相等的四边形是正方形8. 如图，在平行四边形ABCD，O是AC、BD的交点，过点O与AC垂直的直线交边AD于点E，若△CDE的周长为11cm，则平行四边形ABCD的周长为（ ）
A、20cm B、22cm C、24cm D、26cm9. 下列图形都是由同样大小的小圆圈按一定规律所组成的，其中第①个图形中一共有6个小圆圈，第②个图形中一共有9个小圆圈，第③个图形中一共有12个小圆圈，⋯，按此规律排列，则第⑧个图形中小圆圈的个数为（ ）
A、24 B、27 C、30 D、3310. 如图，平行四边形ABCD的对角线AC与BD相交于点O.CE⊥AD于点E，AB＝2 ，AC＝4，BD＝8，则CE＝（ ）
A、 B、 C、 D、11. 若关于x的一次函数y＝（k﹣2）x+3，y随x的增大而减小，且关于x的不等式组 无解，则符合条件的所有整数k的值之和是（ ）A、﹣3 B、﹣2 C、﹣1 D、012. 一条公路旁依次有A，B，C三个村庄，甲、乙两人骑自行车分别从A村、B村同时出发前往C村，甲、乙之间的距离s（km）与骑行时间t（h）之间的函数关系如图所示，下列结论：①A，B两村相距10km；②甲出发2h后到达C村；③甲每小时比乙多骑行8km；④相遇后，乙又骑行了30min或55min时两人相距4km.其中正确的是（ ）
A、①③④ B、①②③ C、①②④ D、①②③④二、填空题
-
13. 函数 中，自变量x的取值范围是 ．14. 重庆农村医疗保险已经全面实施.某县七个村中享受了住院医疗费用报销的人数分别为：20，24，27，28，31，34，38，则这组数据的中位数是.15. 已知一次函数y＝kx+b（k＞0）的函数图象过点（3，0），则关于x的不等式3kx﹣b≤0的解集为.16. 如图，在平行四边形ABCD中，∠D＝100°，∠DAB的平分线AE交CD于点E.连接BE，若AE＝AB，则∠AEB的度数为.
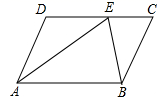17. 如图，在菱形ABCD中，对角线AC、BD相交于点O，AC＝16，BD＝12，E是边AD上一点，直线OE交BC于点F，将菱形沿直线EF折叠，使点B的对应点为B'，点A的对应点为A′，若AE＝4，则 的长等于.
18. 如图，在Rt△ABC中，∠C＝90°，∠A＝30°，BC＝8，若点P是边AB上的一个动点，以每秒3个单位的速度按照从A→B→A运动，同时点Q从B→C以每秒1个单位的速度运动，当一个动点到达终点时，另一个动点也随之停止运动.在运动过程中，设运动时间为t，若△BPQ为直角三角形，则t的值是.
三、解答题
-
19. 计算：(1)、 ；(2)、（ ﹣1）2﹣（ +1）（ ﹣1）.20. 如图，AC=8，分别以A、C为圆心，以长度5为半径作弧，两条弧分别相交于点B和D。依次连接A、B、C、D，连接BD交AC于点O。
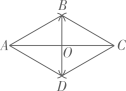(1)、判断四边形ABCD的形状并说明理由；(2)、求BD的长。21. 某校为弘扬女排精神，组织八年级学生进行排球知识竞赛，现从男、女生中各随机抽取10名学生的竞赛成绩（百分制）进行整理、描述和分析（成绩用x表示），下面给出了部分信息：抽取的10名男生竞赛成绩是：89 96 90 96 98 100 92 83 43 93
抽取的10名女生竞赛成绩在85≤s≤100分数段的为：95 95 87 88 100 95 92
抽取的男、女生竞赛成绩统计表
性别
平均数
中位数
众数
男生
88
a
c
女生
88
b
95
根据以上信息，解答下列问题：
(1)、填空：a＝ ， b＝ ， c＝；(2)、观察上面数据后，小李认为男生对排球知识了解的更多，小张认为女生对排球知识了解的更多.你同意 ▲ 的看法，并说明理由（从一个角度说明推断的合理性）；(3)、若八年级有男、女生各200名，估计八年级学生的竞赛成绩在85分及以上的学生有多少人？22. 小敏根据学习函数的经验，对函数y＝|x﹣2|+1图象与性质进行了探究，下面是小敏的探充过程，请补充完整.(1)、函数y＝|x﹣2|+1的自变量x可以取 ；(2)、列表，写出y与x的几组对应值：x
…
﹣3
﹣2
﹣1
0
1
2
3
…
y
…
6
5
4
3
2
1
2
…
若A（9，8），B（m，8）为该函数图象上不同的两点，则m＝；
(3)、在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点，并根据描出的点，画出该函数的图象，根据图象可得：①该函数的最小值为 ▲ ；
②结合你所画的函数图象，直接写出关于x的方程|x﹣2|+1＝n有两个解时，n的取值范围： ▲ .
23. 喜欢探索数学知识的小明遇到一个新的定义：对于三个互不相等的正整数，若其中任意两个数乘积的算术平方根都是整数，则称这三个数为“老根数”，其结果中最小的整数称为“最小算术平方根”，最大的整数称为“最大算术平方根”.例如：1，4，9这三个数， ＝2， ＝3， ＝6，其结果分别为2，3，6都是整数，所以1，4，9这三个数称为“老根数”，其中“最小算术平方根”是2，“最大算术平方根”是6.(1)、请证明：2，8，50这三个数是“老根数”，并求出任意两个数乘积的最小算术平方根与最大算术平方根；(2)、已知16，a，36这三个数是“老根数”，且任意两个数乘积的算术平方根中，最大算术平方根是最小算术平方根的2倍，求a的值.24. 某超市欲购进A，B两种品牌的T恤共300件，已知两种T恤的进价如表所示.设购进A种T恤x件，且所购进的两种T恤全部卖出，获得的总利润为w元.品牌
进价（无/件）
售价（元/件）
A
60
85
B
50
70
(1)、求w关于x的函数关系式；(2)、如果购进两种T恤的总费用不超过16500元，那么超市如何进货才能获得最大利润？并求出最大利润.（提示：利润＝售价﹣进价）25. 如图，在正方形ABCD中，E是CD边上的一动点（不与点C，D重合），连接AE，将△ADE沿着AE翻折得到△AEF，延长EF交BC于点G，连接AG，过点E作EH⊥AE交AG的延长线于点H，连接CH.
(1)、求∠EAH的度数；(2)、求证：CH＝ DE.26. 如图，平面直角坐标系中，已知点C的坐标为（ ，﹣2），直线AB与x轴、y轴分别交于点A、点B，且点B的坐标为（0，3），∠BAO＝30°.
(1)、求直线AB的解析式；(2)、若点D是y轴上一动点，点E（ ，m）在直线AB上，当CD+DE取得最小值时，求出D、E两点的坐标；(3)、在（2）的条件下，是否存在点P使得以P、C、D、E为顶点的四边形是平行四边形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由.