重庆市长寿区2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-07-23 类型:期末考试
一、单选题
-
1. 式子 有意义,则x的取值范围是( )
A、x>1 B、x<1 C、x≥1 D、x≤12. 计算 的值为( )A、2 B、3 C、 D、3. 下列各组数中,以它们为边长的线段不能构成直角三角形的是( )A、1, , B、3,4,5 C、5,12,13 D、2,3,44. 已知一个平行四边形两邻边的长分别为10和6,那么它的周长为( )A、16 B、60 C、32 D、305. 在今年的中招体育考试中,某校甲、乙、丙、丁四个班的平均分完全一样,方差分别为: , , , ,则四个班学生体育考试成绩最均衡的是( )A、甲班 B、乙班 C、丙班 D、丁班6. 估计 的运算结果在哪两个整数之间( )A、1和2 B、2和3 C、3和4 D、4和57. 五个绿化小组一天植树的棵树如下:10、10、12、 、8.已知这组数据的众数与平均数相同,那么这组数据的平均数是( )A、12 B、10 C、8 D、98. 下列各组数不能作为直角三角形三边长的是( )A、 , , B、3,4,5 C、5,12,13 D、1,2,9. 如图,正比例函数 ( ≠0)和一次函数 ( ≠0)的图象相交于点A(1,1),则不等式 的解集是( ) A、 B、 C、 <1 D、 >110. 已知菱形的周长为40 ,两条对角线的长度比为3:4,那么两条对角线的长分别为( )A、6 ,8 B、3 ,4 C、12 ,16 D、24 ,3211.
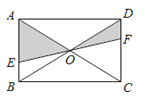
A、 B、 C、 <1 D、 >110. 已知菱形的周长为40 ,两条对角线的长度比为3:4,那么两条对角线的长分别为( )A、6 ,8 B、3 ,4 C、12 ,16 D、24 ,3211.如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD的面积的( )
 A、 B、 C、 D、12. 如果关于 的一次函数 的图象不经过第二象限,且关于 的分式方程 有整数解,那么所有满足条件的整数 的值的和是( )A、8 B、7 C、5 D、3
A、 B、 C、 D、12. 如果关于 的一次函数 的图象不经过第二象限,且关于 的分式方程 有整数解,那么所有满足条件的整数 的值的和是( )A、8 B、7 C、5 D、3二、填空题
-
13. 若 ,则m-n的值为 .14. 将函数 的图象向下平移2个单位后得到的图象的函数解析式为.15. 如图,在菱形ABCD中对角线AC、BD相交于点O,若AB=3,BD=4,则菱形ABCD的面积为.
 16. 小芳测得连续五天日最低气温并整理后得出下表:
16. 小芳测得连续五天日最低气温并整理后得出下表:日期
一
二
三
四
五
平均气温
方差
最低气温
1
3
2
5
4
3

由于不小心被墨迹污染了一个数据,这个数据(方差)是.
17. 甲、乙两车分别从A,B两地同时相向匀速行驶. 当乙车到达 地后,继续保持原速向远离 的方向行驶,而甲车到达 地后立即掉头,并保持原速与乙车同向行驶,经过一段时间后两车同时到达 地. 设两车行驶的时间为 (小时),两车之间的距离为 (千米), 与 之间的函数关系如图所示,当甲车到达 地时,乙车距离 地千米.
 18. 在正方形ABCD中,对角线AC、BD交于点O,点E在DO上,DE=2EO,连接AE,将△ADE沿AD翻折,得△ADE′,点F是AE的中点,连接 .若DE= ,则△AFE′的面积是.
18. 在正方形ABCD中,对角线AC、BD交于点O,点E在DO上,DE=2EO,连接AE,将△ADE沿AD翻折,得△ADE′,点F是AE的中点,连接 .若DE= ,则△AFE′的面积是.
三、解答题
-
19. 计算: .20. 如图:在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
 21. 如图,折叠矩形ABCD的顶点D所在角,使点D落在BC边上的点F处,折痕为AE.
21. 如图,折叠矩形ABCD的顶点D所在角,使点D落在BC边上的点F处,折痕为AE.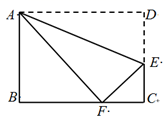 (1)、若∠DAE=25°,求∠EFC 的大小;(2)、若AB=8,BC=10,求EF的长.22. 某教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行统计调查,并绘制了统计表及统计图,如图所示:
(1)、若∠DAE=25°,求∠EFC 的大小;(2)、若AB=8,BC=10,求EF的长.22. 某教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行统计调查,并绘制了统计表及统计图,如图所示: (1)、这50名学生每人一周内的零花钱数额的平均数是元;众数是元;中位数是元,学生每人一周内的零花钱数额的极差为.(2)、据统计该校的1800人中,每人每周的零花钱有 在学校超市消费,试估计该校学生每周在学校超市消费的零花钱总金额为多少元?23. 为了创建文明城市,绿化城市环境,我区计划在某公园种植榆树.现有甲、乙两家苗圃有质量相同的榆树苗可供选择,其具体销售方案如下表:
(1)、这50名学生每人一周内的零花钱数额的平均数是元;众数是元;中位数是元,学生每人一周内的零花钱数额的极差为.(2)、据统计该校的1800人中,每人每周的零花钱有 在学校超市消费,试估计该校学生每周在学校超市消费的零花钱总金额为多少元?23. 为了创建文明城市,绿化城市环境,我区计划在某公园种植榆树.现有甲、乙两家苗圃有质量相同的榆树苗可供选择,其具体销售方案如下表:甲苗圃
购树苗数量
销售单价
不超过1000棵时
4元/棵
超过1000棵的部分
3.8元/棵
乙苗圃
购树苗数量
销售单价
不超过2000棵时
4元/棵
超过2000棵的部分
3.6元/棵
设购买榆树苗 棵,到甲、乙两家苗圃购买榆树苗所需费用分别为 (元)、 (元).
(1)、直接写出 , 与 之间的函数关系式;(2)、如果购买榆树苗超过2000棵,应该选择到哪家苗圃购买合算,为什么?24. 如图,四边形ABCD是正方形,点M在边BC上(不与端点B、C重合),点N在对角线AC上,且MN⊥AC,连接AM,点G是AM的中点,连接NG、DN. (1)、若AB=10,BM=2 ,求NG的长;(2)、求证:DN= NG.25. 如图1,一次函数 的图象与 轴、 轴分别交于点 、点 ,与正比例函数 的图象交于点 ,将点 向右平移1个单位,再向下平移6个单位得到点 .
(1)、若AB=10,BM=2 ,求NG的长;(2)、求证:DN= NG.25. 如图1,一次函数 的图象与 轴、 轴分别交于点 、点 ,与正比例函数 的图象交于点 ,将点 向右平移1个单位,再向下平移6个单位得到点 . (1)、求 的周长和点 的坐标;(2)、如图2,点 是 轴上一动点,当 最小时,求点 的坐标;(3)、若点 是 轴上一动点,当 为等腰三角形时,直接写出点 的坐标.26. 如图,在以O为原点的平面直角坐标系中,四边形OBNM是矩形,点B的坐标为(2,0),点A的坐标为(0,2),线段MN(MN∥OB)交AB于点P,连接OP,作直线PC⊥PO,交直线BN于点C.
(1)、求 的周长和点 的坐标;(2)、如图2,点 是 轴上一动点,当 最小时,求点 的坐标;(3)、若点 是 轴上一动点,当 为等腰三角形时,直接写出点 的坐标.26. 如图,在以O为原点的平面直角坐标系中,四边形OBNM是矩形,点B的坐标为(2,0),点A的坐标为(0,2),线段MN(MN∥OB)交AB于点P,连接OP,作直线PC⊥PO,交直线BN于点C. (1)、当点C在第一象限时,求证:△OPM≌△PCN;(2)、当点C在第一象限时,设AP的长为 ,△OPB的面积为 ,求出 与 之间的函数关系式(不写自变量的取值范围);(3)、当点P在线段AB上移动时,△PBC是否可能成为等腰三角形?如果可能,请直接写出所有能使△PBC成为等腰三角形的点P的坐标;如果不可能,请说明理由.
(1)、当点C在第一象限时,求证:△OPM≌△PCN;(2)、当点C在第一象限时,设AP的长为 ,△OPB的面积为 ,求出 与 之间的函数关系式(不写自变量的取值范围);(3)、当点P在线段AB上移动时,△PBC是否可能成为等腰三角形?如果可能,请直接写出所有能使△PBC成为等腰三角形的点P的坐标;如果不可能,请说明理由.