重庆市万州区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-07-23 类型：期末考试

进入出卷网下载

一、单选题

1. 在 $\frac{1}{x}$ 、 $\frac{1}{2}$ 、 $\frac{3 x y}{π}$ 、 $\frac{x^{2} - 2 y^{3}}{x + 3 y}$ 、 $\frac{x^{2} + 1}{5}$ 、 $\frac{m - n}{7 a b}$ 中，分式的个数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 下面4个汽车标识图案不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列变形正确的是（）

A、 $\frac{a}{b}$ ＝ $\frac{a + 2}{b + 2}$ B、 $\frac{0.2 a + b}{0.1 b} = \frac{2 a + b}{b}$ C、 $\frac{a}{b}$ -1= $\frac{a - 1}{b}$ D、 $\frac{a}{b}$ = $\frac{a (m^{2} + 1)}{b (m^{2} + 1)}$

查看试题解析
4. 已知点P（m﹣1，4）与点Q（2，n﹣2）关于x轴对称，则mⁿ的值为（）

A、9 B、﹣9 C、﹣ $\frac{1}{9}$ D、 $\frac{1}{9}$

查看试题解析
5. 下列四个命题中，真命题有）
①两条直线被第三条直线所截，内错角相等.②如果∠1和∠2是对顶角，那么∠1＝∠2.③三角形的一个外角大于任何一个内角.④如果x²＞0，那么x＞0.

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 根据如图所示的程序计算函数y的值，若输入的x值是－3和4时，输出的y值相等，则m等于（）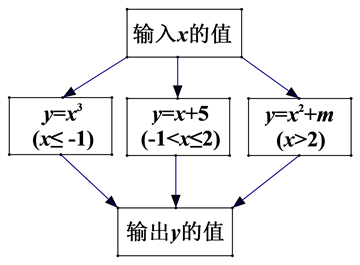

A、－17 B、－25 C、25 D、－43

查看试题解析
7. 如图，在△MPN中，H是高MQ和NR的交点，且MQ=NQ，已知PQ＝5，NQ＝9，则MH的长为（）

A、3 B、4 C、5 D、6

查看试题解析
8. 若9x=5y，则 $\frac{x}{y}$ =（）

A、 $\frac{9}{5}$ B、 $\frac{5}{9}$ C、 $\frac{9}{4}$ D、 $\frac{4}{9}$

查看试题解析
9. 如图，菱形ABCD的对角线AC、BD相交于点O，AC＝10，BD=4，EF为过点O的一条直线，则图中阴影部分的面积为（）

A、5 B、6 C、8 D、12

查看试题解析
10. 如图，函数 $y = \frac{k}{x}$ （k＞0）的图象经过矩形OABC的边BC的中点E，若四边形ODBC的面积为6，则k的值为（）

A、2 B、3 C、4 D、6

查看试题解析
11. 关于 $x$ 的分式方程 $\frac{x}{x - 2} - \frac{a + 8}{2 - x} = - 3$ 的解为非负整数，且一次函数 $y = (a - 6) x + 14 + a$ 的图象不经过第三象限，则满足条件的所有整数 $a$ 的和为（）

A、-22 B、-12 C、-14 D、-8

查看试题解析
12. 如图，正方形ABDC中，AB＝6，DE＝2，将△ADE沿AE折叠至△AFE，连AG、CF，下列结论：①△ABG≌△AFG；②BG＝CG；③AG $//$ CF；④S_△FCG＝3，其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 计算： $3^{- 2} + {(π - 3.14)}^{0} =$ .

查看试题解析
14. 数据6，5，x，4，7的平均数是5，那么这组数据的方差为；

查看试题解析
15. 如图，直线 $y = k x + b$ （ $k < 0$ ， $k$ ， $b$ 为常数）经过 $A (3 ， 1)$ ，则不等式 $k x + b < 1$ 的解为.

查看试题解析
16. 菱形ABCD中，∠B＝60°，AB＝5，以AC为边长作正方形ACFE，则点D到EF的距离为.

查看试题解析
17. 甲、乙两人同时从 $A$ 、 $B$ 两地出发相向而行，甲先步行到达 $B$ 地后原地休息，甲、乙两人的距离 $y (k m)$ 与乙步行的时间 $x (h)$ 之间的函数关系的图象如图，则步行全程甲比乙少用小时.

查看试题解析
18. △ABC中，AB=AC=12厘米，∠B=∠C，BC=8厘米，点D为AB的中点．如果点P在线段BC上以2厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．若点Q的运动速度为v厘米/秒，则当△BPD与△CQP全等时，v的值为．

查看试题解析

三、解答题

19.

(1)、计算 $\frac{4 x}{3 y} \cdot \frac{y}{2 x^{4}} \div {(\frac{1}{x})}^{2}$ ；

(2)、计算（ $\frac{a}{a - b} - \frac{2 b}{a - b}$ ） $\div \frac{a - 2 b}{a}$ ；

(3)、解方程： $\frac{1}{x - 3} + \frac{x}{3 - x} = 1$ ；

(4)、解方程： $\frac{2}{3} + \frac{x}{3 x - 1} = \frac{1}{9 x - 3}$ .

查看试题解析
20. 已知，如图，在▱ABCD中，BF平分∠ABC交AD于点F，AE⊥BF于点O，交BC于点E，连接EF.

(1)、求证：四边形ABEF是菱形：

(2)、若菱形ABEF的周长为16，∠BEF＝120°，求AE的大小.

查看试题解析

21. 某学校七年级共有1500名学生，为了解学生的身体素质情况，年级从甲、乙两个班各抽取20名学生进行体能测试，这些学生的测试成绩如下：

甲班：79，87，75，76，77，71，76，76，79，71，75，87，63，78

乙班：94，73，89，72，82，84，80，81，82，82，74，83，81，41

成绩	x＜60	60≤x＜70	70≤x＜80	80≤x＜90	90≤x≤100
甲班	0	1	12	6	1
乙班	1	0	6	11	2

（注：若80≤x≤100，体能优秀；若70≤x＜80，体能良好；若60≤x＜70，体能合格；若x＜60，体能不合格）

两组样本数据的平均数、中位数、众数如表所示：

班级	平均数	中位数	众数	优秀率
甲	79	a	76	c
乙	79	81.5	b	60%

回答以下问题：

(1)、a＝， b＝， c＝；

(2)、通过以上数据的分析，你认为哪个班的学生的体能水平更高，并说明理由（写出一条即可）.

(3)、估计一下该校七年级体能优秀的人数有多少人？

查看试题解析

22. 学习了“分式的加减法”的相关知识后，小亮同学画出了下图：

(1)、请问他画的图中①为， ②为.

(2)、结合上面的流程图，请列举出一组分式的加减法并且进行计算，同时满足如下条件：
①两个异分母分式相加；

②分母都是单项式；

③所含的字母不得多于2个.

列举并计算：

查看试题解析
23. 某经销商3月份用18000元购进一批T恤衫售完后，4月份用39000元购进一批相同的T恤衫，数量是3月份的2倍，但每件进价涨了10元，

(1)、4月份进了这批T恤衫多少件？

(2)、4月份，经销商将这批T恤衫平均分给甲、乙两家分店销售，每件标价180元.甲店按标价卖出a件以后；乙店同样按标价卖出a件，然后将b件按标价九折售出，结果利润与甲店相同.
①用含a的代数式表示b.

②已知乙店按标价售出的数量不超过九折售出的数量，请你求出乙店利润的最大值.

查看试题解析

24. 某数学兴趣小组的同学在研究函数

y = \frac{1}{| x + 1 |} + 1

的图象时，先对函数

y = \frac{1}{| x |}

的图象进行了如下探索.

(1)、①列表：列出

y

与

x

的几组对应值如下：

$x$	···	-3	-2	-1	$- \frac{1}{2}$	$- \frac{1}{3}$	$\frac{1}{3}$	$\frac{1}{2}$	1	2	3	···
$y$	···	$\frac{1}{3}$	$\frac{1}{2}$	1	2	3	3	2	1	$\frac{1}{2}$	$\frac{1}{3}$	···

②描点：根据表中数据描点如图所示；

③连线：请在图中画出函数 $y = \frac{1}{| x |}$ 的图象；

④观察图象，写出两条关于该函数的性质.

(2)、根据以上探究结果，完成下列问题：

①函数 $y = \frac{1}{| x + 1 |} + 1$ 中，自变量 $x$ 的取值范围为 ▲ ；

②函数 $y = \frac{1}{| x + 1 |} + 1$ 的图象可由函数 $y = \frac{1}{| x |}$ 的图象经过怎样的变换得到?

③写出两条关于函数 $y = \frac{1}{| x + 1 |} + 1$ 的性质；

④直接写出不等式 $\frac{1}{| x + 1 |} + 1 > 2$ 的解集.

查看试题解析

25. 当k值相同时，我们把正比例函数 $y = \frac{1}{k} x$ 和反比例函数 $y = \frac{k}{x}$ ，以函数y＝﹣ $\frac{1}{2}$ x和y＝﹣ $\frac{2}{x}$ ，下面是小亮的探究过程，请你将它补充完整.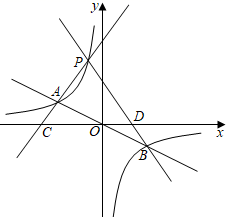

(1)、如图，在同一直角坐标系中画出这两个函数的图象，两个函数图象在第二、四象限分别交于点A，B，B的坐标分别是A ， B.

(2)、点P是函数y＝﹣ $\frac{2}{x}$ 在第二象限内的图象上的一个动点（不与点A重合），作直线PA，分别与x轴交于点C，D.设点P的横坐标为t.小亮通过分析得到：在点P运动的过程中，总有PC＝PD，
证明PC＝PD的过程如下（不完整）.

易知点P的坐标是（t，﹣ $\frac{2}{t}$ ）.

设直线AP的解析式为y＝ax+b.

将点A，P的坐标分别代入，得 ${\begin{matrix} - 2 a + b = 1 \\ t a + b = - \frac{2}{t} \end{matrix}$ ，解得 ${\begin{matrix} a = - \frac{1}{t} \\ b = \frac{2 - t}{t} \end{matrix}$

∴直线AP的解析式为y＝﹣ $\frac{1}{t}$ x﹣ $\frac{2 - t}{t}$ .

令y＝0，得x＝t﹣2，则点C的坐标为（t﹣2，0）.

同理可求得直线PB的解析式为y＝ $\frac{1}{t}$ x﹣ $\frac{t - 2}{t}$ .

…

请你补充剩余的证明过程.

(3)、当△PCD是等边三角形时，t＝.

(4)、随着点P的运动，△ABP的面积S与点P的横坐标t之间存在一定的函数关系，当t＞﹣2时，求S关于t的函数关系式.

查看试题解析
26. 勾股定理是数学史上非常重要的一个定理.早在2000多年以前，人们就开始对它进行研究，至今已有几百种证明方法.在欧几里得编的《原本》中证明勾股定理的方法如下，请同学们仔细阅读并解答相关问题：如图，分别以 $R t Δ A B C$ 的三边为边长，向外作正方形 $A B D E$ 、 $B C F G$ 、 $A C H I$ .

(1)、连接 $B I$ 、 $C E$ ，求证： $Δ A B I ≅ Δ A E C$

(2)、过点 $B$ 作 $A C$ 的垂线，交 $A C$ 于点 $M$ ，交 $I H$ 于点 $N$ .
①试说明四边形 $A M N I$ 与正方形 $A B D E$ 的面积相等；

②请直接写出图中与正方形 $B C F G$ 的面积相等的四边形.

(3)、由第（2）题可得：正方形 $A B D E$ 的面积 $+$ 正方形 $B C F G$ 的面积 $=$ 的面积，即在 $R t Δ A B C$ 中， $A B^{2} + B C^{2} =$ .

查看试题解析