浙江省宁波市镇海区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-07-23 类型：期末考试

进入出卷网下载

一、单选题

1. 下列垃圾分类图标中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列化简结果正确的是（）

A、 $\sqrt{2} \times \sqrt{3} = \sqrt{12}$ B、 $\sqrt{\frac{4}{3}} = \frac{2}{\sqrt{3}}$ C、 $\sqrt{36} = \pm 6$ D、 $3 \sqrt{3} - 2 \sqrt{3} = \sqrt{3}$

查看试题解析

3. 下表记录了四位射击运动员选拔比赛成绩的平均数和方差：

运动员	甲	乙	丙	丁
平均数（环）	9.1	9.2	9.1	9.2
方差（环 $^{2}$ ）	3.5	15.5	16.5	3.5

根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

4. 在 $▱ A B C D$ 中，若 $∠ A + ∠ C = 70 °$ ，则 $∠ B$ 的度数为（）

A、 $145^{°}$ B、 $115^{°}$ C、 $110^{°}$ D、 $150^{°}$

查看试题解析
5. 如图，点 $A 、 B$ 落在第二象限内双曲线 $y = \frac{k}{x} (k \neq 0)$ 上，过 $A 、 B$ 两点分别作 $x$ 轴的垂线段，垂足为 $C ， D$ ，连接 $O A 、 O B$ ，若 $S_{1} + S_{2} = 2$ 且 $S_{阴影} = 1$ ，则 $k$ 的值为（）

A、4 B、-4 C、2 D、-2

查看试题解析
6. 用反证法证明命题“在同一平面内，若 $a ⊥ b ， c ⊥ b$ ，则 $a / / c$ ”时，首先应假设（）

A、 $a / / b$ B、 $c / / b$ C、 $a$ 与 $c$ 相交 D、 $a$ 与 $b$ 相交

查看试题解析
7. 学校初二年级组织足球联赛，赛制为单循环制（每两个队之间比赛一场).共进行了 $28$ 场比赛，问初二年级有几个参赛班级？设初二年级有 $x$ 个班级参加比赛.根据题意列出方程正确的是（）

A、 $x^{2} = 28$ B、 $\frac{1}{2} x (x - 1) = 28$ C、 $\frac{1}{2} x^{2} = 28$ D、 $x (x - 1) = 28$

查看试题解析
8. 如图是二次函数 $y_{1} = a x^{2} + b x + c (a \neq 0)$ 和一次函数 $y_{2} = m x + n (m \neq 0)$ 的图象.则下列结论正确的是（）

A、若点 $M (- 2 ， d_{1}) ， N (\frac{1}{2} ， d_{2}) ， P (2 ， d_{3})$ 在二次函数图象上，则 $d_{1} < d_{2} < d_{3}$ B、当 $x < - \frac{1}{2}$ 或 $x > 3$ 时， $y_{1} > y_{2}$ C、 $2 a - b = 0$ D、当 $x = k^{2} + 2$ （ $k$ 为实数）时， $y_{1} \leq c$

查看试题解析
9. 如图1，图形 $A$ 、图形 $B$ 是含 $60^{°}$ 内角的全等的平行四边形纸片（非菱形)，先后按图2( $2 B$ )、图3( $1 A 1 B$ )的方式放置在同一个含 $60^{°}$ 内角的菱形中.若知道图形②与图形⑤的面积差.则一定能求出（）

A、图形①与图形③的周长和 B、图形④与图形⑥的周长和 C、图形①与图形③的周长差 D、图形④与图形⑥的周长差

查看试题解析
10. 如图，已知四边形 $A B C D$ 是矩形，点 $M$ 在 $B C$ 上， $B M = C D$ ，点 $N$ 在 $C D$ 上，且 $D N = C M ， D M$ 与 $B N$ 交于点 $P$ ，则 $D M ： B N =$ （）

A、 $\sqrt{3} ： 2$ B、 $1 ： \sqrt{2}$ C、 $\sqrt{2} ： \sqrt{3}$ D、 $2 ： \sqrt{5}$

查看试题解析

二、填空题

11. 二次根式 $\sqrt{1 - 3 x}$ 中x的取值范围是．

查看试题解析
12. 已知一个多边形的每一个外角都等于72°，则这个多边形的边数是.

查看试题解析
13. 二次函数 $y = {(x - 1)}^{2} + 1$ 的图象先向右平移 $2$ 个单位，再向上平移 $3$ 个单位，平移后图象的函数表达式为.

查看试题解析
14. 小明用 $s^{2} = \frac{1}{10} [{(x_{1} - 3)}^{2} + {(x_{2} - 3)}^{2} + \cdot \cdot \cdot + {(x_{10} - 3)}^{2}]$ 计算一组数据的方差，那么 $x_{1} + x_{2} + x {}_{3}+ \dots + x_{10}$ ＝.

查看试题解析
15. 已知：如图，点 $B$ 、点 $C$ 是反比例函数 $y = \frac{6 \sqrt{2}}{x} (x > 0)$ 图象上的两点，过点 $C$ 作 $C D ⊥ x$ 轴于点 $D$ .过点 $B$ 作 $B A ⊥ x$ 轴于点 $A$ ，连接 $O C$ ，交 $A B$ 于点 $E$ ，连接 $O B 、 B C .$ 当 $A$ 为 $O D$ 中点且 $∠ O B C = 90^{°}$ 时，点 $C$ 的坐标为.

查看试题解析
16. 已知：如图，在矩形 $A B C D$ 中， $A B = 3 ， A D = 4$ .动点 $P$ 为矩形 $A B C D$ 内一点，且满足 $S_{Δ P B C} = \frac{1}{3} S_{矩形 A B C D}$ ，则 $△ A D P$ 周长的最小值为.

查看试题解析

三、解答题

17. 计算

(1)、 $\sqrt{2} (\frac{\sqrt{8}}{3} - \sqrt{2} + \sqrt{\frac{1}{2}})$

(2)、 $\sqrt{{(- 5)}^{2}} - (\sqrt{3} + 1) (\sqrt{3} - 1) + \sqrt{0.01}$

查看试题解析
18. 用适当的方法解下列方程：

(1)、 $2 {(x - 2)}^{2} = x - 2$

(2)、 $x^{2} - 10 x + 8 = 0$

查看试题解析
19. 已知：如图，在四边形 $A B C D$ 中， $A B / / C D$ .点 $E ， F$ 在对角线 $A C$ 上，且 $A E = C F ， D F / / B E$ ，

(1)、求证： $△ A B E ≅ △ C D F$ ；

(2)、连接 $B D$ ，交 $A C$ 于点 $O$ ，若 $B D ⊥ A C$ ，四边形 $A B C D$ 周长为 $16 ， A C = 4 \sqrt{3}$ ，求 $∠ D A B$ 的大小.

查看试题解析
20. 为进一步提升校园阅读氛围，在第24个“世界读书日”之际，学校开展了“读书四月，书香满园”的主题活动.活动结束后学生会随机调查了45名学生四月读书月课外阅读时间（单位：小时）的样本数据，结果统计如下：

四月课外阅读时间（小时)

9

10

11

12

13

人数

7

11

10

9

8

(1)、求出上述样本数据的众数、中位数及平均数；

(2)、若该校学生人数为 $540$ 人，请估计四月课外阅读时间达到 $12$ 小时及以上的学生人数约为多少人.

查看试题解析
21. 已知：如图，在平面直角坐标系中，一次函数 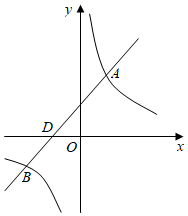$y = x + 1$ 与反比例函数 $y = \frac{a}{x} (a \neq 0)$ 的图象交于点 $A (2 ， m)$ 和点 $B$ ，与 $x$ 轴交于点 $D$ ，

(1)、求 $a ， m$ 的值及点 $B$ 的坐标；

(2)、写出 $x + 1 - \frac{a}{x} \leq 0$ 时 $x$ 的取值范围；

(3)、 $P$ 是 $x$ 轴上一点，且满足 $△ P A B$ 的面积等于 $5$ .求点 $P$ 坐标.

查看试题解析
22. 夏天到了，宁波人最惦记的水果——杨梅进入成熟期，一水果店老板进行杨梅销售，已知杨梅进价为25元/千克.如果售价为30元/千克，那么每天可售出150千克：如果售价为32元/千克，那么每天可售出130千克.经调查发现：每天销售量 $y$ (千克）与售价 $x$ (元/千克)之间存在一次函数关系.

(1)、求出 $y$ 关于 $x$ 的一次函数关系式；

(2)、若杨梅售价不得高于36元/千克，该店主销售杨梅每天要获得960元的毛利润，则销售单价应定为多少元/千克?（毛利润=销售额-进货成本〉

(3)、设杨梅每天销售的毛利润为 $W$ 元，当杨梅的售价定为多少元/千克时，每天销售获得的毛利润最大?最大毛利润是多少元?

查看试题解析
23. 定义：如果一个凸四边形有三条边相等，那么称这个凸四边形为“准等边四边形”.如正方形就是一个“准等边四边形”.

(1)、如图，在给定的网格中，找到格点 $D$ .使得以 $A 、 B 、 C 、 D$ 为顶点的四边形是准等边四边形，请按要求画两个且不全等的准等边四边形.

(2)、如图1， $▱ A B C D$ 中，对角线 $C A$ 平分 $∠ B C D$ ，将线段 $C D$ 绕点 $C$ 顺时针方向旋转一个角度 $α (0 < α < ∠ B)$ 至 $C E$ ，连接 $A E 、 D E ，$

①求证：四边形 $A B C E$ 是准等边四边形；

②如图2，连接BE，求证： $∠ B E D = ∠ A C B$ ；

(3)、如图3，在准等边四边形 $A B C D$ 中， $A B = B C = C D = 2 ， ∠ B C D = 90^{°} ， ∠ B = 150^{°}$ ，请求出 $∠ B A D$ 的大小及该四边形的面积.

查看试题解析
24. 在平面直角坐标系中，已知 $A (0 ， 4)$ ，点 $B (m ， 4)$ ，点 $B$ 落在第二象限，点 $D$ 是 $y$ 轴正半轴上一动点，

(1)、如图1，当 $m = - 2$ 时，将 $△ B O D$ 沿着直线 $B D$ 翻折，点 $O$ 落在第一象限的点 $E$ 处.
①若 $B E / / x$ 轴，求点 $E$ 的坐标；

②如图2，当点 $D$ 运动到 $O A$ 中点时，连接 $A E$ ，请判断四边形 $A B D E$ 的形状，并说明理由；

③如图3，在折叠过程中，是否存在点 $D$ ，使得 $△ O A E$ 是以 $O A 、 O E$ 为腰的等暖三角形﹖若存在，求出对应 $D$ 点的坐标.若不存在.请说明理由；

(2)、如图4，将 $△ A B O$ 沿着 $O B$ 翻折.得到 $△ F B O$ .(点 $A$ 的对应点为点 $F$ )，若点 $F$ 到 $x$ 轴的距离不大于 $3$ ，直接写出 $m$ 的取值范围.（不需要解答过程)

查看试题解析

四月课外阅读时间（小时)	9	10	11	12	13
人数	7	11	10	9	8