初中数学北师大版九年级上学期 第一章 单元测试卷
试卷更新日期：2021-07-23 类型：单元试卷
一、单选题
-
1. 正方形､菱形､矩形都具有的性质是（ ）A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角线平分一组对角2. 如图，在反映特殊四边形之间关系的知识结构图中，①②③④表示需要添加的条件，则下列描述错误的是（ ）
A、①表示有一个角是直角 B、②表示有一组邻边相等 C、③表示四个角都相等 D、④表示对角线相等3. 已知菱形 中，对角线 与 交于点O， ， ，则该菱形的周长是（ ）
A、13 B、52 C、120 D、2404. 若菱形的周长为16，高为2，则菱形两邻角的度数之比为（ ）A、4：1 B、5：1 C、6：1 D、7：15. 已知 中，下列条件：① ；② ；③ ；④ 平分 ，其中能说明 是矩形的是（ ）A、① B、② C、③ D、④6. 如图，菱形ABCD中，AC交BD于点O ， DE⊥BC于点E ， 连接OE ， 若∠ABC＝140°，则∠OED＝（ ）
A、20° B、30° C、40° D、50°7. 将边长分别为2和4的长方形如图剪开，拼成一个正方形，则该正方形的边长最接近整数（ ）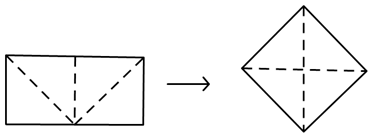
A、1 B、2 C、3 D、48. 如图，在正方形 中，点 是 的中点，点 是 的中点， 与 相交于点 ，设 .得到以下结论：① ；② ；③ 则上述结论正确的是（ ）
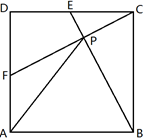A、①② B、①③ C、②③ D、①②③二、填空题
-
9. 菱形ABCD中，对角线AC长为10cm，BD＝6cm，则菱形ABCD的面积为cm2.10. 菱形ABCD的对角线AC与BD相交于点O，BD：AC＝4：3，菱形ABCD的周长为40，则菱形ABCD的面积为.11. 正方形 的对角线长为 ，面积为.12. 如图，菱形 的对角线 ， 相交于点 ，已知 ，菱形 的面积为24，则 的长为.
13. 如图，O点是矩形ABCD的对角线AC的中点，菱形ABEO的边长为2，则BC＝ ．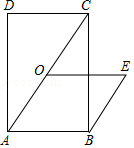
14. 把图1中边长为10的菱形沿对角线分成四个全等的直角三角形，且此菱形的一条对角线长为16，将这四个直角三角形拼成如图2所示的正方形，则图2中的阴影的面积为 ．
15. 如图，在平面直角坐标系xOy中，点A、C、F在坐标轴上，E是OA的中点，四边形AOCB是矩形，四边形BDEF是正方形，若点C的坐标为 ，则点E的坐标为 ．
16. 如图，四边形ABCD是菱形，∠BAD=60°，AB=6，对角线AC与BD相较于点O，点E在AC上，若OE=2 ，则CE的长为
三、解答题
-
17. 如图，已知菱形ABCD，延长AD到点F，使 ，延长CD到点E，使DE=CD，顺次连接点A，C，F，E，A．求证：四边形ACFE是矩形.
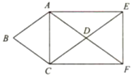18. 如图，已知四边形ABCD是菱形，DE⊥AB，DF⊥BC，求证：△ADE≌△CDF．
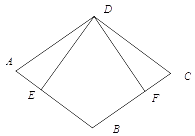19. 如图，矩形 的对角线 ， 交于点 ，且 ， ，连接 .求证： .
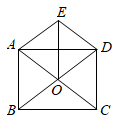20. 如图，已知四边形ABCD是矩形，点E在对角线AC上，点F在边CD上（点F与点C、D不重合）， ，且 .求证：四边形ABCD是正方形.
21. 如图，在 中， ， 是 边上的中线，过点B作 ，过点C作 ， ， 相交于点E．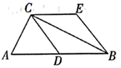
求证：四边形 是菱形．
22. 如图，延长矩形 的边 至点E，使 ，连接 ， ，求证： 平分 ．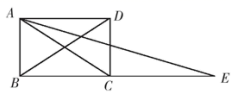
23. 如图，四边形ABCD为矩形，点E为边AB上一点，连接DE并延长，交CB的延长线于点P ， 连接PA ， ∠DPA＝2∠DPC ． 求证：DE＝2PA ．
24.(1)、基础探究：如图①，在正方形ABCD中，点E为AD上一点，DF⊥CE交AB于F，垂足为点O．求证：CE＝DF．
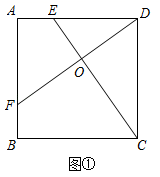(2)、应用拓展：如图②，在正方形ABCD中，点E为AD上一点，FG⊥CE分别交AB、CD于F、G，垂足为点O．若正方形ABCD的边长为12，DE＝5，则四边形EFCG的面积为 ．
25.已知正方形ABCD，P为射线AB上的一点，以BP为边作正方形BPEF，使点F在线段CB的延长线上，连接EA，EC．
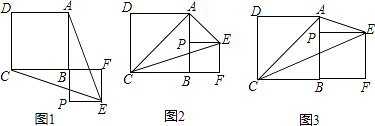
（Ⅰ）如图1，若点P在线段AB的延长线上，求证：EA=EC；
（Ⅱ）如图2，若点P在线段AB的中点，连接AC，判断△ACE的形状，并说明理由；
（Ⅲ）如图3，若点P在线段AB上，连接AC，当EP平分∠AEC时，设AB=a，BP=b，求a：b及∠AEC的度数．