浙江省宁波市鄞州区2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-07-23 类型:期末考试
一、单选题
-
1. 一元二次方程 的二次项系数是( )A、1 B、2 C、-2 D、32. 下列计算正确的是( )A、 B、 C、 D、3. 下列图标中,属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 矩形 中,对角线 与 相交于点O,若 , ,则对角线 的长是( )A、3 B、 C、 D、65. 用配方法解方程 ,下列变形正确的是( )A、 B、 C、 D、6. 在一次射击比赛中,某位选手前5次的成绩的环数分别为:8,7,4,7,9,若他第6次的射击成绩为7环,则前后两组数据中,变化的统计量是( )A、众数 B、中位数 C、平均数 D、方差7. 用反证法证明命题“在△ABC中,若AB>AC,则∠C>∠B”时,第一步应假设( )A、∠C<∠B B、∠C≤∠B C、AB<AC D、AB≤AC8. 如图, 的顶点A是双曲线 上的动点,过点A作 轴交双曲线 于点C,顶点B在y轴上,下列说法正确的是( )
4. 矩形 中,对角线 与 相交于点O,若 , ,则对角线 的长是( )A、3 B、 C、 D、65. 用配方法解方程 ,下列变形正确的是( )A、 B、 C、 D、6. 在一次射击比赛中,某位选手前5次的成绩的环数分别为:8,7,4,7,9,若他第6次的射击成绩为7环,则前后两组数据中,变化的统计量是( )A、众数 B、中位数 C、平均数 D、方差7. 用反证法证明命题“在△ABC中,若AB>AC,则∠C>∠B”时,第一步应假设( )A、∠C<∠B B、∠C≤∠B C、AB<AC D、AB≤AC8. 如图, 的顶点A是双曲线 上的动点,过点A作 轴交双曲线 于点C,顶点B在y轴上,下列说法正确的是( )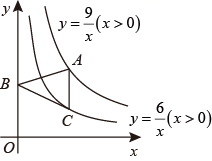 A、 的周长存在最大值 B、 的面积存在最小值 C、 的周长始终不变 D、 的面积始终不变9. 如图,四边形 中, , , ,点M是对角线 的中点,点N是 边的中点,连结 , ,若 ,则线段 的长是( )
A、 的周长存在最大值 B、 的面积存在最小值 C、 的周长始终不变 D、 的面积始终不变9. 如图,四边形 中, , , ,点M是对角线 的中点,点N是 边的中点,连结 , ,若 ,则线段 的长是( )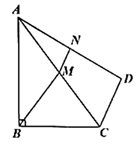 A、 B、3 C、 D、510. 如图,在正方形 中,点P在对角线 上, , ,E,F分别为垂足,连结 , ,则下列命题:①若 ,则 ;②若 ,则 ;③若正方形边长为4,则 的最小值为2,其中正确的命题是( )
A、 B、3 C、 D、510. 如图,在正方形 中,点P在对角线 上, , ,E,F分别为垂足,连结 , ,则下列命题:①若 ,则 ;②若 ,则 ;③若正方形边长为4,则 的最小值为2,其中正确的命题是( )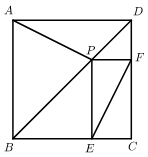 A、①② B、①③ C、②③ D、①②③
A、①② B、①③ C、②③ D、①②③二、填空题
-
11. 二次根式 中字母x的取值范围是_ 。12. 如果一个正多边形的每个内角为150°,则这个正多边形的边数是 .13. 若m是方程 的一个根,则 的值为.14. 某班在一次数学考试中,“乘风组”的平均成绩为80分,“破浪组”的平均成绩为86分.若“乘风组”人数是“破浪组”的2倍,则该班此次数学考试的平均成绩是.15. 如图,在菱形 中,E,F分别在 , 上, , ,若 ,则 的度数是.
 16. 如图,矩形 的顶点A在y轴的正半轴上,顶点C在x轴的正半轴上,反比例函数 在第一象限内的图象分别与边 、 相交于点D、E.连结 , ,恰有 , ,若 ,则k的值是.
16. 如图,矩形 的顶点A在y轴的正半轴上,顶点C在x轴的正半轴上,反比例函数 在第一象限内的图象分别与边 、 相交于点D、E.连结 , ,恰有 , ,若 ,则k的值是.
三、解答题
-
17. 计算:(1)、(2)、18. 解方程:(1)、(2)、19. 据悉某市即将建设海上风电项目,需要铺设一条海底电缆,项目方从甲、乙两厂中分别选取6根不同批次的电缆检测载流量,数据统计如下(抽样数据单位:千安).
甲、乙两厂电缆载流量统计表
电缆
一
二
三
四
五
六
平均数
中位数
众数
方差
甲厂
1.6
1.6
1.3
0.7
1.3
1.3
a
1.3
1.3
0.09
乙厂
0.7
1.5
1.5
1.3
1.5
1.3
1.3
b
c
0.08
(1)、补全表中数据, , , ;(2)、若优质的电缆是有较高的载流量且性能稳定,请你结合表中数据,帮助项目方选择合适的电缆厂家,并写出两条推荐理由.20. 如图,一次函数 的图象与反比例函数 的图象交于点A,B,过点A作 轴,垂足为点H,连结 .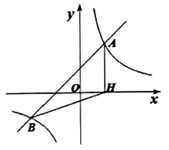 (1)、求点A,B的坐标和 的面积;(2)、当 时,请利用图象直接写出自变量x的取值范围.21. 如图,将矩形纸片 的四个角向内折叠,恰好拼成一个无缝隙、无重叠的四边形 .
(1)、求点A,B的坐标和 的面积;(2)、当 时,请利用图象直接写出自变量x的取值范围.21. 如图,将矩形纸片 的四个角向内折叠,恰好拼成一个无缝隙、无重叠的四边形 . (1)、求证:四边形 是矩形;(2)、若 , ,求四边形 的面积.22. 随着“共享经济”的概念迅速普及,共享汽车也进入了人们的视野,某共享汽车租赁公司年初在某地投放了一批共享汽车,全天包车的租金定为每辆120元.据统计,三月份的全天包车数为25次,在租金不变的基础上,四、五月的全天包车数持续走高,五月份的全天包车数达到64次.(1)、若从三月份到五月份的全天包车数月平均增长率不变,求全天包车数的月平均增长率;(2)、从六月份起,该公司决定降低租金,经调查发现,租金每降价a元,全天包车数增加 次,当租金降价多少元时,公司将获利8800元?23. 我们定义:有一组对边相等,另一组对边不相等的凸四边形叫做“单等对边四边形”.
(1)、求证:四边形 是矩形;(2)、若 , ,求四边形 的面积.22. 随着“共享经济”的概念迅速普及,共享汽车也进入了人们的视野,某共享汽车租赁公司年初在某地投放了一批共享汽车,全天包车的租金定为每辆120元.据统计,三月份的全天包车数为25次,在租金不变的基础上,四、五月的全天包车数持续走高,五月份的全天包车数达到64次.(1)、若从三月份到五月份的全天包车数月平均增长率不变,求全天包车数的月平均增长率;(2)、从六月份起,该公司决定降低租金,经调查发现,租金每降价a元,全天包车数增加 次,当租金降价多少元时,公司将获利8800元?23. 我们定义:有一组对边相等,另一组对边不相等的凸四边形叫做“单等对边四边形”.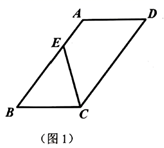
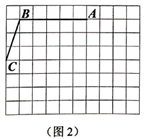
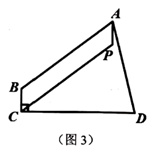 (1)、如图1,在 中,点E为 上不与点A,B重合的一点, .求证:四边形 为单等对边四边形;(2)、如图2,在 的网格中,顶点A、B、C均是格点,请在此网格内找格点D,使四边形 为单等对边四边形,请你在网格中画出所有满足条件的点D;(3)、如图3,在单等对边四边形 中, , , , ,若单等对边四边形 内有一点P,使四边形 为平行四边形,且 与四边形 的面积比为 ,求 的面积.
(1)、如图1,在 中,点E为 上不与点A,B重合的一点, .求证:四边形 为单等对边四边形;(2)、如图2,在 的网格中,顶点A、B、C均是格点,请在此网格内找格点D,使四边形 为单等对边四边形,请你在网格中画出所有满足条件的点D;(3)、如图3,在单等对边四边形 中, , , , ,若单等对边四边形 内有一点P,使四边形 为平行四边形,且 与四边形 的面积比为 ,求 的面积.