浙江省杭州市西湖区2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-07-23 类型:期末考试
一、单选题
-
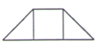
1. ( )A、-4 B、2 C、4 D、82. 将七巧板的其中几块拼成一个多边形为中心对称图形的是( )A、
 B、
B、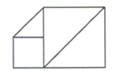 C、
C、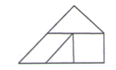 D、
D、 3. 有15名学生参加学校举办的“最强大脑”智力竞赛,比赛结束后根据每个学生的成绩计算平均数、中位数、众数、方差,若去掉一个最高分,一个最低分,则一定不会发生变化的是( )A、平均数 B、中位数 C、众数 D、方差4. 下列方程中有两个相等实数根的是( )A、 B、 C、 D、5. 若反比例函数 的图象经过点 ,则它的图象一定还经过点( )A、 B、 C、 D、6. 如图所示,将正五边形ABCDE的点C固定,并按顺时针方向旋转,要使新五边形A′B′CD′E′的顶点D′落在直线BC上,则旋转角度为( )
3. 有15名学生参加学校举办的“最强大脑”智力竞赛,比赛结束后根据每个学生的成绩计算平均数、中位数、众数、方差,若去掉一个最高分,一个最低分,则一定不会发生变化的是( )A、平均数 B、中位数 C、众数 D、方差4. 下列方程中有两个相等实数根的是( )A、 B、 C、 D、5. 若反比例函数 的图象经过点 ,则它的图象一定还经过点( )A、 B、 C、 D、6. 如图所示,将正五边形ABCDE的点C固定,并按顺时针方向旋转,要使新五边形A′B′CD′E′的顶点D′落在直线BC上,则旋转角度为( ) A、108° B、72° C、54° D、36°7. 某口罩生产厂2020年1月份平均日产20万个,1月底因防控新冠疫情需求,工厂立即决定从2月份起扩大产能,3月份平均日产量达到45万个,则口罩日产量的月平均增长率是( )A、20% B、30% C、40% D、50%8. 在菱形 中,记 ,菱形的面积记作S,菱形的周长记作L.若 ,则( )A、L与 的大小有关 B、当 时, C、S随 的增大而增大 D、S随 的增大而减小9. 已知关于x的一元二次方程 有两个不相等的实数根,设此方程的一个实数根为b,令 ,则( )A、 B、 C、 D、10. 如图,矩形 中,E,F是 上的两个点, , ,垂足分别为G,H,若 , , ,且 ,则 ( )
A、108° B、72° C、54° D、36°7. 某口罩生产厂2020年1月份平均日产20万个,1月底因防控新冠疫情需求,工厂立即决定从2月份起扩大产能,3月份平均日产量达到45万个,则口罩日产量的月平均增长率是( )A、20% B、30% C、40% D、50%8. 在菱形 中,记 ,菱形的面积记作S,菱形的周长记作L.若 ,则( )A、L与 的大小有关 B、当 时, C、S随 的增大而增大 D、S随 的增大而减小9. 已知关于x的一元二次方程 有两个不相等的实数根,设此方程的一个实数根为b,令 ,则( )A、 B、 C、 D、10. 如图,矩形 中,E,F是 上的两个点, , ,垂足分别为G,H,若 , , ,且 ,则 ( )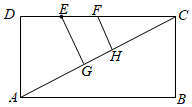 A、 B、 C、3 D、
A、 B、 C、3 D、二、填空题
-
11. 若 在实数范围内有意义,则实数 的取值范围是.12. 方程 的解是.13. 已知一组数据:5,2,5,6,7,则这组数据的方差是.14. 如图,在 中,点D,E分别是 , 的中点,连结 ,若 , , ,则BE=.
 15. 在直角坐标系中,已知直线 与反比例函数 的图象交于点 , ,则 .16. 如图,矩形 中, , ,连结对角线 ,E为 的中点,F为 边上的动点连结 ,作点C关于 的对称点 ,连结 , ,若 与 的重叠部分( )面积等于 的 ,则 .
15. 在直角坐标系中,已知直线 与反比例函数 的图象交于点 , ,则 .16. 如图,矩形 中, , ,连结对角线 ,E为 的中点,F为 边上的动点连结 ,作点C关于 的对称点 ,连结 , ,若 与 的重叠部分( )面积等于 的 ,则 .
三、解答题
-
17. 请比较 和 的大小.18. 某区要举办中学生科普知识竞赛,我校要选拔一支代表队参赛.选拔赛满分为100分,规定85分及以上为“合格”,95分及以上为“优秀”.现将A,B两支预选队的竞赛成绩统计如下:

组别
队
队
平均分
88
87
中位数
90
a
方差
61
71
合格率
70%
b
优秀率
30%
25%
(1)、求出表中a,b的值(2)、若从A,B两队中选取成绩前20名(包括第20名)的学生组成代表队,小明的成绩正好是本队成绩的中位数,但他却落选了,那么小明应属于哪个队?请说明理由.19. 某小区有一块边长为a的正方形场地,规划修建两条宽为b的绿化带(即图中阴影部分).方案一如图甲所示,绿化带面积为 ;方案二如图乙所示,绿化带面积为 . (1)、请用含a,b的代数式表示 和 .(2)、设 ,求k的取值范围.20. 已知 .(1)、当 时,求x的值.(2)、若 ,求M的值.(3)、求证: .21. 如图, , 为平行四边形 的对角线,点E是 上一点,点F在 延长线
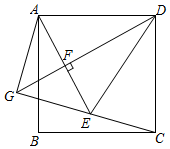
(1)、请用含a,b的代数式表示 和 .(2)、设 ,求k的取值范围.20. 已知 .(1)、当 时,求x的值.(2)、若 ,求M的值.(3)、求证: .21. 如图, , 为平行四边形 的对角线,点E是 上一点,点F在 延长线上,且 , 与 交于点G,连结 .
 (1)、求证: .(2)、连结 , ,若 ,且G恰好是 的中点,求证:四边形 是菱形.(3)、在(2)的条件下,若四边形 是正方形,且 ,求 的长.
(1)、求证: .(2)、连结 , ,若 ,且G恰好是 的中点,求证:四边形 是菱形.(3)、在(2)的条件下,若四边形 是正方形,且 ,求 的长.