河南省商丘市睢阳区2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-07-23 类型:期末考试
一、单选题
-
1. 下列各式是二次根式的是( )A、 B、 C、 D、2. 下列各曲线中,表示y是x的函数的是( )A、
 B、
B、 C、
C、 D、
D、 3. 甲、乙、丙、丁四个小组的同学分别参加了班里组织的中华古诗词知识竞赛,四个小组的平均分相同,若要从中选择出一个各成员实力更平均的小组参加年级的比赛,那么应选( )
3. 甲、乙、丙、丁四个小组的同学分别参加了班里组织的中华古诗词知识竞赛,四个小组的平均分相同,若要从中选择出一个各成员实力更平均的小组参加年级的比赛,那么应选( )甲
乙
丙
丁
方差
3.6
3.2
4
4.3
A、甲组 B、乙组 C、丙组 D、丁组4. 下列各式中,计算正确的是( )A、 B、 C、 D、5. 一个门框的尺寸如图所示,下列长×宽型号(单位:m)的长方形薄木板能从门框内通过的是( ) A、 B、 C、 D、6. 如图,在四边形 中,对角线 , 相交于点 ,且 ,OB=OD,下列结论不一定成立的是( )
A、 B、 C、 D、6. 如图,在四边形 中,对角线 , 相交于点 ,且 ,OB=OD,下列结论不一定成立的是( )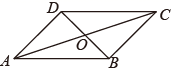 A、 B、 C、 D、7. 如图,平行四边形 的顶点O , A , C的坐标分别是 ,则顶点B的坐标是( )
A、 B、 C、 D、7. 如图,平行四边形 的顶点O , A , C的坐标分别是 ,则顶点B的坐标是( ) A、 B、 C、 D、8. 为庆祝中国共产党建党100周年,某校开展了以“学党史知识迎建党百年”为主题的党史知识竞赛,并将所有参赛学生的成绩进行统计整理,绘制成如下统计图 (每个小组含前一个边界值,不含后一个边界值).根据图中的信息判断:关于这次知识竞赛成绩的中位数的结论正确的是( )
A、 B、 C、 D、8. 为庆祝中国共产党建党100周年,某校开展了以“学党史知识迎建党百年”为主题的党史知识竞赛,并将所有参赛学生的成绩进行统计整理,绘制成如下统计图 (每个小组含前一个边界值,不含后一个边界值).根据图中的信息判断:关于这次知识竞赛成绩的中位数的结论正确的是( ) A、中位数在60分~70分之间 B、中位数在70分~80分之间 C、中位数在80分~90分之间 D、中位数在90分~100分之间9. 如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是( )
A、中位数在60分~70分之间 B、中位数在70分~80分之间 C、中位数在80分~90分之间 D、中位数在90分~100分之间9. 如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是( ) A、1,4,5 B、2,3,5 C、3,4,5 D、2,2,410. 已知某四边形的两条对角线相交于点O.动点P从点A出发,沿四边形的边按A→B→C的路径匀速运动到点C.设点P运动的时间为x,线段OP的长为y,表示y与x的函数关系的图象大致如图所示,则该四边形可能是( )
A、1,4,5 B、2,3,5 C、3,4,5 D、2,2,410. 已知某四边形的两条对角线相交于点O.动点P从点A出发,沿四边形的边按A→B→C的路径匀速运动到点C.设点P运动的时间为x,线段OP的长为y,表示y与x的函数关系的图象大致如图所示,则该四边形可能是( ) A、
A、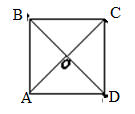 B、
B、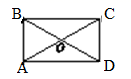 C、
C、 D、
D、
二、填空题
-
11. 化简二次根式: , .12. 如图,将直线OA向上平移1个单位,得到一个一次函数的图象,那么这个一次函数的关系式是 .
 13. 某商场为了招聘商品拆装上架员工一名,设置了计算机、语言和商品知识三项测试,并对这三项测试成绩按照2:3:5的比确定.若某应试者三项测试成绩分别为70,50,80,则该应试者的平均成绩是.14. 如图,台阶阶梯每一层高 ,宽 ,长 .一只蚂蚁从 点爬到 点,最短路程是.
13. 某商场为了招聘商品拆装上架员工一名,设置了计算机、语言和商品知识三项测试,并对这三项测试成绩按照2:3:5的比确定.若某应试者三项测试成绩分别为70,50,80,则该应试者的平均成绩是.14. 如图,台阶阶梯每一层高 ,宽 ,长 .一只蚂蚁从 点爬到 点,最短路程是. 15. 阅读下面材料:
15. 阅读下面材料:在数学课上,老师提出如下问题:
尺规作图:作对角线等于已知线段的菱形.
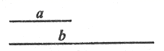 已知:两条线段a、b.
已知:两条线段a、b.求作:菱形AMBN,使得其对角线分别等于b和2a.
小军的作法如下:
如图
(1)画一条线段AB等于b;
(2)分别以A、B为圆心,大于 AB的长为半径,
在线段AB的上下各作两条弧,两弧相交于P、Q两点;
(3)作直线PQ交AB于O点;
(4)以O点为圆心,线段a的长为半径作两条弧,交直线PQ于M、N两点,连接AM、AN、BM、BN.所以四边形AMBN就是所求的菱形.
老师说:“小军的作法正确.”
该上面尺规作图作出菱形AMBN的依据是

三、解答题
-
16.(1)、计算: ;(2)、先化简,再求值: ,其中 , .17. 如图,在平面直角坐标系xOy中,已知点A(﹣1,5),B(1,0),C(3,1),连接BC.
 (1)、在图中画出点A关于y轴的对称点 ,连接 ,并直接写出点 的坐标;(2)、在(1)的基础上,试判断△ 的形状,并说明理由.18. 如图,在平行四边形 中,对角线 , 交于点 ,过点 作 于点 ,延长 至 ,使 ,连接 .
(1)、在图中画出点A关于y轴的对称点 ,连接 ,并直接写出点 的坐标;(2)、在(1)的基础上,试判断△ 的形状,并说明理由.18. 如图,在平行四边形 中,对角线 , 交于点 ,过点 作 于点 ,延长 至 ,使 ,连接 . (1)、求证:四边形 是矩形.(2)、若四边形 是菱形, , ,求矩形 的面积.19. 某植物 天后的高度为 , 反映了 与 之间的关系.根据图象回答下列问题:
(1)、求证:四边形 是矩形.(2)、若四边形 是菱形, , ,求矩形 的面积.19. 某植物 天后的高度为 , 反映了 与 之间的关系.根据图象回答下列问题: (1)、求3天后该植物高度为多少?(2)、图象对应的一次函数 中, 和 的实际意义分别是什么?20. 甲、乙两人在“定位投篮”选拔赛测试中(共10轮,每轮投10个球)成绩如下:
(1)、求3天后该植物高度为多少?(2)、图象对应的一次函数 中, 和 的实际意义分别是什么?20. 甲、乙两人在“定位投篮”选拔赛测试中(共10轮,每轮投10个球)成绩如下: (1)、填表:
(1)、填表:平均数
中位数
众数
方差
甲
7.5
8
乙
7
1.2
(2)、如果你是教练,你会选择谁参加正式比赛?请说明理由.21. 小明和小亮进行百米赛跑,小明比小亮跑得快.如果两人同时起跑,小明肯定赢.现在小明让小亮先跑若干米.图中 , ,分别表示两人的路程与小明追赶时间的关系. (1)、哪条线表示小明的路程与时间之间的关系?(2)、小明让小亮先跑了多少米?(3)、谁将赢得这场比赛?22. 某学校拟购进甲、乙两种规格的书柜放置新购买的图书.已知每个甲种书柜的进价比每个乙种书柜的进价高20%,用5400元购进的甲种书柜的数量比用6300元购进乙种书柜的数量少6个.(1)、每个甲种书柜的进价是多少元?(2)、若该校拟购进这两种规格的书柜共60个,其中乙种书柜的数量不大于甲种书柜数量的 倍.该校应如何进货使得购进书柜所需费用最少?23. 阅读与思考:
(1)、哪条线表示小明的路程与时间之间的关系?(2)、小明让小亮先跑了多少米?(3)、谁将赢得这场比赛?22. 某学校拟购进甲、乙两种规格的书柜放置新购买的图书.已知每个甲种书柜的进价比每个乙种书柜的进价高20%,用5400元购进的甲种书柜的数量比用6300元购进乙种书柜的数量少6个.(1)、每个甲种书柜的进价是多少元?(2)、若该校拟购进这两种规格的书柜共60个,其中乙种书柜的数量不大于甲种书柜数量的 倍.该校应如何进货使得购进书柜所需费用最少?23. 阅读与思考:正方形还有许多有趣的性质,下面是小宇同学找到的有关正方形的几个图形,想一想其中的道理.

如图①,在正方形 中,点 、 、 分别是边 、 , 上的点.
(1)、解决问题:如图④,在正方形 中,点 在边 上(点 与点 、 不重合),过点 作 , 与边 相交于点 ,与边 的延长线相交于点 .
猜想线段 、 、 的数量关系是 , 并证明你的猜想; (2)、连接 ,如果正方形的边长为2,设 , 的面积为 ,直接写出 与 之间的关系式,并写出自变量 的取值范围.(3)、获得发现:如图①,当 时,则有 ;如图②,当 时,则有 ;如图③,当 时,则有 .想一想,这是为什么?结合图②给出证明.
(2)、连接 ,如果正方形的边长为2,设 , 的面积为 ,直接写出 与 之间的关系式,并写出自变量 的取值范围.(3)、获得发现:如图①,当 时,则有 ;如图②,当 时,则有 ;如图③,当 时,则有 .想一想,这是为什么?结合图②给出证明.