河南省商丘市梁园区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-07-23 类型：期末考试

进入出卷网下载

一、单选题

1. 在▱ABCD中，如果 $∠ A = 65^{\circ}$ ，那么 $∠ C$ 的度数是（）

A、115º B、65º C、25º D、35º

查看试题解析
2. 如图，在 $Δ A B C$ 中， $A C = 4$ ，点 $D$ ， $E$ 分别是边 $A B$ ， $C B$ 的中点，那么 $D E$ 的长为 $($ $)$

A、2 B、1.5 C、4 D、3

查看试题解析
3. 在 $Δ A B C$ 中， $∠ A$ ， $∠ B$ ， $∠ C$ 的对边分别是a，b，c，下列条件中，不能判定 $Δ A B C$ 是直角三角形的是（）

A、 $∠ A + ∠ B = 90^{°}$ B、 $∠ A + ∠ B = ∠ C$ C、 $a = 1$ ， $b = 3$ ， $c = \sqrt{10}$ D、 $a : b : c = 1 : 2 : 2$

查看试题解析
4. 下列运算正确的是 $($ $)$

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{3} \times \sqrt{5} = 15$ C、 $3 \sqrt{2} - \sqrt{2} = 3$ D、 $\sqrt{24} \div \sqrt{3} = 2 \sqrt{2}$

查看试题解析
5. 下列函数的图象 $y$ 随 $x$ 的增大而减小的是（）

A、 $y = 2 x$ B、 $y = 3 x + 1$ C、 $y = 4 x - 1$ D、 $y = - 2 x + 1$

查看试题解析
6. 如图，数轴上点A，B分别对应1，2，过点B作PQ⊥AB，以点B为圆心，AB长为半径画弧，交PQ于点C，以点A为圆心，AC长为半径画弧，交数轴于点M，则点M对应的数是（）

A、 $\sqrt{2}$ B、 $\sqrt{5}$ C、 $\sqrt{2}$ +1 D、 $\sqrt{5}$ +1

查看试题解析
7. 如图，平行四边形ABCD的对角线相交于点O，且AD≠CD，过点0作OM⊥AC，交AD于点M.如果△CDM的周长为8，那么平行四边形ABCD的周长是（）

A、8 B、12 C、16 D、20

查看试题解析
8. 小丽在本学期的数学成绩分别为：平时测验成绩为93分，期中考试成为90分，期末考试成绩为95分，按照平时、期中、期末所占比例为10%，30%，60%计算小丽本学期的总评成绩应该是（）

A、92.5分 B、92.8分 C、93.1分 D、93.3分

查看试题解析
9. 如图，直线 $y = - x + m$ 与 $y = n x + 4 n (n \neq 0)$ 的交点的横坐标为-2，则关于 $x$ 的不等式 $- x + m > n x + 4 n > 0$ 的整数解为（）.

A、-1 B、-5 C、-4 D、-3

查看试题解析
10. 如图，在平面直角坐标系中，点 $A_{1}$ ， $A_{2}$ ， $A_{3}$ 在直线 $y = \frac{1}{5} x + b$ 上，点 $B_{1}$ ， $B_{2}$ ， $B_{3}$ 在x轴上， $Δ O A_{1} B_{1}$ ， $Δ B_{1} A_{2} B_{2}$ ， $Δ B_{2} A_{3} B_{3}$ 都是等腰直角三角形，若已知点 $A_{1} (1 ， 1)$ ，则点 $A_{3}$ 的纵坐标是（）

A、 $\frac{3}{2}$ B、 $\frac{2}{3}$ C、 $\frac{4}{9}$ D、 $\frac{9}{4}$

查看试题解析

二、填空题

11. 函数 $y = \sqrt{x - 3}$ 中，自变量x的取值范围是．

查看试题解析
12. 一组数据2，0，1，x，3的平均数是2，则这组数据的方差是.

查看试题解析
13. 如图，在 $▱ A B C D$ 中， $∠ O D A = 90 °$ ， $A C = 10$ ， $B D = 6$ ，则 $A D$ 的长为.

查看试题解析
14. 如图，一架 $2.6 m$ 长的梯子AB斜靠在一竖直的墙 $A O$ 上，这时 $A O$ 为 $2.4 m$ ，当梯子的顶端 $A$ 沿墙向下滑的距离 $A C$ 与梯子底端 $B$ 向外移的距离 $B D$ 相等时， $A C$ 的长是m.

查看试题解析
15. 如图，平面直角坐标系中，已知直线 $y = x$ 上一点P（1，1），C为y轴上一点，连接PC，线段PC绕点P顺时针旋转90⁰至线段PD，过点D作直线AB⊥x轴.垂足为B，直线AB与直线 $y = x$ 交于点A，且BD=2AD，连接CD，直线CD与直线 $y = x$ 交于点Q，则点Q的坐标为.

查看试题解析

三、解答题

16. 计算：

(1)、 $(\sqrt{24} - \sqrt{\frac{1}{2}}) - 2 (\sqrt{\frac{1}{8}} - \sqrt{6})$ ；

(2)、 $(3 + \sqrt{5}) (3 - \sqrt{5}) - {(\sqrt{3} - 1)}^{2}$ ；

(3)、 $(\frac{1}{2} \sqrt{28} - \frac{3}{2} \sqrt{84}) \times \sqrt{14}$ ；

(4)、已知 $x = \sqrt{5} - 2$ ，求 $(9 + 4 \sqrt{5}) x^{2} - (\sqrt{5} + 2) x + 4$ 的值.

查看试题解析
17. 如图，在四边形 $A B C D$ 中， $A D ∥ B C$ ， $B D ⊥ A D$ ，点 $E$ ， $F$ 分别是边 $A B$ ， $C D$ 的中点，且 $D E = B F$ .求证：四边形 $A B C D$ 是平行四边形.

查看试题解析
18. 如图，在平面直角坐标系中，O为原点，点A（2，1），B（﹣2，4），直线AB与y轴交于点C ．

(1)、求点C的坐标；

(2)、求证：△OAB是直角三角形．

查看试题解析

19. 随着信息技术的高速发展，计算机技术已是每位学生应该掌握的基本技能.为了提高学生对计算机的兴趣，老师把甲、乙两组各有10名学生，进行电脑汉字输人速度比赛，各组参赛学生每分钟输入汉字个数统计如下表：

输入汉字（个）	132	133	134	135	136	137
甲组人数（人）	1	0	1	5	2	1
乙组人数（人）	0	1	4	1	2	2

(1)、请你填写下表中甲班同学的相关数据.

组别	众数	中位数	平均数（ $\bar{x}$ ）	方差（ $s^{2}$ ）
甲组人数（人）	$a$	$b$	$c$	1.6
乙组人数（人）	134	134.5	135	1.8

则 $a =$ ， $b =$ ， $c =$ ；

(2)、若每分钟输入汉字个数136及以上为优秀，则从优秀人数的角度评价甲、乙两组哪个成绩更好一些？

(3)、请你根据所学的统计知识，从不同角度评价甲、乙两组学生的比赛成绩（至少从两个角度进行评价）

查看试题解析

20. 如图，四边形ABCD是平行四边形，AD=BD，过点C作CE∥BD，交AD的延长线于点E.

(1)、求证：四边形BDEC是菱形；

(2)、连接BE，若AB=2，AD=4，求BE的长.

查看试题解析
21.
“五一”期间，小明一家乘坐高铁前往某市旅游，计划第二天租用新能源汽车自驾出游。
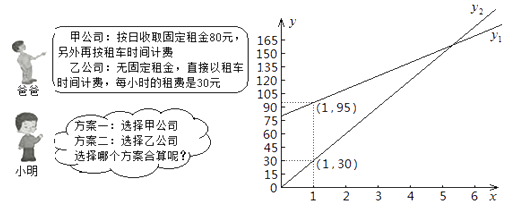
根据以上信息，解答下列问题：

(1)、设租车时间为 $x$ 小时，租用甲公司的车所需费用为 $y_{1}$ 元，租用乙公司的车所需费用为 $y_{2}$ 元，分别求出 $y_{1}$ ， $y_{2}$ 关于 $x$ 的函数表达式；

(2)、请你帮助小明计算并选择哪个出游方案合算。

查看试题解析
22. 如图，四边形 $A B C D$ 为矩形， $A D = 12$ ， $A B > A D$ ，线段 $A B$ 上有一动点 $E$ ，连接 $D E$ ，将 $△ D E A$ 沿 $D E$ 折叠到 $△ D E A^{'}$ .

(1)、如图①，若 $A B = 16$ ，当 $A^{'}$ 落在 $B D$ 上时，求 $A E$ 的长；

(2)、如图②， $G$ 、 $H$ 、 $K$ 分别是线段 $D A$ 、 $D A^{'}$ 、 $E A^{'}$ 的中点，当点 $E$ 在 $A B$ 边上运动时， $∠ G H K$ 的度数是否会发生变化？若不变，求出这个度数；若变化，请说明理由；

(3)、如图③，点 $M$ 、 $N$ ，分别在线段 $D E$ 、 $A D$ 上，连接 $A M$ 、 $M N$ ，当 $∠ A D E = 30 °$ 时，求 $A M + M N$ 的最小值.

查看试题解析
23. 如图，在平面直角坐标系中，直线 $l_{1}$ 交 $x$ 轴于点 $A$ ，交 $y$ 轴于点 $B$ ，点 $B$ 坐标为 $(0 ， 3)$ ，直线 $l_{2} ： y = 2 x$ 与直线 $l_{1}$ 相交于点 $C$ ，点 $C$ 的横坐标为1.

(1)、求直线 $l_{1}$ 的解析式；

(2)、若点 $D$ 是 $y$ 轴上一点，且 $△ O C D$ 的面积是 $△ A O C$ 面积的 $\frac{2}{3}$ ，求点 $D$ 的坐标；

(3)、平面内是否存在一点 $E$ ，使得以点 $O$ ， $A$ ， $C$ ， $E$ 为顶点的四边形是平行四边形？若存在，直接写出符合条件的点 $E$ 的坐标；若不存在，说明理由.

查看试题解析