重庆市渝中区2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2021-07-23 类型：期末考试

进入出卷网下载

一、单选题

1. 下列式子没有意义的是（）

A、 $\sqrt{- 2}$ B、 $\sqrt{0}$ C、 $\sqrt{3}$ D、 $\sqrt{{(- 1)}^{2}}$

查看试题解析
2. 下列函数中，y是x的正比例函数的是（）

A、y＝x² B、y＝ $\frac{1}{x}$ C、y＝ $- \frac{x}{2}$ D、y＝ $\frac{x + 1}{2}$

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{2}$ + $\sqrt{3}$ = $\sqrt{5}$ B、 $\sqrt{8}$ =4 $\sqrt{2}$ C、3 $\sqrt{2}$ ﹣ $\sqrt{2}$ =3 D、 $\sqrt{2}$ $\cdot \sqrt{3}$ = $\sqrt{6}$

查看试题解析
4. 一次函数y＝x﹣1的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 估计 $\sqrt{12} \times \sqrt{\frac{1}{2}}$ 的运算结果应在下列哪两个连续自然数之间（）

A、0和1 B、1和2 C、2和3 D、3和4

查看试题解析
6. 地球的水资源越来越枯竭，全世界都提倡节约用水，小明把自己家1月至6月份的用水量绘制成折线图，那么小明家这6个月的月平均用水量是（　　）

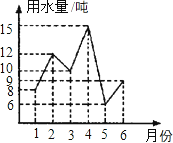A、10吨 B、9吨 C、8吨 D、7吨

查看试题解析
7. 下面哪个特征是矩形、菱形、正方形所共有的（）

A、对角线互相垂直 B、对角线相等 C、对角线互相平分 D、对角线相等且平分

查看试题解析
8. 若数据2、4、x、9、8的平均数是5，则这组数据的中位数是（）

A、2 B、4 C、8 D、9

查看试题解析
9. 如图，一次函数y＝kx+b与y＝﹣x+4的图象相交于点 $P (m ， 1)$ ，则关于x、y的二元一次方程组 ${\begin{array}{l} y = k x + b \\ y = - x + 4 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 3 \\ y = 1 \end{array}$ B、 ${\begin{array}{l} x = 2.6 \\ y = 1 \end{array}$ C、 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ D、 ${\begin{array}{l} x = 1 \\ y = 1 \end{array}$

查看试题解析
10. 《九章算术》中记载“今有竹高一丈，末折抵地，去本三尺.问：折者高几何？”译文：一根竹子，原高一丈，虫伤有病，一阵风将竹子折断，其竹梢恰好着地，着地处离原竹子根部3尺远.问：折断处离地面有多高？（1丈＝10尺）.答：折断处离地面的高度为（）

A、3尺 B、3 $\sqrt{3}$ 尺 C、4尺 D、4.55尺

查看试题解析
11. 如图，矩形ABCD中，动点P从B点出发，沿着B﹣C﹣D﹣A作匀速运动，△ABP的面积y与点P走过的路程x之间的函数图象大致是（）

A、 B、C C、 D、

查看试题解析
12. 如图，在菱形ABCD中，AB＝BD，点E、F分别是AB、AD上任意的点（不与端点重合），且AE＝DF，连接BF与DE相交于点G，连接CG与BD相交于点H.给出如下几个结论：①△AED≌△DFB：②GC平分∠BGD；③S_{四边形BCDG}＝ $\frac{\sqrt{3}}{4}$ CG²；④∠BGE的大小为定值.其中正确的结论个数为（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 计算 $\sqrt{9}$ 的结果是．

查看试题解析
14. 如图，数轴上点A所表示的数是.

查看试题解析
15. 如图，分别过矩形ABCD的顶点A、D作直线l₁、l₂ ，使 $l_{1} // 1_{2}$ ，1₂与边BC交于点P，若 $∠ 1 ＝ 36 °$ ，则∠BPD＝ $°$ .

查看试题解析
16. 甲、乙两名同学的5次射击训练成绩（单位：环）如下表.

比较甲、乙这5次射击成绩的方差S_甲² ， S_乙² ，结果为：S_甲²S_乙².（选填“＞”“＝”或“＜”）

查看试题解析
17. 如图所示，在矩形ABCD中，AB＝6，AD＝8，P是AD上的动点，PE⊥AC，PF⊥BD于F，则PE+PF的值为.

查看试题解析
18. 武汉疫情爆发期间，大学生小玲和小丽应聘成为了阳光小区的疫情防控志愿者.一天早晨，小玲从阳光小区出发骑三轮车匀速到距离7500米处的区疾病防控中心领取防疫物资，出发一段时间后，小丽发现小玲忘记带了社区介绍信，立即骑自行车沿小玲行驶的路线匀速行驶去追赶，当小丽追上小玲后，立即将介绍信交给了她，并用2分钟时间与小玲核对了一下防疫物资的清单，然后小玲继续以原速度前往区疾病防控中心，而小丽则按原路以原来速度的一半匀速返回阳光小区.设小丽与小玲之间的距离y（米）与小玲从阳光小区出发后的时间x（分）之间的关系如图所示.当小丽刚好返回到阳光小区时，小玲离区疾病防控中心的距离还有米.

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{12} + | 1 - \sqrt{3} | - {(π - 3)}^{0}$ ；

(2)、 $(\sqrt{18} + 2) \div \sqrt{2} - {(\sqrt{2} - 1)}^{2}$ .

查看试题解析
20. 为宣传防护知识，增强免疫能力，某班举行了“防疫”知识测试，测试共10道题，以下是根据测试结果绘制的不完整的扇形统计图和条形统计图，请根据相关信息，解答下列问题：

(1)、图1中m的值为；

(2)、补全条形统计图；

(3)、求该班学生答对题数的平均数、众数和中位数.

查看试题解析
21. 如图， $▱ A B C D$ 中，E、F是对角线BD上的两个点，且DF $=$ BE.求证： $A E // C F$ .

查看试题解析
22. 如图，已知△ABC中，AB＝AC，BC＝5，D为AB上一点，CD＝4，BD＝3.

(1)、求证： $∠ B D C ＝ 90 °$ ；

(2)、求AC的长.

查看试题解析
23. 如图，直线 $y = 2 x - 2$ 与x轴、y轴分别相交于点A、点B.

(1)、求点A、点B的坐标.

(2)、将直线AB向上平移3个单位得直线l，若C为直线l上一点，且S_△AOC＝3，求点C的坐标.

查看试题解析
24. 数形结合是一种重要的数学思想方法，我们可以借助函数的图象求某些较为复杂不等式的解集.比如，求不等式 $x - 1 > \frac{2}{x}$ 的解集，可以先构造两个函数 $y_{1} = x - 1$ 和 $y_{2} = \frac{2}{x}$ ，再在同一平面直角坐标系中画出这两个函数的图象（如图1所示），通过观察所画函数的图象可知：它们交于 $A (- 1 ， - 2)$ 、 $B (2 ， 1)$ 两点，当 $- 1 < x < 0$ 或 $x > 2$ 时，y₁＞y₂ ，由此得到不等式 $x - 1 > \frac{2}{x}$ 的解集为 $- 1 < x < 0$ 或x＞2.

根据上述说明，解答下列问题：

(1)、要求不等式x²＋3x＞x＋3的解集，可先构造出函数y₁＝x²＋3x和函数y₂＝；

(2)、图2中已作出了函数y₁＝x²＋3x的图象，请在其中作出函数y₂的图象；

(3)、观察所作函数的图象，求出不等式x²＋3x＞x＋3的解集.

查看试题解析
25. 如图，在正方形ABCD中，E为CD边上一点，以DE为边向外作正方形DEFG，将正方形DEFG绕点D顺时针旋转，连接AG.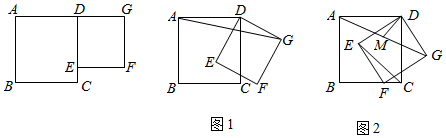

(1)、如图1，若AD＝2 $\sqrt{3}$ 、DE＝2，当 $∠ A D G ＝ 150 °$ 时，求AG的长；

(2)、如图2，正方形DEFG绕点D旋转的过程中，取AG的中点M，连接DM、CE，猜想：DM和CE之间有何等量关系？并利用图2加以证明.

查看试题解析
26. 如图，平面直角坐标系中，已知点C的坐标为 $(\sqrt{3} ， - 2)$ ，直线AB与x轴、y轴分别交于点A、点B，且点B的坐标为 $(0 ， 3)$ ， $∠ B A O ＝ 30 °$ .

(1)、求直线AB的解析式；

(2)、若点D、E分别是y轴和直线AB上的动点，当CD+DE取得最小值时，是否存在点P使得以P、C、D、E为顶点的四边形是平行四边形？如果存在，请求出点P的坐标；如果不存在，请说明理由.

查看试题解析