浙江省临海市2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2021-07-23 类型：期末考试

进入出卷网下载

一、单选题

1. 若函数 $y = k x$ 的图象经过第一、三象限，则 $k$ 的值可以为（）

A、 $- 2$ B、 $- \frac{1}{2}$ C、0 D、2

查看试题解析
2. 下列各式中，属于最简二次根式的是（）

A、 $\sqrt{4}$ B、 $\sqrt{\frac{1}{3}}$ C、 $\sqrt{2}$ D、 $\sqrt{8}$

查看试题解析
3. 某文具店上个月某款书包各种颜色的销售记录如下表，该店决定多进一些蓝色书包，依据的统计量是（）

书包颜色

红

蓝

紫

白

黑

销量（个）

56

87

67

68

50

A、平均数 B、众数 C、中位数 D、方差

查看试题解析
4. 下列运算错误的是（）

A、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ B、 $\sqrt{8} \div \sqrt{4} = \sqrt{2}$ C、 ${(\sqrt{5})}^{2} = 5$ D、 $2 \div \sqrt{5} = 2 \sqrt{5}$

查看试题解析
5. 如图，每个小正方形的边长为1，四边形的顶点 $A ， B ， C ， D$ 都在格点上，则下面4条线段长度为 $\sqrt{10}$ 的是（）

A、 $A B$ B、 $B C$ C、 $C D$ D、 $A D$

查看试题解析
6. 如图，菱形 $A B C D$ 的对角线 $A C$ ， $B D$ 相交于点 $O$ ， $E$ 是 $A B$ 的中点， $O E = 2$ ，则菱形 $A B C D$ 的周长为（）

A、8 B、 $8 \sqrt{3}$ C、16 D、20

查看试题解析
7. 对于一次函数 $y = 2 x - 1$ ，当自变量 $x$ 的值增加1时，函数值将（）

A、增加2 B、增加1 C、减少2 D、减少1

查看试题解析
8. 如图， $▱ A B C D$ 中的对角线 $A C$ ， $B D$ 相交于点 $O$ ，点 $E ， F$ 在 $B D$ 上，且 $B E = D F$ ，连接 $A E$ ， $E C$ ， $C F$ ， $F A$ ，下列条件能判定四边形 $A E C F$ 为矩形的是（）

A、 $B E = E O$ B、 $E O = \frac{1}{2} A C$ C、 $A C ⊥ B D$ D、 $A E = A F$

查看试题解析
9. 甲、乙两人进行1500米比赛，在比赛过程中，两人所跑的路程 $y$ （米）与所用的时间 $x$ （分）的函数关系如图所示，则下列说法正确的是（）

A、甲先到达终点 B、跑到2分钟时，两人相距200米 C、甲的速度随时间的增大而增大 D、起跑2分钟后，甲的速度大于乙的速度

查看试题解析
10. 如图，在 $R t Δ A B C$ 中， $∠ B A C = 90 °$ ， $D$ 是 $B C$ 中点，分别以 $A B$ ， $A C$ 为边向外作正方形 $A B E F$ 和正方形 $A C G H$ ，连接 $F D$ ， $H D$ .若 $B C = 6$ ，则阴影部分的面积是（）

A、 $6 \sqrt{2}$ B、12 C、9 D、6

查看试题解析

二、填空题

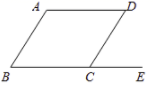
11. 若式子 $\sqrt{a - 1}$ 在实数范围内有意义，则 $a$ 的取值范围是.

查看试题解析
12. 在Rt $△$ ABC中，∠C=90^o ， AC=6，BC=8，则AB边的长是.

查看试题解析
13. 如图，点E在 $▱ A B C D$ 的边 $B C$ 的延长线上，若 $∠ D C E = 60 °$ ，则 $∠ A =$ $°$ ．

查看试题解析
14. 将直线 $y = x + 2$ 向下平移3个单位，得到的直线解析式是.

查看试题解析

15. 在一次中学生田径运动会上，参加男子跳高的15名运动员成绩如下表

成绩（米）	1.50	1.60	1.65	1.70	1.75	1.80
人数（个）	2	3	3	2	4	1

则这些运动员成绩的中位数是米.

查看试题解析

16. 如图，把图1中边长分别为3和4的两个全等矩形沿对角线分成四个全等的直角三角形，将这四个全等的直角三角形拼成图2所示的正方形，则图2中阴影部分的面积为.

查看试题解析
17. 若一次函数 $y = k x + b$ 的图象经过点 $(1 ， - 1)$ ， $(2 ， 1)$ ，则不等式 $k x + b > 1$ 的解集为.

查看试题解析
18. 公元3世纪，我国数学家刘徽就能利用近似公式 $\sqrt{a^{2} + r} \approx a + \frac{r}{2 a}$ 得到根式的近似值.利用此公式就可以估计 $\sqrt{10}$ 的近似值， $\sqrt{10} = \sqrt{3^{2} + 1}$ $\approx$ （精确到0.01）.

查看试题解析
19. 如图， $∠ C A B = 30 °$ ，点 $D$ 在射线 $A B$ 上，且 $A D = 4$ ，点 $P$ 在射线 $A C$ 上运动，当 $Δ A D P$ 是直角三角形时， $P D$ 的长为.

查看试题解析
20. 如图是利用矩形纸片折纸飞机的前三步操作（阴影部分为重叠部分），在进行第2次折叠时，发现两条折痕刚好经过矩形纸片的两个顶点，则 $\frac{A B}{A D} =$ .

查看试题解析

三、解答题

21. 计算：

(1)、 $\sqrt{12} - \sqrt{3}$ ；

(2)、 $\sqrt{2} (\sqrt{8} + \sqrt{\frac{1}{2}})$ .

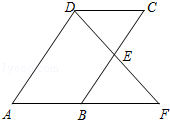
查看试题解析
22. 如图，在平行四边形ABCD中，E为BC的中点，连接DE.延长DE交AB的延长线于点F.求证：AB=BF.

查看试题解析

23. 为从甲、乙两名学生中选拔一名参加“疫情防控知识竞赛”，老师组织了5次模拟测试，下面是这五次成绩的统计表、统计图及部分统计量的计算信息.

甲、乙两位同学5次成绩统计表

	第1次	第2次	第3次	第4次	第5次
甲同学	75	90	95	80	85
乙同学	80	90	80	85	90

乙同学的平均数和方差：

$\bar{x} = \frac{80 + 90 + 80 + 85 + 90}{5} = 85$

$S_{乙}^{2} = \frac{{(80 - 85)}^{2} + {(90 - 85)}^{2} + \dots + {(90 - 85)}^{2}}{5} = 20$

(1)、补充完整折线统计图；

(2)、求甲同学成绩的方差；

(3)、请你根据已学的统计知识，判断谁更适合参加竞赛？并说明理由.

查看试题解析

24. 我国是世界上水资源最缺乏的国家之一，同时又有很多水龙头由于漏水造成大量的浪费.某校园内有一个漏水的水龙头，数学活动小组用最大容量为200毫升的量筒接水，每隔10秒钟观察量筒中水的体积，从某一时刻起记录1分钟内量筒中水的体积如下表（精确到 $1 m l$ ）：

时间 $t (s)$

10

20

30

40

50

60

量筒中的水量 $V (m l)$

30

45

60

75

90

105

(1)、在平面直角坐标系中描出表中数据对应的点；

(2)、量筒中的水量 $V (m l)$ 是否为时间 $t (s)$ 的函数？如果是，试求出一个符合表中数据的函数解析式；

(3)、若水费为3.6元/ $m^{3}$ ，按这样的漏水速度，这个水龙头一个月（30天）要浪费多少钱？（ $1 m^{3} = 10^{6} m l$ ，结果保留整数）.

查看试题解析
25. 已知一次函数 $y_{1} = k x + b$ ，图象经过点 $(1 ， 2)$

(1)、请直接写出 $k ， b$ 满足的关系式；

(2)、若 $- 1 \leq x \leq 4$ 时， $y_{1}$ 有最大值3，求 $k$ 的值；

(3)、若有函数 $y_{2} = (a - 2) x + 2 a (a \neq 2)$ ，对于任意实数 $x$ ，都有 $y_{1} < y_{2}$ 成立，求 $k$ 与 $a$ 的数量关系及 $a$ 的取值范围.

查看试题解析
26. 如图，在矩形 $A B C D$ 中， $A B = a$ ， $B C = b$ ，点 $F$ 在 $D C$ 的延长线上，点 $E$ 在 $A D$ 上，且有 $∠ C B E = \frac{1}{2} ∠ A B F$ .

(1)、如图1，当 $a = b$ 时，若 $∠ C B E = 60 °$ ，求证： $B E = B F$ ；

(2)、如图2，当 $b = \frac{3}{2} a$ 时，
①请直接写出 $∠ A B E$ 与 $∠ B F C$ 的数量关系： ▲ ；

②当点 $E$ 是 $A D$ 中点时，求证： $C F + B F = 2 a$ ；

③在②的条件下，请直接写出 $S_{Δ B C F} ： S_{矩形 A B C D}$ 的值.

查看试题解析

时间 $t (s)$	10	20	30	40	50	60
量筒中的水量 $V (m l)$	30	45	60	75	90	105

书包颜色	红	蓝	紫	白	黑
销量（个）	56	87	67	68	50