宁夏回族自治区石嘴山市平罗县2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2021-07-23 类型：期末考试

进入出卷网下载

一、单选题

1. 若 $\sqrt{x - 2}$ 在实数范围内有意义，则x的取值范围（　　）

A、x≥2 B、x≤2 C、x＞2 D、x＜2

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{3} + \sqrt{3} = \sqrt{6}$ B、 $\sqrt{3} + \sqrt{3} = 2 \sqrt{3}$ C、 $\sqrt{3} \times \sqrt{3} = \sqrt{6}$ D、 $\sqrt{3} + \sqrt{3} = 3 \sqrt{3}$

查看试题解析
3. 如图，将一张矩形纸片折叠，若∠1＝78°，则∠2的度数是（）

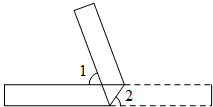A、51° B、56° C、61° D、78°

查看试题解析
4. 下列结论中，矩形具有而菱形不一定具有的性质是（）

A、内角和为360° B、对角线互相平分 C、对角线相等 D、对角线互相垂直

查看试题解析
5. 已知一次函数y＝kx+2，若y随x的增大而减小，则它的图象经过（）

A、第一、二、三象限 B、第一、二、四象限 C、第一、三、四象限 D、第二、三、四象限

查看试题解析
6. 如图，Rt△ABC中，∠ACB＝90°，若AB＝15cm，则正方形ADEC和正方形BCFG的面积之和为（）

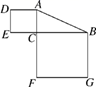A、150cm² B、200cm² C、225cm² D、无法计算

查看试题解析
7. 某班50人一周内在线学习数学的时间如图所示，则以下叙述正确的是（）

A、全班同学在线学习数学的平均时间为2.5h B、全班同学在线学习数学时间的中位数是2h C、全班同学在线学习数学时间的众数是20h D、全班超过半数学生每周在线学习数学的时间超过3h

查看试题解析
8. 如图，一次函数y＝kx+b的图象经过点A（1，0），B（2，1），当因变量y＞0时，自变量x的取值范围是（　　）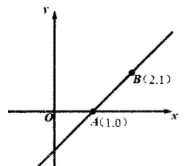

A、x＞0 B、x＜0 C、x＞1 D、x＜1

查看试题解析

二、填空题

9. 计算： $2^{- 1} + \sqrt{4}$ = ．

查看试题解析
10. 若点（m，m+3）在函数y=﹣x+2的图象上，则m=.

查看试题解析
11. 射击训练中，甲、乙、丙、丁四人每人射击10次，平均环数均为8.7环，方差分别为 $S_{甲}^{2} = 0.51$ ， $S_{乙}^{2} = 0.41$ ， $S_{丙}^{2} = 0.62$ ， $S_{丁}^{2} = 0.45$ ，则四人中成绩最稳定的是．

查看试题解析
12. 如图，菱形ABCD中，对角线AC、BD相交于点O，H为AD边中点，菱形ABCD的周长为16，则OH的长等于.

查看试题解析
13. 将直线y=2x-1向上平移动4个单位长度后，所得直线的解析式为

查看试题解析
14. 如图，每个小正方形的边长都为1，则 $Δ A B C$ 的三边长 $a$ ， $b$ ， $c$ 的大小关系是（用“>”连接）.

查看试题解析
15. 某公司招聘员工一名，某应聘者进行了三项素质测试，其中创新能力为70分，综合知识为80分，语言表达为90分，如果将这三项成绩按5：3：2计入总成绩，则他的总成绩为分.

查看试题解析
16. 如图，下列条件之一能使平行四边形ABCD是菱形的为.
①AC⊥BD；②∠BAD=90°；③AB=BC；④AC=BD.

查看试题解析
17. 如图， $▱ A B C D$ 中， $A D = 2 A B$ ， $A H ⊥ C D$ 于点 $H$ ， $N$ 为 $B C$ 中点，若 $∠ D = 68 °$ ，则 $∠ N A H =$ $°$ .

查看试题解析

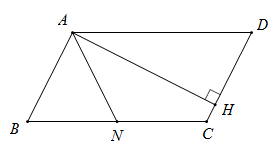
三、解答题

18. 计算： $\sqrt{27} - \sqrt{2} \times \sqrt{6} - \sqrt{18}$ .

查看试题解析
19. 设 $a = - 1 + \sqrt{3}$ ， $b = - 1 - \sqrt{3}$ ，求 $a + b$ ，ab的值.

查看试题解析
20. 一艘轮船以16千米/时的速度离开港口向正北方向航行，另一艘轮船同时离开港口以12千米/时的速度向正东方向航行，它们离开港口半小时后相距多少千米?

查看试题解析
21. 如图，在Rt△ABC中，∠C=90°，点D是AC上一点，∠BDC=45°，AB=13，BC=5.

(1)、求BD的长；

(2)、求AD的长.

查看试题解析
22. 如图，已知四边形ABCD是平行四边形，点E、B、D、F在同一直线上，且BE=DF．求证：AE=CF．

查看试题解析
23. 已知，如图，在Rt△ABC中，∠ACB＝90°，D、E分别是AB、AC的中点，F是BC延长线上的一点，且EF∥DC，

(1)、求证：四边形CDEF是平行四边形；

(2)、若EF＝2cm，求AB的长.

查看试题解析
24. 某校为了解初中学生每天在校体育活动的时间（单位：h），随机调查了该校的部分初中学生．根据调查结果，绘制出如下的统计图①和图②．请根据相关信息，解答下列问题：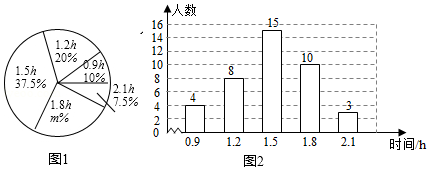

(1)、本次接受调查的初中学生人数为，图①中m的值为；

(2)、求统计的这组每天在校体育活动时间数据的平均数、众数和中位数；

(3)、根据统计的这组每天在校体育活动时间的样本数据，若该校共有800名初中学生，估计该校每天在校体育活动时间大于1h的学生人数．

查看试题解析
25. 如图，直线y=kx+b经过点A（-5，0），B（-1，4）

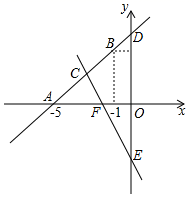(1)、求直线AB的表达式；

(2)、求直线CE：y=-2x-4与直线AB及y轴围成图形的面积；

(3)、根据图象，直接写出关于x的不等式kx+b＞-2x-4的解集.

查看试题解析
26. 一家蔬菜公司计划到某绿色蔬菜基地收购A，B两种蔬菜共140吨，预计两种蔬菜销售后获利的情况如表所示：

销售品种

A种蔬菜

B种蔬菜

每吨获利（元）

1200

1000

其中A种蔬菜的5%、B种蔬菜的3%须运往C市场销售，但C市场的销售总量不超过5.8吨．设销售利润为W元（不计损耗），购进A种蔬菜x吨．

(1)、求W与x之间的函数关系式；

(2)、将这140吨蔬菜全部销售完，最多可获得多少利润？

查看试题解析

销售品种	A种蔬菜	B种蔬菜
每吨获利（元）	1200	1000