湖南省株洲市渌口区2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2021-07-23 类型:期末考试
一、单选题
-
1. 下列图形是我国国产品牌汽车的标识,在这些汽车标识中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 勾股定理是“人类最伟大的十个科学发现之一”.我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的,他用来证明勾股定理的图案被称为“赵爽弦图”.2002年在北京召开的国际数学大会选它作为会徽.下列图案中是“赵爽弦图”的是( )A、
2. 勾股定理是“人类最伟大的十个科学发现之一”.我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的,他用来证明勾股定理的图案被称为“赵爽弦图”.2002年在北京召开的国际数学大会选它作为会徽.下列图案中是“赵爽弦图”的是( )A、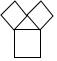 B、
B、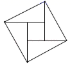 C、
C、 D、
D、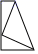 3. 下列说法中不正确的是( )A、四边相等的四边形是菱形 B、对角线垂直的平行四边形是菱形 C、菱形的对角线互相垂直且相等 D、菱形的邻边相等4. 如图,D是△ABC内一点,BD⊥CD,AD=7,BD=4,CD=3,E,F,G,H分别是AB,BD,CD,AC的中点,则四边形EFGH的周长为( )
3. 下列说法中不正确的是( )A、四边相等的四边形是菱形 B、对角线垂直的平行四边形是菱形 C、菱形的对角线互相垂直且相等 D、菱形的邻边相等4. 如图,D是△ABC内一点,BD⊥CD,AD=7,BD=4,CD=3,E,F,G,H分别是AB,BD,CD,AC的中点,则四边形EFGH的周长为( )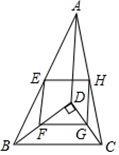 A、12 B、14 C、24 D、215. 如图,在正方形 的外侧,作等边 ,则 为( )
A、12 B、14 C、24 D、215. 如图,在正方形 的外侧,作等边 ,则 为( )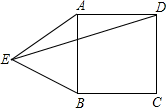 A、15° B、35° C、45° D、55°6. 在平面直角坐标系中,点P(-2,x2+1)所在的象限是( )
A、15° B、35° C、45° D、55°6. 在平面直角坐标系中,点P(-2,x2+1)所在的象限是( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 在平面直角坐标系中,点A(m,2)与点B(3,n)关于y轴对称,则( )A、m=3,n=2 B、m=﹣3,n=2 C、m=2,n=3 D、m=﹣2,n=﹣38. 在函数 中,自变量 的取值范围是( )A、 B、 C、 且 D、 且9. 若b>0,则一次函数y=﹣x+b的图象大致是( )A、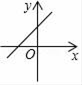 B、
B、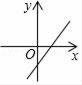 C、
C、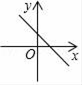 D、
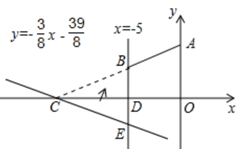
D、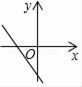 10. 如图,直角坐标系xOy中,A(0,5),直线x=﹣5与x轴交于点D,直线y=﹣ x﹣ 与x轴及直线x=﹣5分别交于点C,E,点B,E关于x轴对称,连接AB.
10. 如图,直角坐标系xOy中,A(0,5),直线x=﹣5与x轴交于点D,直线y=﹣ x﹣ 与x轴及直线x=﹣5分别交于点C,E,点B,E关于x轴对称,连接AB.①C(﹣13,0),E(﹣5,﹣3);
②直线AB的解析式为:y= x+5;
③设面积的和S=S△CDE+S四边形ABDO , 则S=32;
④在求面积的和S=S△CDE+S四边形ABDO时,琪琪有个想法:“将△CDE沿x轴翻折到△CDB的位置,而△CDB与四边形ABDO拼接后可看成△AOC,即S=S△CDE+S四边形ABDO=S△AOC”.
其中正确的结论个数是( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
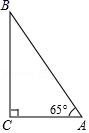
11. 如图示在△ABC中∠B= .
 12. 如图,△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于点D.若∠A=30°,AE=6cm,则BC= .
12. 如图,△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于点D.若∠A=30°,AE=6cm,则BC= .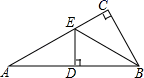 13. 一组数据4, , ,4, ,4, ,4中,出现次数最多的数是4,其频率是.14. 在平行四边形ABCD中,AB=8,BC=10,∠B=30°,则▱ABCD的面积为.15. 将直线y=3x+1向下平移5个单位得到的直线的表达式是 .16. 已知一次函数y=kx+4(k<0)的图象与两坐标轴所围成的三角形的面积等于8,则k的值为 .17. 如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠OAE=15°,则∠ADB的度数为.
13. 一组数据4, , ,4, ,4, ,4中,出现次数最多的数是4,其频率是.14. 在平行四边形ABCD中,AB=8,BC=10,∠B=30°,则▱ABCD的面积为.15. 将直线y=3x+1向下平移5个单位得到的直线的表达式是 .16. 已知一次函数y=kx+4(k<0)的图象与两坐标轴所围成的三角形的面积等于8,则k的值为 .17. 如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠OAE=15°,则∠ADB的度数为.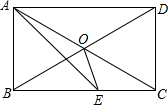 18. 如图,在Rt△ABC中,∠BAC=90°,∠ABC的平分线交AC于D.过点A作AE⊥BC于E,交BD于G,过点D作DF⊥BC于F,过点G作GH∥BC,交AC于点H,则下列结论:①∠BAE=∠C;②S△ABG:S△EBG=AB:BE;③∠ADF=2∠CDF;④四边形AGFD是菱形;⑤CH=DF.其中正确的结论是.
18. 如图,在Rt△ABC中,∠BAC=90°,∠ABC的平分线交AC于D.过点A作AE⊥BC于E,交BD于G,过点D作DF⊥BC于F,过点G作GH∥BC,交AC于点H,则下列结论:①∠BAE=∠C;②S△ABG:S△EBG=AB:BE;③∠ADF=2∠CDF;④四边形AGFD是菱形;⑤CH=DF.其中正确的结论是.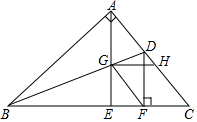
三、解答题
-
19. 已知y是x的一次函数,当 时, ;当 时, ,求:(1)、这个一次函数的表达式和自变量x的取值范围(2)、当 时,自变量x的值(3)、当 时,自变量x的取值范围.20. 点P是平面直角坐标系中的一点且不在坐标轴上,过点P向x轴、y轴作垂线段,若垂线段的长度的和为4,则点P叫做“垂距点”,例如:如图中的点P(1,3)是“垂距点”.
 (1)、在点A(﹣2,2), ,C(﹣1,5)是“垂距点”是;(2)、若 是“垂距点”,求m的值.21. 2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注,某市一研究机构为了了解 岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了如下尚不完整的频数分布表、频数分布走访图和扇形统计图:
(1)、在点A(﹣2,2), ,C(﹣1,5)是“垂距点”是;(2)、若 是“垂距点”,求m的值.21. 2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注,某市一研究机构为了了解 岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了如下尚不完整的频数分布表、频数分布走访图和扇形统计图:组别
年龄段
频数(人数)
第1组
5
第2组
第3组
35
第4组
20
第5组
15
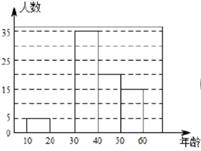
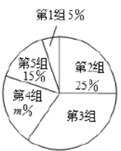 (1)、请直接写出 、 的值及扇形统计图中第3组所对应的圆心角的度数;(2)、请补全上面的频数分布直方图;(3)、假设该市现有 岁的市民300万人,问第4组年龄段关注本次大会的人数经销商有多少万人?22. 如图, , 分别是 的高,且 ,求证: .
(1)、请直接写出 、 的值及扇形统计图中第3组所对应的圆心角的度数;(2)、请补全上面的频数分布直方图;(3)、假设该市现有 岁的市民300万人,问第4组年龄段关注本次大会的人数经销商有多少万人?22. 如图, , 分别是 的高,且 ,求证: .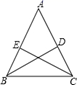 23. 如图,四边形ABCD是平行四边形,延长CB至点E,使得BE=BC,连结DE交AB于点F.
23. 如图,四边形ABCD是平行四边形,延长CB至点E,使得BE=BC,连结DE交AB于点F.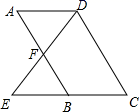 (1)、求证:△ADF≌△BEF.(2)、连结DB,若AD=DB=5,CD=6,求DE的长.24. 如图,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.
(1)、求证:△ADF≌△BEF.(2)、连结DB,若AD=DB=5,CD=6,求DE的长.24. 如图,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.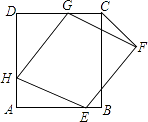 (1)、求证:∠HEA=∠CGF;(2)、当AH=DG时,求证:菱形EFGH为正方形.25. 某种动物的身高y(dm)是其腿长x(dm)的一次函数.当动物的腿长为6dm时,身高为45.5dm;当动物的腿长为14dm时,身高为105.5dm .(1)、写出y与x之间的关系式;(2)、当该动物腿长10dm时,其身高为多少?26. 如图所示,在平面直角坐标系中,过点A(﹣ ,0)的两条直线分别交y轴于B,C两点,∠ABO=30°,OB=3OC.
(1)、求证:∠HEA=∠CGF;(2)、当AH=DG时,求证:菱形EFGH为正方形.25. 某种动物的身高y(dm)是其腿长x(dm)的一次函数.当动物的腿长为6dm时,身高为45.5dm;当动物的腿长为14dm时,身高为105.5dm .(1)、写出y与x之间的关系式;(2)、当该动物腿长10dm时,其身高为多少?26. 如图所示,在平面直角坐标系中,过点A(﹣ ,0)的两条直线分别交y轴于B,C两点,∠ABO=30°,OB=3OC.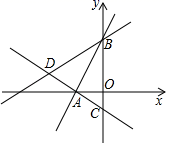 (1)、证明:AC⊥AB;(2)、将 ABC沿直线AB翻折得到 ABD,求直线BD的函数解析式;(3)、在(2)的条件下,设直线BD交x轴于点E,嘉淇认为 ADE的面积与 AOB的面积相同,请判断嘉淇的观点是否正确.
(1)、证明:AC⊥AB;(2)、将 ABC沿直线AB翻折得到 ABD,求直线BD的函数解析式;(3)、在(2)的条件下,设直线BD交x轴于点E,嘉淇认为 ADE的面积与 AOB的面积相同,请判断嘉淇的观点是否正确.