湖南省长沙市天心区长郡教育集团2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2021-07-23 类型：期末考试

进入出卷网下载

一、单选题

1. 下列函数关系式：①y＝－2x；②y＝ $\frac{2}{x}$ ；③y＝－2 $x^{2}$ ；④y＝2；⑤y＝2x－1.其中是一次函数的是（）

A、①⑤ B、①④⑤ C、②⑤ D、②④⑤

查看试题解析
2. 若一次函数 $y = (a - 3) x - a$ 的图象经过第二、三、四象限，则a的取值范围是（）

A、a≠3 B、a＞0 C、a＜3 D、0＜a＜3

查看试题解析
3. 如下图，▱ABCD中，∠A比∠D大40°，则∠C等于（）

A、70° B、100° C、110° D、120°

查看试题解析
4. 如图，在 $▱$ ABCD中，点E，F分别在边BC，AD上，有下列条件：①BE=DF；②AE∥CF；③AE=CF；④∠BAE=∠DCF．其中，能使四边形AECF是平行四边形的条件有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 据了解，某定点医院收治的7名新型冠状肺炎患者的新冠病毒潜伏期分别为2天，3天，3天，4天，4天，4天，7天，则这7名患者新冠病毒潜伏期的众数和中位数分别为（）

A、4天，4天 B、3天，4天 C、4天，3天 D、3天，7天

查看试题解析
6. 甲、乙、丙、丁四名射击运动员参加射击预选赛，他们射击成绩的平均环数 $\bar{x}$ 及方差S²如表所示，

甲

乙

丙

丁

$\bar{x}$

8

9

9

8

S²

1

1.1

1.2

1.3

若要选出一个成绩较好且状态稳定的运动员去参赛，那么应选运动员（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
7. 若方程（m﹣1） $x^{m^{2} + 1}$ ﹣x﹣2＝0是一元二次方程，则m的值为（）

A、0 B、±1 C、1 D、﹣1

查看试题解析
8. 用配方法解方程x²+2x﹣1＝0时，配方结果正确的是（）

A、（x+2）²＝2 B、（x+1）²＝2 C、（x+2）²＝3 D、（x+1）²＝3

查看试题解析
9. 把抛物线y＝x²向上平移3个单位，再向右平移1个单位，则平移后抛物线的解析式为（　　）

A、y＝（x+3）²+1 B、y＝（x+3）²﹣1 C、y＝（x﹣1）²+3 D、y＝（x+1）²+3

查看试题解析
10. 如图，矩形纸片ABCD中，点E、F分别在线段BC、AB上，将△BEF沿EF翻折，点B落在AD上的点P处，且AB＝4，BE＝5，则AP的长为（）

A、1 B、2 C、3 D、4

查看试题解析
11. 二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，则下列结论正确的是（）

A、 $a b c > 0$ B、 $a + b + c = 0$ C、 $4 a - 2 b + c < 0$ D、 $b^{2} - 4 a c < 0$

查看试题解析
12. 已知二次函数y＝﹣x²+2x+3，截取该函数图象在0≤x≤4间的部分记为图象G，设经过点（0，t）且平行于x轴的直线为l，将图象G在直线l下方的部分沿直线l翻折，图象G在直线上方的部分不变，得到一个新函数的图象M，若函数M的最大值与最小值的差不大于5，则t的取值范围是（）

A、﹣1≤t≤0 B、﹣1≤t $\leq - \frac{1}{2}$ C、 $- \frac{1}{2} \leq t \leq 0$ D、t≤﹣1或t≥0

查看试题解析

二、填空题

13. 计算5个数据的方差时，得s²＝ $\frac{1}{5}$ [（5﹣ $\bar{x}$ ）²+（8﹣ $\bar{x}$ ）²+（7﹣ $\bar{x}$ ）²+（4﹣ $\bar{x}$ ）²+（6﹣ $\bar{x}$ ）²]，则 $\bar{x}$ 的值为．

查看试题解析
14. 已知一次函数 $y = - 3 x + m$ 的图形经过了A（x₁ ， 1），B（x₂ ， -2），C（x₃ ， 3），则x₁ ， x₂ ， x₃的大小关系为.

查看试题解析
15. 一抛物线和另一抛物线y＝﹣2x²的形状和开口方向完全相同，且顶点坐标是（﹣2，1），则该抛物线的解析式为.

查看试题解析
16. 已知关于 $x$ 的方程 $a x^{2} + 2 x - 3 = 0$ 有两个不相等的实数根，则 $a$ 的取值范围是．

查看试题解析
17. 如图，菱形ABCD中，对角线AC与BD相交于点O，且AC=24，BD=10，则菱形ABCD的高DE=.

查看试题解析
18. 如图，在Rt△ABC中，∠BAC=90°，AB=5，AC=12，P为边BC上一动点（P不与B、C重合），PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的取值范围是.

查看试题解析

三、解答题

19. 如图，直线AB与x轴交于点A（1，0），与y轴交于点B（0，﹣2）．

(1)、求直线AB的解析式；

(2)、若直线AB上的点C在第一象限，且S_△_BOC=2，求点C的坐标．

查看试题解析
20. 如图，已知菱形ABCD的对角线相交于点O，延长AB至点E，使BE=AB，连接CE．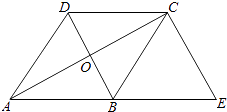

(1)、求证：BD=EC；

(2)、若∠E=50°，求∠BAO的大小．

查看试题解析
21. 某校在开展读书交流活动中全体师生积极捐书．为了解所捐书籍的种类，对部分书籍进行了抽样调查，李老师根据调查数据绘制了如图所示不完整统计图．请根据统计图回答下面问题：

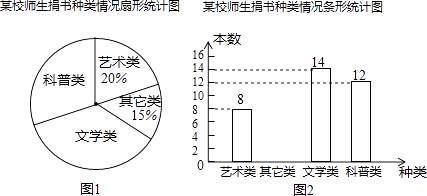(1)、本次抽样调查的书籍有多少本？请补全条形统计图；

(2)、求出图1中表示文学类书籍的扇形圆心角度数；

(3)、本次活动师生共捐书1200本，请估计有多少本科普类书籍？

查看试题解析
22. 如图，已知抛物线y= $- x^{2}$ +mx+3与x轴交于A，B两点，与y轴交于点C，点B的坐标为（3，0），

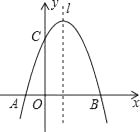(1)、求m的值及抛物线的顶点坐标．

(2)、点P是抛物线对称轴l上的一个动点，当PA+PC的值最小时，求点P的坐标．

查看试题解析
23. 甲商品的进价为每件20元，商场确定其售价为每件40元．

(1)、若现在需进行降价促销活动，预备从原来的每件40元进行两次调价，已知该商品现价为每件32.4元．若该商品两次调价的降价率相同，求这个降价率；

(2)、经调查，该商品每降价0.2元，即可多销售10件．已知甲商品售价40元时每月可销售500件，若该商场希望该商品每月能盈利10000元，且尽可能扩大销售量，则该商品在原售价的基础上应如何调整？

查看试题解析
24. “扬州漆器”名扬天下，某网店专门销售某种品牌的漆器笔筒，成本为30元/件，每天销售量 $y$ （件）与销售单价 $x$ （元）之间存在一次函数关系，如图所示.

(1)、求 $y$ 与 $x$ 之间的函数关系式；

(2)、如果规定每天漆器笔筒的销售量不低于240件，当销售单价为多少元时，每天获取的利润最大，最大利润是多少？

(3)、该网店店主热心公益事业，决定从每天的销售利润中捐出150元给希望工程，为了保证捐款后每天剩余利润不低于3600元，试确定该漆器笔筒销售单价的范围.

查看试题解析
25. 在正方形ABCD中，E是△ABD内的点，EB=EC.

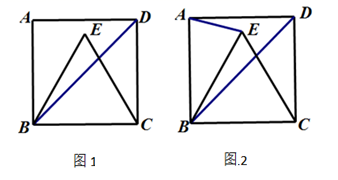(1)、如图1，若EB=BC，求∠EBD的度数；

(2)、如图2，EC与BD交于点F，连接AE，若 $S_{四边形 A B F E} = a$ ，试探究线段FC与BE之间的等量关系，并说明理由.

查看试题解析
26. 已知函数y₁＝x，y₂＝x²+bx+c，α，β为方程y₁﹣y₂＝0的两个根，点M（t，T）在函数y₂的图象上.

(1)、若α＝ $\frac{1}{3}$ ，β＝ $\frac{1}{2}$ ，求函数y₂的解析式；

(2)、在（1）的条件下，若函数y₁与y₂的图象的两个交点为A，B，当△ABM的面积为 $\frac{1}{12^{3}}$ 时，求t的值；

(3)、若0＜α＜β＜1，当0＜t＜1时，试确定T，α，β三者之间的大小关系，并说明理由.

查看试题解析

	甲	乙	丙	丁
$\bar{x}$	8	9	9	8
S²	1	1.1	1.2	1.3