湖南省岳阳市华容县2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2021-07-23 类型:期末考试
一、单选题
-
1. 已知一个多边形的内角和是540°,则这个多边形是( )A、四边形 B、五边形 C、六边形 D、七边形2. 在以下”绿色食品、响应环保、可回收物、节水“四个标志图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列各点中,在第四象限的是( )A、(-5, 2) B、(5,-2) C、(-5,-2) D、(5,2)4. 下列函数中,y随x的增大而减少的函数是( )A、y=2x+8 B、y=-2+4x C、y=-2x+8 D、y=4x5. 给出下列命题,其中错误命题的个数是( )
3. 下列各点中,在第四象限的是( )A、(-5, 2) B、(5,-2) C、(-5,-2) D、(5,2)4. 下列函数中,y随x的增大而减少的函数是( )A、y=2x+8 B、y=-2+4x C、y=-2x+8 D、y=4x5. 给出下列命题,其中错误命题的个数是( )①四条边相等的四边形是正方形;
②四边形具有不稳定性;
③有两个锐角对应相等的两个直角三角形全等;
④一组对边平行的四边形是平行四边形.
A、1 B、2 C、3 D、46. 一列火车由甲市驶往相距600km的乙市,火车的速度是200km/时,火车离乙市的距离s(单位:km)随行驶时间t(单位:小时)变化的关系用图象表示正确的是( )A、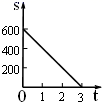 B、
B、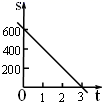 C、
C、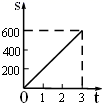 D、
D、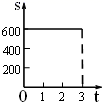 7. 有一张直角三角形纸片,两直角边长AC=6cm,BC=8cm,将△ABC折叠,使点B与点A重合,折痕为DE(如图),则CD则等于( )
7. 有一张直角三角形纸片,两直角边长AC=6cm,BC=8cm,将△ABC折叠,使点B与点A重合,折痕为DE(如图),则CD则等于( )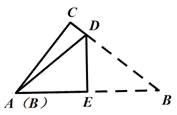 A、 B、 C、 D、8. 如图,分别以直角 的斜边AB , 直角边AC为边向 外作等边 和等边 ,F为AB的中点,DE与AB交于点G , EF与AC交于点H , , .给出如下结论:
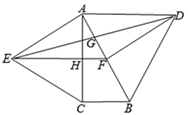
A、 B、 C、 D、8. 如图,分别以直角 的斜边AB , 直角边AC为边向 外作等边 和等边 ,F为AB的中点,DE与AB交于点G , EF与AC交于点H , , .给出如下结论:①EF⊥AC; ②四边形ADFE为菱形; ③ ; ④ ;
其中正确结论的是( )
 A、①②③ B、②③④ C、①③④ D、①②④
A、①②③ B、②③④ C、①③④ D、①②④二、填空题
-
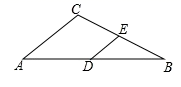
9. △ABC中,∠C=90°,∠A=54°,则∠B=°.10. 如图,在△ABC中,点D,E分别是边AB,BC的中点,若DE的长是6,则AC=.
 11. 将直线y=2x向下平移5个单位后,得到的直线解析式为 .12. 函数 中自变量x的取值范围是 .13. 如图:在 中,CD是斜边AB上的中线,若 ,则 .
11. 将直线y=2x向下平移5个单位后,得到的直线解析式为 .12. 函数 中自变量x的取值范围是 .13. 如图:在 中,CD是斜边AB上的中线,若 ,则 .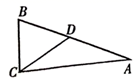 14.
14.如图,直线y=x+b与直线y=kx+6交于点P(3,5),则关于x的不等式x+b>kx+6的解集是 .
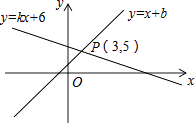 15. 如图,∠C=90°,AD平分∠BAC交BC于点D,若BC=5cm,BD=3cm,则D到AB的距离为.
15. 如图,∠C=90°,AD平分∠BAC交BC于点D,若BC=5cm,BD=3cm,则D到AB的距离为. 16. 如图,将边长为2的等边三角形沿x轴正方向连续翻折2016次,依次得到点P1 , P2 , P3 , …,P2016 , 则点P2016的坐标是 .
16. 如图,将边长为2的等边三角形沿x轴正方向连续翻折2016次,依次得到点P1 , P2 , P3 , …,P2016 , 则点P2016的坐标是 .
三、解答题
-
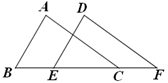
17. 已知y-3与x成正比例,当x=2时,y=7,求y与x之间的函数解析式.18. 已知:如图点B、E、C、F在同一条直线上,∠A=∠D=90°,AB=DE,BE=CF.求证:AC=DF.
 19. 已知:平行四边形ABCD的周长为18cm,对角线AC、BD相交于点O, 的周长比 DOA的周长小5cm,求这个平行四边形各边的长.
19. 已知:平行四边形ABCD的周长为18cm,对角线AC、BD相交于点O, 的周长比 DOA的周长小5cm,求这个平行四边形各边的长.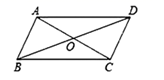 20. 湖南省作为全国第三批启动高考综合改革的省市之一,从2018年秋季入学的高中一年级学生开始实施高考综合改革.深化高考综合改革,承载着广大考生的美好期盼,事关千家万户的切身利益,社会关注度高.为了了解我市某小区居民对此政策的关注程度,某数学兴趣小组随机采访了该小区部分居民,根据采访情况制做了如统计图表:
20. 湖南省作为全国第三批启动高考综合改革的省市之一,从2018年秋季入学的高中一年级学生开始实施高考综合改革.深化高考综合改革,承载着广大考生的美好期盼,事关千家万户的切身利益,社会关注度高.为了了解我市某小区居民对此政策的关注程度,某数学兴趣小组随机采访了该小区部分居民,根据采访情况制做了如统计图表:关注程度
频数
频率
A.高度关注
m
0.4
B.一般关注
100
0.5
C.没有关注
20
n
 (1)、根据上述统计图表,可得此次采访的人数为 , m= , n=.(2)、根据以上信息补全图中的条形统计图.(3)、请估计在该小区1500名居民中,高度关注新高考政策的约有多少人?21. 如图,AC是▱ABCD的对角线,∠BAC=∠DAC.
(1)、根据上述统计图表,可得此次采访的人数为 , m= , n=.(2)、根据以上信息补全图中的条形统计图.(3)、请估计在该小区1500名居民中,高度关注新高考政策的约有多少人?21. 如图,AC是▱ABCD的对角线,∠BAC=∠DAC.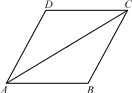 (1)、求证:AB=BC;(2)、若AB=2,AC=2 ,求▱ABCD的面积.22. 随着宁波市江北区慈城古县城旅游开发的推进,到慈城旅游的全国各地游客逐年上升.深受当地老百姓喜爱的两种本土特产杨梅和年糕,也深受外地游客的青睐.现在,有两种特产大礼包的组合是这样的:若购买2筐杨梅和3盒年糕,则需花费270元;若购买1筐杨梅和4盒年糕,则需花费260元.(杨梅、年糕分别按包装筐和包装盒计价)(1)、求一筐杨梅、一盒年糕的售价分别是多少元?(2)、如果需购买两种特产共12件(1筐或1盒称为1件),要求年糕的盒数不高于杨梅筐数的两倍,请你设计一种购买方案,使所需总费用最低.23. 如图,△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=DC,连接CF.
(1)、求证:AB=BC;(2)、若AB=2,AC=2 ,求▱ABCD的面积.22. 随着宁波市江北区慈城古县城旅游开发的推进,到慈城旅游的全国各地游客逐年上升.深受当地老百姓喜爱的两种本土特产杨梅和年糕,也深受外地游客的青睐.现在,有两种特产大礼包的组合是这样的:若购买2筐杨梅和3盒年糕,则需花费270元;若购买1筐杨梅和4盒年糕,则需花费260元.(杨梅、年糕分别按包装筐和包装盒计价)(1)、求一筐杨梅、一盒年糕的售价分别是多少元?(2)、如果需购买两种特产共12件(1筐或1盒称为1件),要求年糕的盒数不高于杨梅筐数的两倍,请你设计一种购买方案,使所需总费用最低.23. 如图,△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=DC,连接CF.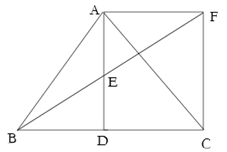 (1)、如果AB=AC,试猜想四边形ADCF的形状,并证明你的结论;(2)、△ABC满足什么条件时四边形ADCF为正方形,并证明你的结论.24.
(1)、如果AB=AC,试猜想四边形ADCF的形状,并证明你的结论;(2)、△ABC满足什么条件时四边形ADCF为正方形,并证明你的结论.24.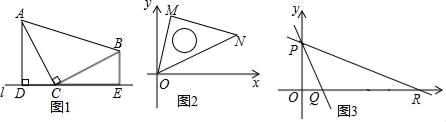 (1)、探索发现:如图1,已知Rt△ABC中,∠ACB=90°,AC=BC,直线l过点C,过点A作AD⊥l,过点B作BE⊥l,垂足分别为D、E.求证:AD=CE,CD=BE.(2)、迁移应用:如图2,将一块等腰直角的三角板MON放在平面直角坐标系内,三角板的一个锐角的顶点与坐标原点O重合,另两个顶点均落在第一象限内,已知点M的坐标为(1,3),求点N的坐标.(3)、拓展应用:如图3,在平面直角坐标系内,已知直线y=﹣3x+3与y轴交于点P,与x轴交于点Q,将直线PQ绕P点沿逆时针方向旋转45°后,所得的直线交x轴于点R.求点R的坐标.
(1)、探索发现:如图1,已知Rt△ABC中,∠ACB=90°,AC=BC,直线l过点C,过点A作AD⊥l,过点B作BE⊥l,垂足分别为D、E.求证:AD=CE,CD=BE.(2)、迁移应用:如图2,将一块等腰直角的三角板MON放在平面直角坐标系内,三角板的一个锐角的顶点与坐标原点O重合,另两个顶点均落在第一象限内,已知点M的坐标为(1,3),求点N的坐标.(3)、拓展应用:如图3,在平面直角坐标系内,已知直线y=﹣3x+3与y轴交于点P,与x轴交于点Q,将直线PQ绕P点沿逆时针方向旋转45°后,所得的直线交x轴于点R.求点R的坐标.