湖南省永州市2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2021-07-23 类型:期末考试
一、单选题
-
1. 函数 中自变量 的取值范围( )A、 B、 C、 D、2. 在平面坐标系中,位于第四象限的点是 ( )A、 B、 C、 D、3. 按照我国《生活垃圾管理条例》要求,到2025年底,我国地级及以上城市要基本建设垃圾类处理系统,下列垃圾分类指引标志图形中,是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 富有灿烂文化的永州,现今保留许多具有历史和文化价值的建筑,古朴的建筑物上雕刻的优美图案是我们数学研究的重要内容,图1中的“冰裂纹窗格”图案就是永州古建筑雕刻图案其中的代表,无规则多边形的形状,蕴含了丰富而和谐的数学美.图2是从图1冰裂纹窗格图案中提取的由五条线段组成的多边形,根据绘制的图案,则 的度数为( )
4. 富有灿烂文化的永州,现今保留许多具有历史和文化价值的建筑,古朴的建筑物上雕刻的优美图案是我们数学研究的重要内容,图1中的“冰裂纹窗格”图案就是永州古建筑雕刻图案其中的代表,无规则多边形的形状,蕴含了丰富而和谐的数学美.图2是从图1冰裂纹窗格图案中提取的由五条线段组成的多边形,根据绘制的图案,则 的度数为( ) A、 B、 C、 D、5. 如图是某组15名学生数学测试成绩的频数分布直方图,则成绩低于60分的人数是( )
A、 B、 C、 D、5. 如图是某组15名学生数学测试成绩的频数分布直方图,则成绩低于60分的人数是( ) A、3人 B、6人 C、10人 D、14人6. 如图,点D,E分别是 的边AB,AC的中点, ,则线段DE 的长为 ( )
A、3人 B、6人 C、10人 D、14人6. 如图,点D,E分别是 的边AB,AC的中点, ,则线段DE 的长为 ( ) A、1 B、2 C、3 D、47. 《九章算术》是我国古代第一部数学专著,它的出现标志中国古代数学形成了完整的体系.“折竹抵地”问题源自《九章算术》中:“今有竹高一丈,末折抵地,去本四尺,问折者高几何?”意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远(如图),则折断后的竹子高度为多少尺?(1丈=10尺)( )
A、1 B、2 C、3 D、47. 《九章算术》是我国古代第一部数学专著,它的出现标志中国古代数学形成了完整的体系.“折竹抵地”问题源自《九章算术》中:“今有竹高一丈,末折抵地,去本四尺,问折者高几何?”意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远(如图),则折断后的竹子高度为多少尺?(1丈=10尺)( )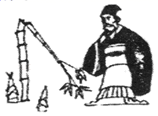 A、3 B、5 C、4.2 D、48. 下列说法正确的是( )A、一组对边相等,另一组对边平行的四边形是平行四边形 B、一组邻边相等的平行四边形是矩形 C、菱形有四条对称轴 D、对角线相等且互相垂直平分的四边形是正方形9. 如图,在 中, , , 是 的角平分线, ,则点 到线段 的距离为 ( )
A、3 B、5 C、4.2 D、48. 下列说法正确的是( )A、一组对边相等,另一组对边平行的四边形是平行四边形 B、一组邻边相等的平行四边形是矩形 C、菱形有四条对称轴 D、对角线相等且互相垂直平分的四边形是正方形9. 如图,在 中, , , 是 的角平分线, ,则点 到线段 的距离为 ( )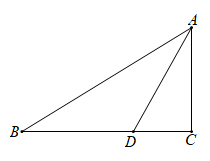 A、 B、1 C、2 D、410. 甲、乙两人在一次跨栏比赛中,路程s(m)与时间t(s)的函数关系如图所示,根据图形下列说法正确的个数为( )
A、 B、1 C、2 D、410. 甲、乙两人在一次跨栏比赛中,路程s(m)与时间t(s)的函数关系如图所示,根据图形下列说法正确的个数为( )①这次比赛的赛程是110米②甲先到达终点;③乙在这次比赛中的平均速度为 m/s;④乙的平均速度比甲快
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图,在 中, , , .
 12. “学习强国”是一款受大家青睐的在线学习政要应用软件,以深入学习宣传习近平新时代中国特色社会主义思想为主要内容,“学习强国”的英文是“Learningpower”,在这个词语中,英文字母“e”出现的频率是.13. 若点 , 都在正比例函数 的图象上,则 (填“>、<或=”).14. 如图,在菱形ABCD中, ,对角线 ,则菱形ABCD的面积为.
12. “学习强国”是一款受大家青睐的在线学习政要应用软件,以深入学习宣传习近平新时代中国特色社会主义思想为主要内容,“学习强国”的英文是“Learningpower”,在这个词语中,英文字母“e”出现的频率是.13. 若点 , 都在正比例函数 的图象上,则 (填“>、<或=”).14. 如图,在菱形ABCD中, ,对角线 ,则菱形ABCD的面积为. 15. 我市森林资源丰富,“云雾青峰绕,娥溪雪练飞”,大家知晓的高峰有舜皇山、阳明山、韭菜岭、九窽山,将其地理位置分别绘制在如图的网格中,若阳明山的位置坐标为 ,则舜皇山的位置坐标为 , 韭菜岭的位置坐标为 .
15. 我市森林资源丰富,“云雾青峰绕,娥溪雪练飞”,大家知晓的高峰有舜皇山、阳明山、韭菜岭、九窽山,将其地理位置分别绘制在如图的网格中,若阳明山的位置坐标为 ,则舜皇山的位置坐标为 , 韭菜岭的位置坐标为 . 16. 顺次连接对角线互相垂直的四边形的各边的中点所构成的四边形是.(填“平行四边形、矩形、菱形或正方形”)17. 如图,在平行四边形ABCD中, 的平分线 交 于点 ,连接 ,若 , ,则 .
16. 顺次连接对角线互相垂直的四边形的各边的中点所构成的四边形是.(填“平行四边形、矩形、菱形或正方形”)17. 如图,在平行四边形ABCD中, 的平分线 交 于点 ,连接 ,若 , ,则 . 18. 如图,在平行四边形ABCD中, , 于点 ,点 、 分别是 、 的中点,连接 、 、 ,下列四种说法:① ;②四边形ABGF是菱形;③ ;④ ,正确的有.(填序号)
18. 如图,在平行四边形ABCD中, , 于点 ,点 、 分别是 、 的中点,连接 、 、 ,下列四种说法:① ;②四边形ABGF是菱形;③ ;④ ,正确的有.(填序号)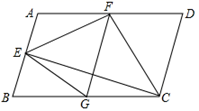
三、解答题
-
19. 在平面直角坐标系中, 的位置如图所示,已知点A的坐标是 .
 (1)、点C关于y轴对称的点的坐标( , );(2)、将三角形 向右平移2个单位,得到它的像为 ,请在图中画出 的图形;(3)、 的面积 .20. 如图,点D为BC的中点, 于点 , 于点 ,且 ,求证: .
(1)、点C关于y轴对称的点的坐标( , );(2)、将三角形 向右平移2个单位,得到它的像为 ,请在图中画出 的图形;(3)、 的面积 .20. 如图,点D为BC的中点, 于点 , 于点 ,且 ,求证: .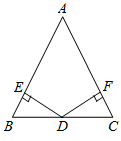 21. 如图,在 中, ,点 为斜边 边上的中点, , .
21. 如图,在 中, ,点 为斜边 边上的中点, , . (1)、求证:四边形ADCE是菱形(2)、连接DE,若 , .求证: 是等边三角形.22. 某校为了了解八年级学生的近视情况,对八年级的学生进行了一次视力抽样调查,并将调查的数据进行统计整理,绘制出如下的频数分布表和频数分布直方图.
(1)、求证:四边形ADCE是菱形(2)、连接DE,若 , .求证: 是等边三角形.22. 某校为了了解八年级学生的近视情况,对八年级的学生进行了一次视力抽样调查,并将调查的数据进行统计整理,绘制出如下的频数分布表和频数分布直方图.
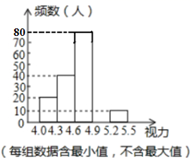 (1)、在频数分布表,则 , ;(2)、将频数分布直方图补充完整;(3)、若视力在4.6以上(含4.6)均属正常,求视力正常的人数占被调查人数的百分比.23. 由于持续高温和连日无雨,某水库的蓄水量随着时间的增加而减少,蓄水量y(万立方米)与 干旱时间t(天)之间的关系如图所示,回答下列问题:
(1)、在频数分布表,则 , ;(2)、将频数分布直方图补充完整;(3)、若视力在4.6以上(含4.6)均属正常,求视力正常的人数占被调查人数的百分比.23. 由于持续高温和连日无雨,某水库的蓄水量随着时间的增加而减少,蓄水量y(万立方米)与 干旱时间t(天)之间的关系如图所示,回答下列问题: (1)、干旱持续到第10天,水库的蓄水量为万立方米.(2)、若水库的蓄水量小于360万立方时,将发生严重干旱警报,那么多少天后将发生严重干旱警报?(3)、在(2)的条件下,照这样干旱下去,预计再持续多少天,水库将干涸.24. 如图,在直线 上将正方形ABCD和正方形ECFG的边CD和边CE靠在一起,连接DG,过点A作 ,交BG于点H,连接HF,AF,其中FH交DG于点M.
(1)、干旱持续到第10天,水库的蓄水量为万立方米.(2)、若水库的蓄水量小于360万立方时,将发生严重干旱警报,那么多少天后将发生严重干旱警报?(3)、在(2)的条件下,照这样干旱下去,预计再持续多少天,水库将干涸.24. 如图,在直线 上将正方形ABCD和正方形ECFG的边CD和边CE靠在一起,连接DG,过点A作 ,交BG于点H,连接HF,AF,其中FH交DG于点M. (1)、求证: 为等腰直角三角形.(2)、若 , ,求DM的长.25. 背景知识:已知两直线 , ,若 ,则 ;若 ,则 .
(1)、求证: 为等腰直角三角形.(2)、若 , ,求DM的长.25. 背景知识:已知两直线 , ,若 ,则 ;若 ,则 .应用:在平面直线坐标系 中,直线 交x轴于点C,交y轴于点D,若 于点 ,交y轴于点A,交x轴于点B.
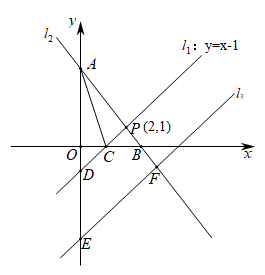 (1)、求直线 的表达式;(2)、求 的面积;(3)、若将直线 向下平移 个单位,得到新的直线 ,交y轴于点E,交直线 于点F,使得 ,求 的值.26. 如下图1,在平面直角坐标系中 中,将一个含 的直角三角板如图放置,直角顶点与原点重合,若点A的坐标为 , .
(1)、求直线 的表达式;(2)、求 的面积;(3)、若将直线 向下平移 个单位,得到新的直线 ,交y轴于点E,交直线 于点F,使得 ,求 的值.26. 如下图1,在平面直角坐标系中 中,将一个含 的直角三角板如图放置,直角顶点与原点重合,若点A的坐标为 , .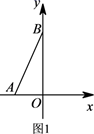 (1)、旋转操作:如下图2,将此直角三角板绕点O顺时针旋转 时,则点B的坐标为.
(1)、旋转操作:如下图2,将此直角三角板绕点O顺时针旋转 时,则点B的坐标为. (2)、问题探究:在图2的基础上继续将直角三角板绕点O顺时针 ,如图3,在AB边上的上方以AB为边作等边 ,问:是否存在这样的点D,使得以点A、B、C、D四点为顶点的四边形构成为菱形,若存在,请直接写出点D所有可能的坐标;若不存在,请说明理由.
(2)、问题探究:在图2的基础上继续将直角三角板绕点O顺时针 ,如图3,在AB边上的上方以AB为边作等边 ,问:是否存在这样的点D,使得以点A、B、C、D四点为顶点的四边形构成为菱形,若存在,请直接写出点D所有可能的坐标;若不存在,请说明理由. (3)、动点分析:在图3的基础上,过点O作 于点P,如图4,若点F是边OB的中点,点M是射线PF上的一个动点,当 为直角三角形时,求OM的长.
(3)、动点分析:在图3的基础上,过点O作 于点P,如图4,若点F是边OB的中点,点M是射线PF上的一个动点,当 为直角三角形时,求OM的长.
