湖南省益阳市赫山区2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2021-07-23 类型:期末考试
一、单选题
-
1. 下列几组数中,能作为直角三角形三边长度的是( )A、2,3,4 B、4,4,5 C、5,6,7 D、5,12,132. 剪纸是扬州的非物质文化遗产之一,下列剪纸作品中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 若一个多边形的每个内角都等于150°,则这个多边形的边数是( )A、10 B、11 C、12 D、134. 顺次连接矩形四边中点得到的四边形一定是( )A、梯形 B、正方形 C、矩形 D、菱形5. 在平面直角坐标系中,点P(﹣3,4)关于x轴的对称点的坐标是( )A、(﹣4,﹣3) B、(﹣3,﹣4) C、(3,4) D、(3,﹣4)6. 在平面直角坐标系中, ▱ABCD的顶点A(0,0),B(5,0),D(2,3),则顶点C的坐标是( )A、(3,7) B、(5,3) C、(7,3) D、(8,2)7. 小红把一枚硬币抛掷10次,结果有4次正面朝上,那么( )A、正面朝上的频数是0.4 B、反面朝上的频数是6 C、正面朝上的频率是4 D、反面朝上的频率是68. 如图,CD是△ABC的边AB上的中线,且CD= AB,则下列结论错误的是( )
3. 若一个多边形的每个内角都等于150°,则这个多边形的边数是( )A、10 B、11 C、12 D、134. 顺次连接矩形四边中点得到的四边形一定是( )A、梯形 B、正方形 C、矩形 D、菱形5. 在平面直角坐标系中,点P(﹣3,4)关于x轴的对称点的坐标是( )A、(﹣4,﹣3) B、(﹣3,﹣4) C、(3,4) D、(3,﹣4)6. 在平面直角坐标系中, ▱ABCD的顶点A(0,0),B(5,0),D(2,3),则顶点C的坐标是( )A、(3,7) B、(5,3) C、(7,3) D、(8,2)7. 小红把一枚硬币抛掷10次,结果有4次正面朝上,那么( )A、正面朝上的频数是0.4 B、反面朝上的频数是6 C、正面朝上的频率是4 D、反面朝上的频率是68. 如图,CD是△ABC的边AB上的中线,且CD= AB,则下列结论错误的是( )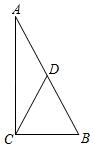 A、AD=BD B、∠A=30° C、∠ACB=90° D、AC2+BC2=AB29. 正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是( )A、
A、AD=BD B、∠A=30° C、∠ACB=90° D、AC2+BC2=AB29. 正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是( )A、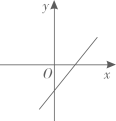 B、
B、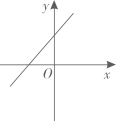 C、
C、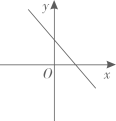 D、
D、 10. 如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A , 则不等式0<kx+b<2x的解集为( )
10. 如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A , 则不等式0<kx+b<2x的解集为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
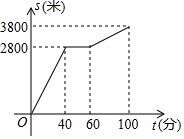
-
11. 如图,在△ABC中,∠C=90°,AD平分∠CAB,BC=6,BD=4,则点D到AB的距离是.
 12. 五边形从某一个顶点出发可以引条对角线.13. 已知菱形的两对角线长分别为6cm和8cm,则菱形的面积为cm2.14. 将点P (﹣3,4)先向下平移3个单位,再向右平移2个单位后得到点Q,则点Q的坐标是.15. 在函数y= 中,自变量x的取值范围是.16. 今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.则下列说法中,正确的序号为.
12. 五边形从某一个顶点出发可以引条对角线.13. 已知菱形的两对角线长分别为6cm和8cm,则菱形的面积为cm2.14. 将点P (﹣3,4)先向下平移3个单位,再向右平移2个单位后得到点Q,则点Q的坐标是.15. 在函数y= 中,自变量x的取值范围是.16. 今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.则下列说法中,正确的序号为.①小明中途休息用了20分钟.
②小明休息前爬山的平均速度为每分钟70米.
③小明在上述过程中所走的路程为6600米.
④小明休息前爬山的平均速度大于休息后爬山的平均速度.
 17. 一次函数y=kx+b(k≠0)中,x与y的部分对应值如下表:
17. 一次函数y=kx+b(k≠0)中,x与y的部分对应值如下表:x
-2
-1
0
1
2
y
9
6
3
0
-3
那么,一元一次方程kx+b=0在这里的解为.
18. 如图Rt△ABC中,∠BAC=90°,AB=3,AC=4,点P为BC上任意一点,连接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为.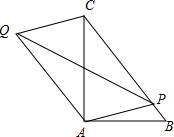
三、解答题
-
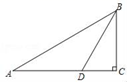
19. 如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,CD=5cm,求AB的长.
 20. 如图,矩形 的对角线 垂直平分线与边 、 分别交于点 ,求证:四边形 为菱形.
20. 如图,矩形 的对角线 垂直平分线与边 、 分别交于点 ,求证:四边形 为菱形.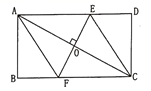 21. 在平面直角坐标系xOy中,已知直线l:y=kx+b(k≠0经过点A(﹣4,0),与y轴交于点B,如果△AOB的面积为4,求直线l的表达式.22. 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
21. 在平面直角坐标系xOy中,已知直线l:y=kx+b(k≠0经过点A(﹣4,0),与y轴交于点B,如果△AOB的面积为4,求直线l的表达式.22. 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△ ;
(2)请画出△ABC关于原点对称的△ ;
;
(3)在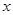 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.23. 某班同学为了解2019年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.
轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.23. 某班同学为了解2019年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理.月均用水量
频数
频率
0<x≤5
6
0.12
5<x≤10
m
0.24
10<x≤15
16
0.32
15<x≤20
10
0.20
20<x≤25
4
n
25<x≤30
2
0.04

请解答以下问题:
(1)、求出上面的频数分布表中的m、n的值,并把频数分布直方图补充完整;(2)、求该小区用水量不超过15t的家庭占被调查家庭总数的百分比;(3)、若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过10t的家庭大约有多少户?24. 阅读与探究我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.请结合上述阅读材料,解决下列问题:
 (1)、在我们所学过的特殊四边形中,是勾股四边形的是 (任写一种即可);(2)、图1、图2均为 的正方形网格,点 均在格点上,请在图中标出格点 ,连接 ,使得四边形 符合下列要求:图1中的四边形 是勾股四边形,并且是轴对称图形;图2中的四边形 是勾股四边形且对角线相等,但不是轴对称图形.25. 如图,已知四边形ABCD是正方形,点E、F分别在AD、DC上,BE与AF相交于点G,且BE=AF.
(1)、在我们所学过的特殊四边形中,是勾股四边形的是 (任写一种即可);(2)、图1、图2均为 的正方形网格,点 均在格点上,请在图中标出格点 ,连接 ,使得四边形 符合下列要求:图1中的四边形 是勾股四边形,并且是轴对称图形;图2中的四边形 是勾股四边形且对角线相等,但不是轴对称图形.25. 如图,已知四边形ABCD是正方形,点E、F分别在AD、DC上,BE与AF相交于点G,且BE=AF.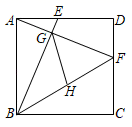 (1)、求证:△ABE≌△DAF;(2)、求证:BE⊥AF;(3)、如果正方形ABCD的边长为5,AE=2,点H为BF的中点,连接GH.求GH的长.26. 如表是某摩托车厂2019年前3个月摩托车各月产量:
(1)、求证:△ABE≌△DAF;(2)、求证:BE⊥AF;(3)、如果正方形ABCD的边长为5,AE=2,点H为BF的中点,连接GH.求GH的长.26. 如表是某摩托车厂2019年前3个月摩托车各月产量:x(月)
1
2
3
y(辆)
550
600
650
(1)、根据表格中的数据,求y(辆)与x(月)之间的函数表达式;(2)、按照此趋势,你能预测该摩托车厂2019年4月摩托车月产量吗?(3)、能够利用(1)中所建立函数模型预测2019年12月摩托车月产量吗?为什么?