湖南省娄底市2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2021-07-23 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个图形，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列长度的三条线段能组成直角三角形的是（）

A、2，3，4 B、3，4，5 C、4，5，6 D、6，8，11

查看试题解析
3. 如图，在△ABC中，∠ACB＝90°，CD⊥AB于点D，∠A＝30°，BD＝2，则AD的长度是（）

A、6 B、8 C、12 D、16

查看试题解析
4. 如图，已知 $A C ⊥ B D$ ，垂足为 $O$ ， $A O = C O$ ， $A B = C D$ ，则可得到 $Δ A O B ≅ Δ C O D$ ，理由是（）

A、 $H L$ B、 $S A S$ C、 $A S A$ D、 $A A S$

查看试题解析
5. 如图，在 ABCD中，BE平分∠ABC，交AD于点E，AE=3，ED=1，则ABCD的周长为（）

A、10 B、12 C、14 D、16

查看试题解析
6. 一个多边形的边数每增加一条，这个多边形的（）

A、内角和增加360° B、外角和增加360° C、对角线增加一条 D、内角和增加180°

查看试题解析
7. 已知P（2-x，3x-4）到两坐标轴的距离相等，则x的值为（）

A、 $\frac{3}{2}$ B、 $- 1$ C、 $\frac{3}{2}$ 或 $- 1$ D、 $\frac{3}{2}$ 或1

查看试题解析
8. 下列说法中，不正确是（　　）

A、对角线互相平分的四边形是平行四边形 B、两组对角分别相等的四边形是平行四边形 C、一组对边平行且相等的四边形是平行四边形 D、一组对边平行另一组对边相等的四边形是平行四边形

查看试题解析
9. 一次函数 $y = (k + 2) x + k^{2} - 4$ 的图象经过原点，则k的值为 $($ $)$

A、2 B、 $- 2$ C、2或 $- 2$ D、3

查看试题解析
10. 在平面直角坐标系中，一次函数y=kx+b的图象如图所示，则k和b的取值范围是（）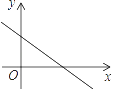

A、k＞0，b＞0 B、k＞0，b＜0 C、k＜0，b＞0 D、k＜0，b＜0

查看试题解析
11. 在全民健身环城越野赛中，甲乙两选手的行程y（千米）随时间（时）变化的图象（全程）如图所示.有下列说法：①起跑后1小时内，甲在乙的前面；②第1小时两人都跑了10千米；③甲比乙先到达终点；④两人都跑了20千米.其中正确的说法有（）

A、1 个 B、2 个 C、3 个 D、4个

查看试题解析
12. 如图，把矩形ABCD沿EF折叠，使点C落在点A处，点D落在点G处，若∠CFE=60°，且DE=1，则边BC的长（）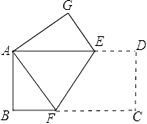

A、3 B、4 C、3.5 D、6

查看试题解析

二、填空题

13. 将50个数据分成5组列出频数分布表，其中第一组的频数是6，第二组与第五组的频数和为20，第三组的频率为0.2，则第四组的频数为.

查看试题解析
14. 直线 $y = - 2 x + 1$ 过第象限，且 $y$ 随 $x$ 的增大而.

查看试题解析
15. 如图，在平面直角坐标系xOy中，若菱形ABCD的顶点A，B的坐标分别为（﹣3，0），（2，0），点D在y轴上，则点C的坐标是．

查看试题解析
16. 如图，在 $R t Δ A B C$ 中， $∠ A C B = 90^{\circ}$ ，AD平分 $∠ B A C$ 交BC于点D，若 $A B = 5$ ， $D C = 2$ ，则 $Δ A B D$ 的面积为.

查看试题解析
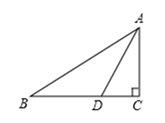17. 如图，在 $R t Δ A B C$ 中，点D，E，F分别是AB，AC，BC的中点，若CD=8，则EF的长为.

查看试题解析
18. 在抗击新冠肺炎的斗争中，娄底市根据疫情的发展情况，决定全市中小学延期开学，并采用线上教学的形式，真正做到停课不停学，某中学初二1班全体同学自主完成学习任务的同时，不忘关心同学的安危，在停课不停学期间全班每两个同学都通过一次电话，我们可以把该班人数n与通话次数S间的关系用下列模型表示：问：若该班有50名同学，则它们之间共通了次电话；

查看试题解析

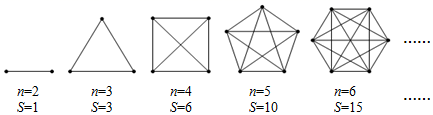
三、解答题

19. 如图， $Δ A B C$ 在直角坐标系中，

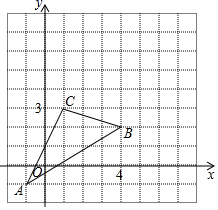(1)、请写出 $Δ A B C$ 各顶点的坐标

(2)、若把向上平移2个单位，再向右平移3个单位得到 $Δ A_{1} B_{1} C_{1}$ ，请在图上画出，并写出 $A_{1} ， B_{1} ， C_{1}$ 的坐标；

(3)、求出 $Δ A B C$ 的面积

查看试题解析

20. 为讴歌抗击新冠肺炎的白衣天使，某校举行了新时代最可爱的人征文比赛，已知每篇参赛征文成绩记a分

(60 \leq a \leq 100)

，组委会统计了他们的比赛成绩，并根据成绩绘制了如下的不完整的统计图表

请根据所给信息回答下列问题

成绩	频数	频率
$60 \leq a < 70$	24	0.3
$70 \leq a < 80$	m	0.4
$80 \leq a < 90$	16	n
$90 \leq a \leq 100$	8	0.1

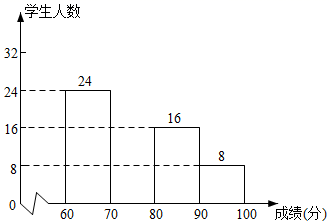(1)、参加征文比赛的共有多少人？

(2)、在频数分布表中，m=；n=.

(3)、补全图中的频数分别直方图.

查看试题解析

21. 某学校要对如图所示的一块地进行绿化，已知 $A D = 4 m$ ， $C D = 3 m$ ， $A D ⊥ D C$ ， $A B = 13 m$ ， $B C = 12 m$ ，求这块地的面积.

查看试题解析
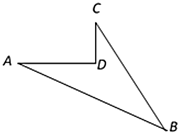22. EF是平行四边ABCD的对角线BD的垂直平分线，EF与边AD ， BC分别交于点E ， F ．

(1)、求证：四边形BFDE是菱形；

(2)、若ED=5，BD=8，求菱形BFDE的面积．

查看试题解析
23. 甲、乙两家蓝莓采摘园的草莓品质相同，销售价格都是每千克30元，“五一”假期，两家均推出了优惠方案，甲采摘园的优惠方案是：游客进园购买60元的门票，采摘的蓝莓六折优惠；乙采摘园的优惠方案是：游客进园不需购买门票，采摘的蓝莓超过10千克后，超过部分五折优惠，优惠期间，设某游客的蓝莓采摘量为 $x$ （千克），在甲采摘园所需总费用为 $y_{1}$ （元），在乙采摘园所需总费用为 $y_{2}$ （元）.

(1)、当采摘量超过10千克时，求 $y_{1} ， y_{2}$ 与 $x$ 的关系式；

(2)、若要采摘40千克蓝莓，去哪家比较合算？请计算说明.

查看试题解析
24. 在一条笔直的公路上有两个停靠站，公路旁有一块地正在开发，现在C处时常需要爆破作业，如图，已知A，B两站相距2km，且 $∠ A B C = 30 ° ， ∠ B A C = 60 °$ ，为安全起见，爆破点C周围半径500米范围内任何人不得进入，问在进行爆破时，公路AB段是否需要暂时封闭？请说明理由（ $\sqrt{3} = 1.73$ ）

查看试题解析
25. 如图，已知过点B（1，0）的直线 $l_{1}$ 与直线 $l_{2}$ ： $y = 2 x + 4$ 相交于点P（－1，a）.且l₁与y轴相交于C点，l₂与x轴相交于A点.

(1)、求直线 $l_{1}$ 的解析式；

(2)、求四边形 $P A O C$ 的面积；

(3)、若点Q是x轴上一动点，连接PQ、CQ，当△QPC周长最小时，求点Q坐标.

查看试题解析
26. 如图1，对角线互相垂直的四边形叫做垂美四边形.

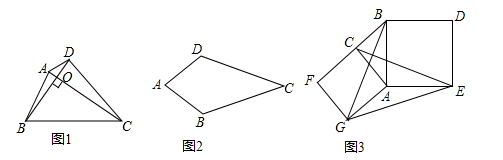(1)、概念理解：如图2，在四边形 $A B C D$ 中， $A B = A D$ ， $C B = C D$ ，问四边形 $A B C D$ 是垂美四边形吗？请说明理由；

(2)、性质探究：如图1，四边形 $A B C D$ 的对角线 $A C$ 、 $B D$ 交于点 $O$ ， $A C ⊥ B D$ .试证明： $A B^{2} + C D^{2} = A D^{2} + B C^{2}$ ；

(3)、解决问题：如图3，分别以 $R t △ A C B$ 的直角边 $A C$ 和斜边 $A B$ 为边向外作正方形 $A C F G$ 和正方形 $A B D E$ ，连结 $C E$ 、 $B G$ 、 $G E$ .已知 $A C = 4$ ， $A B = 5$ ，求 $G E$ 的长.

查看试题解析