湖南省涟源市2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2021-07-23 类型：期末考试

进入出卷网下载

一、单选题

1. 下列函数中，是正比例函数的是（）

A、 $y = 8 x$ B、 $y = \frac{- 8}{x}$ C、 $y = 5 x^{2} + 6$ D、 $y = - 0.5 x - 1$

查看试题解析
2. 在下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. “早发现，早报告，早隔离，早治疗”是我国抗击“新冠肺炎”的宝贵经验，其中“早”字出现的频率是（）

A、 $\frac{1}{12}$ B、 $\frac{1}{4}$ C、 $\frac{2}{3}$ D、 $\frac{1}{3}$

查看试题解析
4. 如图，在 $▱ A B C D$ 中，全等三角形的对数共有（）

A、2对 B、3对 C、4对 D、5对

查看试题解析
5. 在函数 $y = \sqrt{x + 1}$ 中，自变量 $x$ 的取值范围是（）

A、 $x > - 1$ B、 $x \leq - 1$ C、 $x \neq - 1$ D、 $x \geq - 1$

查看试题解析
6. 若一个凸多边形的内角和为720°，则这个多边形的边数为 $($ 　　 $)$

A、4 B、5 C、6 D、7

查看试题解析
7. 矩形具有而平行四边形不一定具有的性质是（）

A、对边相等 B、对角相等 C、对角线相等 D、对角线互相平分

查看试题解析
8. 已知点 $P (a ， 1)$ 在一、三象限的角平分线上，则 $a$ 的值为（）

A、 $- 1$ B、0 C、1 D、2

查看试题解析
9. 将等腰直角三角形纸片和矩形纸片按如图方式折叠放在一起，若 $∠ 1 = 30 °$ ，则 $∠ 2$ 的度数为（）

A、 $10 °$ B、 $15 °$ C、 $20 °$ D、 $30 °$

查看试题解析
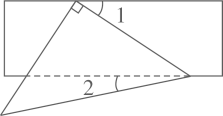10. 如图，菱形ABCD的对角线AC、BD的长分别为6和8，则这个菱形的周长是（）。

A、20 B、24 C、40 D、48

查看试题解析
11. 如图，已知 $B D$ 是 $△ A B C$ 的角平分线， $E D$ 是 $B C$ 的垂直平分线， $∠ B A C = 90 °$ ， $A D = 3$ ，则 $C E$ 的长为（）

A、6 B、5 C、4 D、 $3 \sqrt{3}$

查看试题解析
12. 如图，已知 $Δ A B C$ 周长为1，连接 $Δ A B C$ 三边的中点构成第二个三角形，再连接第二个三角形三边中点构成第三个三角形，依此类推，则第2020个三角形的周长是（）

A、 $\frac{1}{2^{2019}}$ B、 $\frac{1}{2^{2020}}$ C、 $\frac{1}{2019}$ D、 $\frac{1}{2020}$

查看试题解析

二、填空题

13. 如图，在 $R t Δ A B C$ 中， $∠ B = 90 °$ ， $∠ A C D = 130 °$ ， $∠ A =$ .

查看试题解析
14. 在平面直角坐标系中，点 $M (a ， b)$ 与点 $N (3 ， - 1)$ 关于 $x$ 轴对称，则 $a + b$ 的值是．

查看试题解析
15. 如图， $∠ C = ∠ D = 90 °$ ，请添加一个条件，使 $R t Δ A B C$ 与 $R t Δ A B D$ 全等.你添加的条件是（写出一个符合要求的条件即可）.

查看试题解析
16. 将直线 $y = 2 x$ 向上平移3个单位，所得直线的表达式为.

查看试题解析
17. 若点 $A (1 - m ， m - 2)$ 在第三象限，那么 $m$ 的值满足.

查看试题解析
18. 如图，两个边长均为6的正方形重叠在一起， $O$ 是正方形 $A B C D$ 的中心，则阴影部分的面积是.

查看试题解析

三、解答题

19. 已知直线 $y = - 2 x + b$ 与 $x$ 轴交于点 $A (- 3 ， 0)$ ，求这条直线与 $y$ 轴的交点坐标.

查看试题解析
20. 在平面直角坐标系中，画出以 $A (- 1 ， 2)$ ， $B (- 3 ， - 2)$ ， $C (3 ， - 3)$ 为顶点的三角形，并求 $Δ A B C$ 的面积.

查看试题解析

21. 八甲班进行了一次数学考试，将成绩绘制成了如下不完整的频数分布表和频数直方图：

成绩	频数（人数）	频率
$50 \leq x < 60$	5	0.1
$60 \leq x < 70$	10	0.2
$70 \leq x < 80$	20	0.4
$80 \leq x < 90$	$a$	0.2
$90 \leq x < 100$	5	$b$

(1)、求频数分布表中

a

和

b

的值；

(2)、将频数直方图补充完整；

(3)、成绩不低于60分为及格，该班本次数学考试的及格率是多少？

查看试题解析

22. 如图，一艘渔船以40海里/小时的速度由西向东追赶鱼群，在 $A$ 处测得小岛 $C$ 在渔船的北偏东 $60 °$ 方向；半小时后，渔船到达 $B$ 处，此时测得小岛 $C$ 在渔船的北偏东 $30 °$ 方向.已知以小岛 $C$ 为中心，周围18海里以内为军事演习着弹危险区.如果这艘渔船继续向东追赶鱼群，是否有着弹危险？

查看试题解析
23. 根据民航通用规定，搭乘国内航班的每位旅客都有免费行李额，行李超重部分需按统一计价标准支付超重行李费，超重行李费 $y$ （元）是行李质量 $x$ （千克）的一次函数.搭乘某航班，已知行李质量为30千克时需支付超重行李费150元，行李质量为40千克时需支付超重行李费300元.

(1)、求该航班 $y$ 与 $x$ 之间的函数表达式；

(2)、每位旅客的免费行李额是多少千克？

查看试题解析
24. 如图，在平行四边形 $A B C D$ 中，对角线 $A C$ 与 $B D$ 相交于点 $O$ ，点 $E ， F$ 分别为 $O B$ ， $O D$ 的中点，延长 $A E$ 至 $G$ ，使 $E G = A E$ ，连接 $C G$ .

(1)、求证： $Δ A B E ≌ Δ C D F$ ；

(2)、当 $A C = 2 A B$ 时，四边形 $E G C F$ 是什么样的四边形？试说明理由.

查看试题解析
25. 如图，△AOB是边长为2的等边三角形，过点A的直线 $y = - \frac{\sqrt{3}}{3} x + m$ 与x轴交于点C.

(1)、求点A的坐标；

(2)、求直线AC的解析式；

(3)、求证：OA⊥AC.

查看试题解析
26. 如图，在平行四边形 $A B C D$ 中， $∠ B A D$ 的平分线交 $B C$ 于点 $E$ ，交 $D C$ 的延长线于 $F$ ，以 $E C$ 、 $C F$ 为邻边作平行四边形 $E C F G$ .

(1)、求证：四边形 $E C F G$ 是菱形；

(2)、连结 $B D$ 、 $C G$ ，若 $∠ A B C = 120 °$ ，则 $Δ B D G$ 是等边三角形吗？为什么？

(3)、若 $∠ A B C = 90 °$ ， $A B = 10$ ， $A D = 24$ ， $M$ 是 $E F$ 的中点，求 $D M$ 的长.

查看试题解析