湖南省常德市2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期：2021-07-23 类型：期末考试
一、单选题
-
1. 下列图案中，是轴对称图形而不是中心对称图形的是（ ）A、
B、
C、
D、
2. 将50个数据分成5组列出频数分布表，其中第二组的频数为15，则第二组的频率为（ ）A、0.28 B、0.3 C、0.4 D、0.23. 下列各曲线中表示y是x的函数的是（ ）A、
B、
C、
D、
4. 点Q（3m，2m﹣2）在x轴上，则m的值为（ ）A、0 B、1 C、﹣1 D、﹣35. 在Rt△ABC中，∠C＝90°，若c＝10cm，a：b＝3：4，则△ABC的周长（ ）A、12cm B、20cm C、24cm D、48cm6. 一次函数y＝﹣4x+2的图象不经过（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 如图，在△ABC中，AB＝AC＝3，BC＝4，AE平分∠BAC交BC于点E，点D为AB的中点，连接DE，则△BDE的周长是（ ）
A、3 B、4 C、5 D、68. 如图，正方形ABCD的边长为6，点E、F分别在AB，AD上，若CE=3 ，且∠ECF=45°，则CF长为（ ）
A、2 B、3 C、 D、二、填空题
-
9. 如图， 中， ， ，则点 的坐标为.
10. 已知y＝3x+m+3是正比例函数，则m＝.11. 从一个 边形的同一个顶点出发，分别连结这个顶点与其余各顶点，若把这个多边形分割为 个三角形，则 的值是.12. 如图，在Rt△ABC中，∠C＝90°，AB＝5，则正方形ADEC与正方形BCFG的面积之和为.
13. 若一次函数的图象是由直线y＝﹣2x向上平移3个单位所得，则该一次函数的表达式为.14. 如图所示是某班学生体重的频数分布直方图，则该班学生体重不足45千克的有人.（注：35～40千克包括35千克，不包括40千克，其他同）.
15. 在平面直角坐标系中，等边△ABC的顶点A（﹣3，0），B（3，0），则顶点C的坐标为.16. 如图，在锐角三角形ABC中，BC＝6 ，∠ABC＝45°，BD平分∠ABC，M、N分别是BD、BC上的动点，则CM+MN的最小值是.
三、解答题
-
17. 已知一次函数y＝kx+3的图象经过点（1，﹣3）.(1)、求一次函数的表达式；(2)、已知点（a，4）在该函数的图象上，求a的值.18. 如图，在平行四边形ABCD中，M、N分别是OA，OC的中点，O为对角线AC与BD的交点，请证明DM∥BN.
19. 如图，在平面直角坐标系中有三个点A（－3，2）、B（﹣5，1）、C（－2，0），P（a，b）是△ABC的边AC上一点，△ABC经平移后得到△A1B1C1 ， 点P的对应点为P1（a+6，b+2）.
(1)、画出平移后的△A1B1C1 ，(2)、写出点A1、B1 、C1、的坐标；.(3)、求四边形ACC1A1的面积.20. 某天早晨，王老师从家出发步行前往学校，途中在路边一饭店吃早餐，如图所示是王老师从家到学校这一过程中的所走路程s(米)与时间t(分)之间的关系．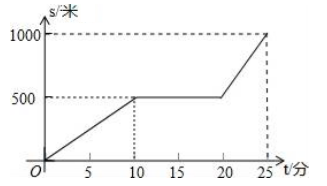
(1)、学校离他家米，从出发到学校，王老师共用了分钟；(2)、王老师吃早餐用了多少分钟？(3)、王老师吃早餐以前的速度快还是吃完早餐以后的速度快？吃完早餐后的平均速度是多少？21. 如图，已知B，D在线段AC上，且AD＝CB，BF＝DE，∠AED＝∠CFB＝90°
求证：
(1)、BE∥DF.(2)、△AED≌△CFB；22. 如图，在△ABC中，∠C＝90°，将△ACE沿着AE折叠以后C点正好落在AB边上的点D处.
(1)、当∠B＝28°时，求∠CAE的度数；(2)、当AC＝6，AB＝10时，求线段DE的长.23. 2020年3月25日是全国中小学生安全教育日，常德芷兰实验学校为加强学生的安全意识，组织了全校8000名学生参加安全知识竞赛，从中抽取了部分学生成绩进行统计.请根据尚未完成的频率分布表和频数分布直方图解题.频率分布表
分数段
频数
频率
50.5～60.5
16
0.08
60.5～70.5
40
0.2
70.5～80.5
50
0.25
80.5～90.5
m
0.35
90.5～100.5
24
n
(1)、这次抽取了名学生的竞赛成绩进行统计，其中：m＝ ， n＝；(2)、补全频数分布直方图.(3)、若成绩在70分以下（含70分）的学生为安全意识不强，有待进一步加强安全教育，则该校安全意识不强的学生约有多少人？24. 如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD，等边△ABE.已知∠BAC=30°，EE⊥AB，垂足为F，连接DF；
求证：
(1)、四边形ADFE是平行四边形；(2)、AC⊥DF；(3)、AC=EF；25. 如图，直线 分别交x轴、y轴于A、B两点，直线BC与x轴交于点 ，P是线段AB上的一个动点 点P与A、B不重合 .
(1)、求直线BC所对应的的函数表达式；(2)、设动点P的横坐标为t， 的面积为S.①求出S与t的函数关系式，并写出自变量t的取值范围；
②在线段BC上存在点Q，使得四边形COPQ是平行四边形，求此时点Q的坐标.
26. 在正方形ABCD中.
(1)、如图1，点E、F分别在BC、CD上，AE、BF相交于点O，∠AOB=90°，试判断AE与BF的数量关系，并说明理由；(2)、如图2，点E、F、G、H分别在边BC、CD、DA、AB上，EG、FH相交于点O，∠GOH=90°，且EG=7，求FH的长；(3)、如图3，点E、F分别在BC、CD上，AE、BF相交于点O，∠AOB=90°，若AB=5，图中阴影部分的面积与正方形的面积之比为4：5，求△ABO的周长.