海南省临高县2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2021-07-23 类型:期末考试
一、单选题
-
1. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、2. 下列各组线段中,不能构成直角三角形的三边的是( )A、 B、 C、 D、3. 一组数据: 则这组数据的中位数和众数分别是( )A、 B、 C、 D、4. 一个正比例函数的图象经过(2,-1),则它的表达式为 )A、y=-2x B、y=2x C、 D、5. 下列说法中正确的是( )A、四边相等的四边形是菱形 B、一组对边相等,另一组对边平行的四边形是菱形 C、对角线互相垂直的四边形是菱形 D、对角线互相平分的四边形是菱形6. 甲、乙、丙、丁四人进行射击测试,每人测试 次,平均成绩均为 环,方差如下表:
选手
甲
乙
丙
丁
方差
则在这四个选手中,成绩最稳定的是( )
A、甲 B、乙 C、丙 D、丁7. 如果代数式 有意义,那么 的取值范围是( )A、 B、 C、 D、 且8. 如图,在水塔 的东北方向 处有一抽水站 在水塔的东南方 处有一建筑工地 在 间建一条直水管,则水管的长为( ) A、 B、 C、 D、9. 如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( )
A、 B、 C、 D、9. 如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是( ) A、 B、6 C、4 D、510. 若b>0,则一次函数y=﹣x+b的图象大致是( )A、
A、 B、6 C、4 D、510. 若b>0,则一次函数y=﹣x+b的图象大致是( )A、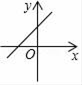 B、
B、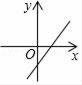 C、
C、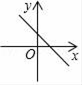 D、
D、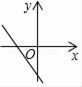 11. 甲、乙两地相距80km,一辆汽车上午9:00从甲地出发驶往乙地,匀速行驶了一半的路程后将速度提高了20km/h,并继续匀速行驶至乙地,汽车行驶的路程y(km)与时间x(h)之间的函数关系如图所示,该车到达乙地的时间是当天上午( )
11. 甲、乙两地相距80km,一辆汽车上午9:00从甲地出发驶往乙地,匀速行驶了一半的路程后将速度提高了20km/h,并继续匀速行驶至乙地,汽车行驶的路程y(km)与时间x(h)之间的函数关系如图所示,该车到达乙地的时间是当天上午( ) A、10:35 B、10:40 C、10:45 D、10:5012. 正方形的对角线长为 则它的两条对角线的交点到它的一边的距离为( )A、 B、 C、 D、
A、10:35 B、10:40 C、10:45 D、10:5012. 正方形的对角线长为 则它的两条对角线的交点到它的一边的距离为( )A、 B、 C、 D、二、填空题
-
13. 数据 的平均数是 则 是.14. 若实数a、b满足 ,则 = .15. 如图,直线l过正方形ABCD的顶点B,点A,C到直线l的距离分别是1和2,则正方形的边长是.
 16. 如图,已知函数y=2x+b与函数y=kx-3的图象交于点P(4,-6),则不等式kx-3>2x+b的解集是.
16. 如图,已知函数y=2x+b与函数y=kx-3的图象交于点P(4,-6),则不等式kx-3>2x+b的解集是.
三、解答题
-
17. 计算(1)、(2)、18. 如图,四边形ABCD中,AB=AD=2,BC=3,CD=1,∠A=90°,请问△BCD是直角三角形吗?请说明你的理由.
 19. 已知一次函数的图象经过A(-2,-3),B(1,3)两点.(1)、求这个一次函数的解析式;(2)、试判断点P(-1,1)是否在这个一次函数的图象上(3)、求此函数与x轴、y轴围成的三角形的面积.20. 2020年是特殊的一年,新年以来我们经历了新型冠状病毒肺炎,举国上下众志成城,共同抗疫.严酷战疫中,我们又一次感受到祖国的强大.口罩也成为人们防护防疫的必备武器.临高县某药店有 枚口罩准备出售.从中随机抽取了一部分口罩,根据它们的价格(单位:元),绘制出如下的统计图.请根据相关信息,解答下列问题:
19. 已知一次函数的图象经过A(-2,-3),B(1,3)两点.(1)、求这个一次函数的解析式;(2)、试判断点P(-1,1)是否在这个一次函数的图象上(3)、求此函数与x轴、y轴围成的三角形的面积.20. 2020年是特殊的一年,新年以来我们经历了新型冠状病毒肺炎,举国上下众志成城,共同抗疫.严酷战疫中,我们又一次感受到祖国的强大.口罩也成为人们防护防疫的必备武器.临高县某药店有 枚口罩准备出售.从中随机抽取了一部分口罩,根据它们的价格(单位:元),绘制出如下的统计图.请根据相关信息,解答下列问题: (1)、图 中 的值为 ;(2)、统计的这组数据的平均数为众数为 , 中位数为(3)、根据样本数据,估计这 枚口罩中,价格为 元的约有为枚.
(1)、图 中 的值为 ;(2)、统计的这组数据的平均数为众数为 , 中位数为(3)、根据样本数据,估计这 枚口罩中,价格为 元的约有为枚.

