贵州省铜仁市石阡县2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2021-07-23 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,点P(1,-2)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列汉字或字母中既是中心对称图形又是轴对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 3. 不等式组 的解集在数轴上表示为( )A、
3. 不等式组 的解集在数轴上表示为( )A、 B、
B、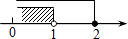 C、
C、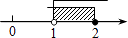 D、
D、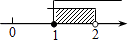 4. 下列命题中,错误的是( ).A、平行四边形的对角线互相平分 B、菱形的对角线互相垂直平分 C、矩形的对角线相等且互相垂直平分 D、角平分线上的点到角两边的距离相等5. 下列几组数中,能作为直角三角形三边长度的是( )A、2,3,4 B、4,5,6 C、6,8,11 D、5,12,136. 矩形的对角线长为20,两邻边之比为3:4,则矩形的面积为( )A、56 B、192 C、20 D、以上答案都不对7. 点P(-2,3)关于x轴的对称点的坐标是( )A、(-2,-3) B、(2,3) C、(-2,3) D、(-3,2)8. 若分式
4. 下列命题中,错误的是( ).A、平行四边形的对角线互相平分 B、菱形的对角线互相垂直平分 C、矩形的对角线相等且互相垂直平分 D、角平分线上的点到角两边的距离相等5. 下列几组数中,能作为直角三角形三边长度的是( )A、2,3,4 B、4,5,6 C、6,8,11 D、5,12,136. 矩形的对角线长为20,两邻边之比为3:4,则矩形的面积为( )A、56 B、192 C、20 D、以上答案都不对7. 点P(-2,3)关于x轴的对称点的坐标是( )A、(-2,-3) B、(2,3) C、(-2,3) D、(-3,2)8. 若分式 有意义,则x的取值范围是( ) A、x>3 B、x<3 C、x≠3 D、x=39. 若等腰三角形两边的长分别为3cm和7cm,则该三角形周长是( )A、13 B、17 C、13或17 D、2010. 如图所示,如果将一副三角板按如图方式叠放,那么 ∠1 等于( )
有意义,则x的取值范围是( ) A、x>3 B、x<3 C、x≠3 D、x=39. 若等腰三角形两边的长分别为3cm和7cm,则该三角形周长是( )A、13 B、17 C、13或17 D、2010. 如图所示,如果将一副三角板按如图方式叠放,那么 ∠1 等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图所示,小明从坡角为30°的斜坡的山底(A)到山顶(B)共走了50米,则山坡的高度BC为米.
 12. 如图,在四边形ABCD中,已知AB=CD,再添加一个条件(写出一个即可,图形中不再添加助线),则四边形ABCD是平行四边形.
12. 如图,在四边形ABCD中,已知AB=CD,再添加一个条件(写出一个即可,图形中不再添加助线),则四边形ABCD是平行四边形.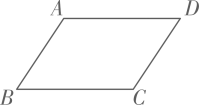 13. 函数 中自变量x的取值范围是 .14. 已知△ABC≌△DEF,且△ABC的三边长分别为3,4,5,则△DEF的周长为 cm.15. 菱形的周长是20,一条对角线的长为6,则它的面积为 .16. 如图,在△ABC中,BC的垂直平分线ED交AB于点E,交BC于点D,连接CE.如果△AEC的周长为12,AC=5,那么AB的长为.
13. 函数 中自变量x的取值范围是 .14. 已知△ABC≌△DEF,且△ABC的三边长分别为3,4,5,则△DEF的周长为 cm.15. 菱形的周长是20,一条对角线的长为6,则它的面积为 .16. 如图,在△ABC中,BC的垂直平分线ED交AB于点E,交BC于点D,连接CE.如果△AEC的周长为12,AC=5,那么AB的长为. 17. 若正多边形的一个内角等于140°,则这个正多边形的边数是 .18. 如图,将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,……如此继续下去,结果如下表:则an=(用含n的代数式表示).
17. 若正多边形的一个内角等于140°,则这个正多边形的边数是 .18. 如图,将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,……如此继续下去,结果如下表:则an=(用含n的代数式表示).
所剪次数
1
2
3
4
…
n
正三角形个数
4
7
10
13
…
an
三、解答题
-
19. 如图,在△ABC中,CE,BF是两条高,若∠A=70°,∠BCE=30°,求∠EBF与∠FBC的度数.
 20. 设矩形的一条对角线长为2cm,两条对角线组成的对顶角中,有一组是120°,求矩形的周长.21. 为创建“国家园林城市”,某校举行了以“爱我黄石”为主题的图片制作比赛,评委会对200名同学的参赛作品打分发现,参赛者的成绩x均满足50≤x<100,并制作了频数分布直方图,如图.
20. 设矩形的一条对角线长为2cm,两条对角线组成的对顶角中,有一组是120°,求矩形的周长.21. 为创建“国家园林城市”,某校举行了以“爱我黄石”为主题的图片制作比赛,评委会对200名同学的参赛作品打分发现,参赛者的成绩x均满足50≤x<100,并制作了频数分布直方图,如图.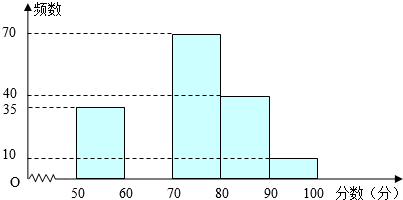
根据以上信息,解答下列问题:
(1)、请补全频数分布直方图;(2)、若依据成绩,采取分层抽样的方法,从参赛同学中抽40人参加图片制作比赛总结大会,则从成绩80≤x<90的选手中应抽多少人?(3)、比赛共设一、二、三等奖,若只有25%的参赛同学能拿到一等奖,则一等奖的分数线是多少?22. 如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行多少米? 23. 如图,在平行四边形ABCD中,E、F分别在AD、BC边上,且AE=CF.
23. 如图,在平行四边形ABCD中,E、F分别在AD、BC边上,且AE=CF.
求证:
(1)、△ABE≌△CDF;(2)、四边形BFDE是平行四边形.24. 如图,在菱形ABCD中,AC,BD相交于点O,E为AB的中点,DE⊥AB. (1)、求∠ABC的度数;(2)、若AC=43,求DE的长.25. 如图,在Rt ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动.同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)、求∠ABC的度数;(2)、若AC=43,求DE的长.25. 如图,在Rt ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动.同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF. (1)、求证:AE=DF;(2)、四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;(3)、当t为何值时, DEF为直角三角形?请说明理由.
(1)、求证:AE=DF;(2)、四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;(3)、当t为何值时, DEF为直角三角形?请说明理由.