浙江省温州市苍南县2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-07-22 类型:期末考试
一、选择题(本题有10小题,每小题3分,共30分。)
-
1. 下列图标属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 五边形的内角和为( )A、180° B、360° C、540° D、720°3. 下列选项中,计算正确的是( )A、 B、 C、 D、4. 测试五位学生的“一分钟跳绳”成绩,得到五个各不相同的数据,统计时,出现了一处错误:将最高成绩写得更高了,则其中不受影响的统计量是( )A、方差 B、标准差 C、中位数 D、平均数5. 若关于x的一元二次方程x2-2x+m=0有两个相等的实数根,则m的值是( )A、1 B、-1 C、4 D、-46. 如图,矩形ABCD中,对角线AC与BD相交于点O,AE⊥BD于点E,若∠BAE=2∠OAE,则∠AOB的度数为( )
2. 五边形的内角和为( )A、180° B、360° C、540° D、720°3. 下列选项中,计算正确的是( )A、 B、 C、 D、4. 测试五位学生的“一分钟跳绳”成绩,得到五个各不相同的数据,统计时,出现了一处错误:将最高成绩写得更高了,则其中不受影响的统计量是( )A、方差 B、标准差 C、中位数 D、平均数5. 若关于x的一元二次方程x2-2x+m=0有两个相等的实数根,则m的值是( )A、1 B、-1 C、4 D、-46. 如图,矩形ABCD中,对角线AC与BD相交于点O,AE⊥BD于点E,若∠BAE=2∠OAE,则∠AOB的度数为( ) A、18° B、54° C、70° D、72°7. 某口罩厂六月份的口罩产量为100万只,由于市场需求量增加,八月份的产量增长到144万只。已知该厂七、八月份的口罩产量的月平均增长率为x,则可列方程( )A、100(1+x)2=144 B、100(1-x)2=144 C、144(1+x)2=100 D、100(1+x)+100(1+x)2=1448. 如图,在正方形ABCD中,点E,F分别在边AD,CD上,且AE=DF,AF,BE交于点G。若 ,则 的值为( )
A、18° B、54° C、70° D、72°7. 某口罩厂六月份的口罩产量为100万只,由于市场需求量增加,八月份的产量增长到144万只。已知该厂七、八月份的口罩产量的月平均增长率为x,则可列方程( )A、100(1+x)2=144 B、100(1-x)2=144 C、144(1+x)2=100 D、100(1+x)+100(1+x)2=1448. 如图,在正方形ABCD中,点E,F分别在边AD,CD上,且AE=DF,AF,BE交于点G。若 ,则 的值为( ) A、 B、 C、 D、9. 已知反比例函数y= ,当-4≤x≤m时,n≤y≤n+3,则m的值是( )A、-2 B、-1 C、2 D、110. 如图,由两个全等菱形(菱形ABCD与菱形EFGH)组成的“四叶草”图案,其重叠部分是正八边形(阴影部分),点B,D在EG上,点F,H在AC上,若CF=2,则BD的长为( )
A、 B、 C、 D、9. 已知反比例函数y= ,当-4≤x≤m时,n≤y≤n+3,则m的值是( )A、-2 B、-1 C、2 D、110. 如图,由两个全等菱形(菱形ABCD与菱形EFGH)组成的“四叶草”图案,其重叠部分是正八边形(阴影部分),点B,D在EG上,点F,H在AC上,若CF=2,则BD的长为( ) A、4 B、2 C、2 D、2
A、4 B、2 C、2 D、2二、填空题(本题有8小题,每小题3分,共24分)
-
11. 二次根式 中字母x的取值范围是。12. 若反比例函数y= 的图象落在第二、四象限,则常数a的值可为。13. 在 ABCD中,∠A+∠C=100°,则∠B=度。14. 数据3,3,4,4,6的方差等于。15. 若关于x的一元二次方程ax2+2x-3=0的其中一个根是1,则另一个根是。16. 如图,将矩形ABCD沿对角线AC折叠,使点B落在点E处,CE与AD交于点F。若AF=5,DF=4,则AC的长为。
 17. 如图,在平面直角坐标系中,O为坐标原点,矩形OABC的顶点A,C分别在x轴,y轴的正半轴上,延长BC交反比例函数y1= 的图象于点E。若反比例函数y2= 的图象经过OB的中点D,且OB=OE,则k的值为。
17. 如图,在平面直角坐标系中,O为坐标原点,矩形OABC的顶点A,C分别在x轴,y轴的正半轴上,延长BC交反比例函数y1= 的图象于点E。若反比例函数y2= 的图象经过OB的中点D,且OB=OE,则k的值为。 18. 如图,在△CDE中,CD=1,∠CDE=45°,分别以CD,CE为边向外作正方形ABCD, CEFG。若AE=BD,则EF2=。
18. 如图,在△CDE中,CD=1,∠CDE=45°,分别以CD,CE为边向外作正方形ABCD, CEFG。若AE=BD,则EF2=。
三、解答题(本题有6小题,共46分)
-
19.(1)、计算:(2)、解方程: (x-1)2-4=020. 已知在学校组织的“一人一箭,古风重现"趣味竞赛中,每班参加射箭比赛的人数相同,学校将八年级一班和二班的射箭环数情况整理如下表:
射中环数(环)
6
7
8
9
10
一班(人)
7
5
4
1
3
二班(人)
4
8
m
n
1
(1)、八年-班射箭平均成绩是环(2)、若八年二班射箭平均成绩与八年一班相等①表中m,n的值分别为:m= ▲ ,n= ▲
②从两个班的平均数、中位数和众数等角度进行分析,你认为哪个班的整体成绩更好?
21. 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫格点,顶点在格点的四边形称为格点四边形.已知A,B,P均为格点,请在给定的网格中按要求画出格点平行四边形,且点P不与其它顶点重合。 (1)、在图甲中画一个以AB为边,且其邻边经过点P的平行四边形ABCD。(2)、在图乙中画一个以AB为对角线,且另一条对角线经过点P的平行四边形AEBF。22. 如图,点A (m,1)和点B在反比例函数y= (k>0,x>0)的图象上,过点A作AC∥y轴交x轴于点C,过点B作BD∥x轴交直线AC于点D,CD=3AC。
(1)、在图甲中画一个以AB为边,且其邻边经过点P的平行四边形ABCD。(2)、在图乙中画一个以AB为对角线,且另一条对角线经过点P的平行四边形AEBF。22. 如图,点A (m,1)和点B在反比例函数y= (k>0,x>0)的图象上,过点A作AC∥y轴交x轴于点C,过点B作BD∥x轴交直线AC于点D,CD=3AC。 (1)、若AD=BD,求k的值。(2)、连结OB,若四边形OBDC的面积为6,求点B的坐标。23. 用总长700cm的木板制作矩形置物架ABCD (如图),已知该置物架上面部分为正方形ABFE,下面部分是两个全等的矩形DGMN和矩形CNMH,中间部分为矩形EFHG。已知DG=60cm,设正方形的边长AB=x (cm)。
(1)、若AD=BD,求k的值。(2)、连结OB,若四边形OBDC的面积为6,求点B的坐标。23. 用总长700cm的木板制作矩形置物架ABCD (如图),已知该置物架上面部分为正方形ABFE,下面部分是两个全等的矩形DGMN和矩形CNMH,中间部分为矩形EFHG。已知DG=60cm,设正方形的边长AB=x (cm)。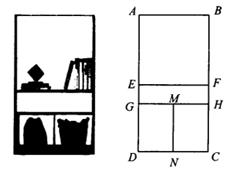 (1)、当x=75时,EG的长为cm(2)、置物架ABCD的高AD的长为cm (用含x的代数式表示)(3)、为了便于置放物品,EG的高度不小于26cm,若矩形ABCD的面积为12750 (cm2),求x的值。24. 在直角坐标系xOy中,四边形ABCD是矩形,点A在x轴上,点C在y轴的正半轴上,点B,D分别在第一,二象限,且AB=3,BC=4。
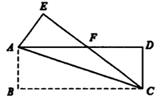
(1)、当x=75时,EG的长为cm(2)、置物架ABCD的高AD的长为cm (用含x的代数式表示)(3)、为了便于置放物品,EG的高度不小于26cm,若矩形ABCD的面积为12750 (cm2),求x的值。24. 在直角坐标系xOy中,四边形ABCD是矩形,点A在x轴上,点C在y轴的正半轴上,点B,D分别在第一,二象限,且AB=3,BC=4。 (1)、如图1,延长CD交x轴负半轴于点E,若AC=AE。
(1)、如图1,延长CD交x轴负半轴于点E,若AC=AE。①求证:四边形ABDE为平行四边形。
②求点A的坐标。
(2)、如图2,F为AB上一点,G为AD的中点,若点G恰好落在y轴上,且CG平分∠DCF,求AF的长。(3)、如图3,x轴负半轴上的点P与点Q关于直线AD对称,且AP=AD,若OBCQ的面积为矩形ABCD面积的 ,则BQ的长可为(写出所有可能的答案)。