浙江省丽水市2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-07-22 类型：期末考试

进入出卷网下载

一、选择题(本题有10小题，每小题3分，共30分。)

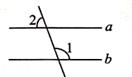
1. 计算2^-1的正确结果是（）

A、2 B、-2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 新冠疫苗载体腺病毒的直径约为0.000085毫米，将数0.000085用科学记数法表示为（）

A、85×10^-6 B、8.5×10^-5 C、8.5×10^-6 D、0.85×10^-4

查看试题解析
3. 如图，下列各角与∠A是同位角的是（）

A、∠1 B、∠2 C、∠3 D、∠4

查看试题解析
4. 某校要调查七、八、九三个年级1200名学生的睡眠情况，下列抽样选取最合适的是（）

A、选取该校100名七年级的学生 B、选取该校100名男生 C、选取该校100名女生 D、随机选取该校100名学生

查看试题解析
5. 下列多项式中，能用平方差公式分解因式的是（）

A、a²-1 B、-a²-1 C、a²+1 D、a²+a

查看试题解析
6. 已知 ${\begin{cases} x = 2 \\ y = 1 \end{cases}$ 是方程ax-y=3的解，则a的值为（）

A、2 B、1 C、5 D、 $\frac{1}{2}$

查看试题解析
7. 分式 $\frac{a + 0.2 b}{0.5 a - b}$ 变形正确的是（）

A、 $\frac{a + 2 b}{5 a - b}$ B、 $\frac{5 a + b}{a - 2 b}$ C、 $\frac{10 a + 2 b}{5 a - 10 b}$ D、 $- \frac{10 a + 2 b}{b - 5 a}$

查看试题解析
8. 已知10^x=m，10^y=n，则10^2x+3y等于（）

A、2m+3n B、m²+n³ C、6mn D、m²n³

查看试题解析
9. 为了改善生态环境，某社区计划在荒坡上种植600棵树，由于学生志愿者的加入，每日比原计划多种20%，结果提前1天完成任务．设原计划每天种树x棵，可列方程（）

A、 $\frac{600}{(1 + 20 %) x} - \frac{600}{x} = 1$ B、 $\frac{600}{x} - \frac{600}{(1 - 20 %) x} = 1$ C、 $\frac{600}{(1 - 20 %) x} - \frac{600}{x} = 1$ D、 $\frac{600}{x} - \frac{600}{(1 + 20 %) x} = 1$

查看试题解析
10. 如图，在△ABC中，∠ABC=50°，∠ACB=100°，点M是射线AB上的一个动点，过点M作MN∥BC交射线AC于点N，连结BN。若△BMN中有两个角相等，则∠MNB的度数不可能是（）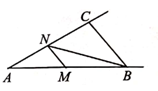

A、25° B、30° C、50° D、65°

查看试题解析

二、填空题(本题有6小题，每小题3分，共18分)

11. 因式分解：a²+2a+1= ．

查看试题解析
12. 如图，已知a∥b，∠1=110°，则∠2的度数是

查看试题解析
13. 数学小组对收集到的160个数据进行整理，绘制成扇形统计图。若某组数据的频数为40，则表示这组数据的扇形的圆心角度数是。

查看试题解析
14. 若关于x的方程 $\frac{m x + 1}{x^{2} - x} + \frac{2}{x - 1} = 0$ 有增根，则m的值是。

查看试题解析
15. 数学活动课上，小明同学尝试将正方形纸片剪去一个小正方形，剩余部分沿虚线剪开，拼成新的图形。现给出下列3种不同的剪、拼方案，其中能够验证平方差公式的方案是。(请填上正确的序号)

查看试题解析
16. 已知关于x，y的二元一次方程组 ${\begin{cases} x + y = a + b - 6 \\ x - y = a - b + 6 \end{cases}$ (a，b为实数)。

(1)、若x=2a-1，则a的值是；

(2)、若x，y同时满足ax+by+4=0，2x+5y-ay=0，则a+b的值是。

查看试题解析

三、解答题(本题有8小题，共52分)

17.

(1)、计算： b²·(b²)³

(2)、化简：a(a+2)-(a-2)(a+2)

查看试题解析
18. 用消元法解方程组 ${\begin{cases} x - 2 y = 7 ① \\ 3 x - 2 y = 5 ② \end{cases}$ 时，两位同学采用不同方法，部分过程如下：
方法一：由①-②，得：2x=2，

方法二：由②，得2x+(x-2y)=5，③

把①代入③，得2x+7=5，

(1)、观察上述两个消元过程，若有误，请在方框内打“×”，若正确，则打“√”

(2)、请用你喜欢的方法，求出此方程组的解．

查看试题解析
19. 先化简，再求值： $\frac{x^{2}}{x - 2} + \frac{4}{2 - x}$ ，其中x= $- \frac{9}{2}$

查看试题解析
20. 如图，在7×7的正方形网格中，线段AB的两个端点A，B在格点上，根据要求画出端点都在格点上的一条线段。

(1)、在图1中画出与AB相等的线段CD；

(2)、在图2中画出与AB平行的最长线段EF。

查看试题解析

21. 教育部印发的《大中小学劳动教育指导纲要(试行》指出，初中学生要承担一定的家庭劳动。为了解学生每周在家的劳动次数，某校随机抽取了部分学生进行调查，并利用抽样所得的数据绘制如下图表。请结合图表解决问题：

某校学生在家劳动情况统计表

劳动（次/周）	A（7次及以上）	B（5~6次）	C（3~4次）	D（2次及以下）
人数	20	a	90	32

某校学生在家劳动情况统计图

(1)、求参与本次调查的学生人数；

(2)、求出图表中a，b的值；

(3)、若该校共有学生10，请估计有多少学生每周在家劳动的次数为5次及以上？

查看试题解析

22. 如图，在△ABC中，CD⊥AB于点D，EF⊥CD于点G，∠ADE=∠EFC。

(1)、请说明∠B=∠EFC的理由；

(2)、若∠A=60°，∠ACB=72°，求∠CDE的度数。

查看试题解析
23. 某校举办七年级数学素养大赛，比赛共设三个项目：速算比赛、数学推理、巧解方程，每个项目得分都按一定百分比折算后计入总分。甲、乙、丙三位同学的速算比赛得分均为85分，且此项在总分中所占百分比不变，其余两项得分如下图所示(单位：分)。

(1)、根据图中信息判断哪位同学总分得分最低？

(2)、甲、丙两同学的数学推理与巧解方程两项经折算后的得分和均为52分，求这两项在计入总分时所占的百分比；

(3)、写出三个项目各项所占百分比的一组值，使甲或丙同学能获得第一名。

查看试题解析
24. 如图，在长方形ABCD中，AB=10，BC=9，点E在AB上，点G在AD上，AEFG为正方形。点M，N分别为BC，CD上的动点，MO⊥BC，NO⊥CD，且点O始终在正方形AEFG的内部，MO交EF于点P，NO交FG于点Q。

(1)、设CM=AE=a，
①用含a的代数式表示四边形EBMP的周长；

②若四边形OPFQ，GQND的周长之和恰好为四边形EBMP周长的两倍，求a的值。

(2)、设CM=3x，CN=2x，AE=nCN，是否存在正整数x，n，使得S_{四边形EBMF}=S_{四边形GQND}？若存在，求出x，n的值；若不存在，请说明理由。

查看试题解析