浙江省丽水市2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期：2021-07-22 类型：期末考试
一、选择题(本题有10小题，每小题3分，共30分。)
-
1. 在下列方程中，属于一元二次方程的是（ ）。A、3x-4=0 B、x2-3x=0 C、x+3y=2 D、 =32. 下列图形中，既是中心对称图形又是轴对称图形的是（ ）A、平行四边形
B、等边三角形 
C、矩形 
D、正五边形 
3. 一组数据：11，12，14，12，13，则这组数据的中位数是（ ）A、11 B、12 C、13 D、144. 如图，在矩形ABCD中，对角线AC，BD相交于点O，AC=10，∠ACB=30°，则CD的长为（ ）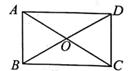
A、5 B、10 C、5 D、55. 若反比例函数y= (k≠0)的图象经过点(2，3)，则该图象必经过点（ ）A、(1，6) B、(-2，3) C、(2，-3) D、(-6，1)6. 假设命题“a>0"不成立，那么a与0的大小关系只能是（ ）A、a≠0 B、a≤0 C、a=0 D、a<07. 如图，在四边形ABCD中，对角线AC，BD相交于点O，且OA=OC，OB=OD，下列结论不一定成立的是（ ）
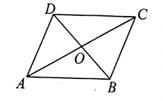A、AB∥DC B、AD=BC C、∠ABC=∠ADC D、∠DBC=∠BAC8. 用配方法将方程x2-6x=1转化为(x+a)2=b的形式，则a，b的值分别为（ ）A、a=3，b=1 B、a=-3，b=1 C、a=3，b=10 D、a=-3，b=109. 设实数 的整数部分为a，小数部分为b，则b2+2ab的值为（ ）A、1 B、 -5 C、3 D、-310. 如图，正方形ABCD的边长为a，P是对角线AC上的点，连结PB，过点P作PQ⊥BP交线段CD于点Q。当DQ=2CQ时，BP的长为（ ）
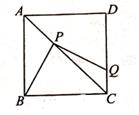A、 B、 C、 D、二、填空题(本题有6小题，每小题3分，共18分)
-
11. 二次根式 中字母x的取值范围为。12. 如图，在 ABCD中，∠A=130°，则与∠BCD相邻的外角∠DCE的度数为。
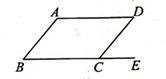13. 若一元二次方程的二次项系数为1，常数项为0，它的一个根为2，则该方程为。14. 如图，在Rt△ABC中，∠ACB=90°，D，E，F分别是边AB，AC，BC的中点。若CD的长为3，则EF的长是 。
15. 如图，在平面直角坐标系中，菱形ABCD的顶点A与原点O重合，点C在直线y=x_上，点B的坐标为(2，1)将菱形ABCD沿直线y=x平移，当点B，D同时落在反比例函数y= (x>0)的图象上时，菱形沿直线y=x平移的距离为。
16. 已知二次多项式x2-ax+a-5(1)、当x=1时，该多项式的值为；(2)、若关于x的方程x2-ax+a-5=0，有两个不相等的整数根，则正数a的值为。三、解答题(本题有8小题，共52分)
-
17. 计算(1)、(2)、18. 解方程(1)、7x2=28(2)、x2+3x=019. 已知点A(3，m)在反比例函数y= 的图象上(1)、求m的值；：(2)、当3<x<6时，求y的取值范围．．20. 某果园实验基地种植了相同数量的甲、乙两个品种西瓜，为了分析哪个品种更适宜推广，随机从甲、乙两个品种中各采摘5个西瓜，测得西瓜的质量(kg) (均取整数)，绘制成如下折线统计图。
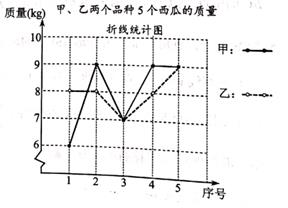(1)、请你分别求出甲、乙两个品种所选的5个西瓜的平均质量；(2)、已知 =1.6(kg)， =0.4(kg)。根据己有的统计量，并结合折线统计图，你认为哪个品种更适宜推广？请简述理由。21. 如图在 ABCD中， E，F是对角线BD上的两点，AE⊥BD于点E，CF⊥BD于点F。
(1)、求证：△ABE≌△CDF；(2)、若BE=2，BD=5，求EF的长。22. 如图，斜靠在墙上的一根竹竿AB的长为10米，竹竿底端到墙的距离BC为6米。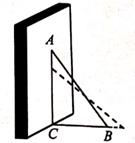
(1)、求竹竿顶端到地面距离AC的长：(2)、若A端沿着垂直于地面的方向AC下移a米(a>0)，B端沿CB方向恰好也移动了a米，求a的值。23. 如图，已知直线OA与反比例函数y= (x>0)，y= (x>0)的图象分别交于点A，B，点A的坐标为(1，4)，且点B是线段OA的中点。
(1)、求k1 ， k2的值；(2)、已知反比例函数y= 的图象上C点的横坐标为2，连结OC并延长交反比例函数y= 的图象于点D，连结AD，BC，试判断AD与BC的数量关系和位置关系，请说明理由。24. 如图，在菱形ABCD中，∠BAD=120°，线段AE与AB重合，以AE为边向右侧作正三角形AEF，△AEF绕点A按逆时针方向旋转，旋转角∠BAE=α(0°<α<60°)，射线BE，DF交于点G，连结CE，CG，CF。
(1)、求证：BE=CF；(2)、求∠BGD的度数；(3)、当△ECG为等腰三角形时，求 的值。