浙江省温州市乐清市2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期：2021-07-22 类型：期末考试
一、选择题（本题有10个小题，每小题3分，共30分）
-
1. 要使二次根式 有意义，则x的取值范围是（ ）A、x≥1 B、x>1 C、x≥-1 D、x>-12. 下列各式中，能与 合并的是（ ）A、 B、 C、 D、3. 下列图形中，是中心对称图形的是（ ）A、
B、
C、
D、
4. 在平面直角坐标系中，点A（2，-3）在反比例函数y= 的图象上，下列各点在此反比例函数图象上的是（ ）A、P（-2，3） B、Q（-2，-3） C、S（1，6） D、T（4，-2）5. 将80辆环保电动汽车一次充电后行驶里程记录数据，获得如图所示条形统计图，根据统计图所测数据的中位数、众数分别是（ ）
A、165，160 B、165，165 C、170，165 D、160，1656. 已知关于x的一元二次方程x2-4x+m=0有两个相等的实数根，则m值是（ ）A、0 B、1 C、2 D、47. 用反证法证明命题“如果a∥b，c∥b，那么a∥c时，应假设（ ）A、a⊥c B、c不平行b C、a不平行b D、a不平行c8. 如图，菱形ABCD中，AB=13，AC=10，则BD的长度为（ ）
A、24 B、16 C、12 D、89. 已知点（-1，y1），（-3，y2），（3，y3）在函数y= 的图象上，则（ ）A、y1<y2<y3 B、y2<y1<y3 C、y3<y1<y2 D、y3<y2<y110. 已知关于x的方程x2-7x+6a=0的一个解是x1=2a，则原方程的另一个解是（ ）A、x2=0或7 B、x2=3或4 C、x2=3或7 D、x2=4或7二、填空题（本题有8个小题，每小题3分，共24分）
-
11. 当x= 时， 值为0。12. 若使平行四边形ABCD为矩形，需添加一个条件为。（填出一种情况即可）13. 如图，在五边形ABCDE中，∠D=120°，与∠EAB相邻的外角是80°，与∠DEA，∠ABC相邻的外角都是60°，则∠C为度。
14. 一艘快艇的航线如图所示，从O港出发，1小时后到达A地，若快艇的行驶速度保持不变，则快艇驶完AB这段路程的时间为小时。
15. 如图，已知点P是正方形ABCD对角线BD上一点，且AP=3，PF⊥CD于点F，PE⊥BC于点E，连结EF，则EF的长为 。
16. 如图，O是等边三角形ABC内任意一点，过点O作OD∥AB，OE∥AC，OF∥BC分别交AC，BC，AB于点G，H，I，已知等边三角形ABC的周长18，则OD+OE+OF= 。
17. 如图，点A在反比例函数y= （x>0）的图象上，作AB⊥y轴，AC⊥x轴分别交反比例函数y= （x>0）图象于点B，C，点C在点A的下方，连结BC，若△ABC的面积为 ，则k的值为。
18. 小李家大门上的矩形装饰物由金属丝焊接而成，该图形既是轴对称图形又是中心对称图形，如图，在矩形ABCD中，两个菱形由平行于AD的固定条固定，EF，IJ是中间的固定条，上下固定条都经过菱形各边中点，且所有固定条不经过菱形内部。已知F，M，G分别到AB，BC，AD的距离都是2cm，若对角线FH=AB= FG，顶点H，K之间距离是EF的2倍，则金属丝总长（即图中所有线段之和）是cm。
三、解答题（本题有5小题，共46分。解答时需要写出必要的文字说明、演算步骤或证明过程）
-
19.(1)、计算：(2)、解方程：x2-2x-1=020. 如图，在7×7网格中，
线段AB的两个端点和点C都在网格的格点上，分别按下列要求仅用无刻度直尺画图（保留作图痕迹）。
(1)、在图甲中画线段AB的中点M。(2)、在图乙中画线段CD，使得CD= AB21. 如图，小强同学根据乐清市某天上午和下午各四个整点时间的气温绘制成的折线统计图。
(1)、根据图中信息分别求出上午和下午四个整点时间的平均气温。(2)、请你根据所学统计学知识，从四个整点时间温度猜测，这天上午和下午的气温哪个更稳定，并说明理由。22. 学校的学生专用智能饮水机在工作过程：先进水加满，再加热至100℃时自动停止加热，进入冷却期，水温降至25℃时自动加热，水温升至100℃又自动停止加热，进入冷却期，此为一个循环加热周期，在不重新加入水的情况下，一直如此循环工作。如图，表示从加热阶段的某一时刻开始计时，时间为x（分）与对应的水温为y（℃）函数图象关系，已知AB段为线段，BC段为双曲线一部分，点A为（0，28），点B为（9，100），点C为（a，25）。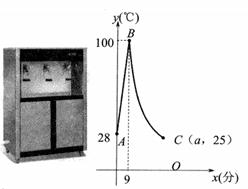
(1)、求出AB段加热过程的y与x的函数关系式和a的值。(2)、若水温y（℃）在45≤y≤100时为不适饮水温度，在0≤x≤a内，在不重新加入水的情况下，不适饮水温度的持续时间为多少分？23. 如图，正方形ABCD中，E，F，G分别是CD，AD，AB上的中点，连结BE，BF，AE，连结CG分别交BE，BF于点M，N，AE交BF于点H。
(1)、求证：AE∥CG(2)、当点P从点A匀速运动到点E时，点Q恰好从点C匀速运动到点N处，若AB=10，设CQ=4t。①求AH的长。
②当AP>AH时，用含t代数式表示四边形QNHP的面积。
③在P，Q整个运动过程中，当P，Q与四边形MNHE的两个顶点构成平行四边形时，求t的值。