四川省雅安市2021年中考数学试卷
试卷更新日期:2021-07-22 类型:中考真卷
一、单选题
-
1. -2021的绝对值等于( )A、2021 B、-2021 C、 D、2. 我国在2020年10月开展了第七次人口普查,普查数据显示,我国2020年总人口达到14.1亿( ).A、 B、 C、 D、3. 在平面直角坐标系中,点 关于y轴的对称点的坐标是( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 若 的值为零,则x的值为( )A、-1 B、1 C、 D、06. 如图,在 中, ,点F为AC中点, 是 的中位线,若 ,则BF=( )
 A、6 B、4 C、3 D、57. 甲和乙两个几何体都是由大小相同的小立方块搭成,它们的俯视图如图,小正方形中数字表示该位置上的小立方块个数( )
A、6 B、4 C、3 D、57. 甲和乙两个几何体都是由大小相同的小立方块搭成,它们的俯视图如图,小正方形中数字表示该位置上的小立方块个数( )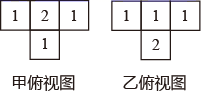 A、甲和乙左视图相同,主视图相同 B、甲和乙左视图不相同,主视图不相同 C、甲和乙左视图相同,主视图不相同 D、甲和乙左视图不相同,主视图相同8. 下列说法正确的是( )A、一个不透明的口袋中有3个白球和2个红球(每个球除颜色外都相同),则从中任意摸出一个球是红球的概率为 B、一个抽奖活动的中奖概率为 ,则抽奖2次就必有1次中奖 C、统计甲,乙两名同学在若干次检测中的数学成绩发现: , ,说明甲的数学成绩比乙的数学成绩稳定 D、要了解一个班有多少同学知道“杂交水稻之父”袁隆平的事迹,宜采用普查的调查方式9. 若直角三角形的两边长分别是方程 的两根,则该直角三角形的面积是( )A、6 B、12 C、12或 D、6或10. 如图,将 沿 边向右平移得到 , 交 于点G.若 . .则 的值为( )
A、甲和乙左视图相同,主视图相同 B、甲和乙左视图不相同,主视图不相同 C、甲和乙左视图相同,主视图不相同 D、甲和乙左视图不相同,主视图相同8. 下列说法正确的是( )A、一个不透明的口袋中有3个白球和2个红球(每个球除颜色外都相同),则从中任意摸出一个球是红球的概率为 B、一个抽奖活动的中奖概率为 ,则抽奖2次就必有1次中奖 C、统计甲,乙两名同学在若干次检测中的数学成绩发现: , ,说明甲的数学成绩比乙的数学成绩稳定 D、要了解一个班有多少同学知道“杂交水稻之父”袁隆平的事迹,宜采用普查的调查方式9. 若直角三角形的两边长分别是方程 的两根,则该直角三角形的面积是( )A、6 B、12 C、12或 D、6或10. 如图,将 沿 边向右平移得到 , 交 于点G.若 . .则 的值为( ) A、2 B、4 C、6 D、811. 如图,四边形 为⊙的内接四边形,若四边形为菱形, 为( ).
A、2 B、4 C、6 D、811. 如图,四边形 为⊙的内接四边形,若四边形为菱形, 为( ). A、45° B、60° C、72° D、36°12. 定义: ,若函数 ,则该函数的最大值为( )A、0 B、2 C、3 D、4
A、45° B、60° C、72° D、36°12. 定义: ,若函数 ,则该函数的最大值为( )A、0 B、2 C、3 D、4二、填空题
-
13. 从-1, ,2中任取两个不同的数作积,则所得积的中位数是.14. 已知一元二次方程 的两根分别为m,n,则 的值为.15. 如图, 为正六边形, 为正方形,连接CG,则∠BCG+∠BGC=.
 16. 若关于x的分式方程 的解是正数,则k的取值范围是.17. 如图,在矩形 中, 和 相交于点O,过点B作 于点M,交 于点F,过点D作DE∥BF交AC于点N.交AB于点E,连接 , .有下列结论:①四边形 为平行四边形,② ;③ 为等边三角形;④当 时,四边形DEBF是菱形.正确结论的序号.
16. 若关于x的分式方程 的解是正数,则k的取值范围是.17. 如图,在矩形 中, 和 相交于点O,过点B作 于点M,交 于点F,过点D作DE∥BF交AC于点N.交AB于点E,连接 , .有下列结论:①四边形 为平行四边形,② ;③ 为等边三角形;④当 时,四边形DEBF是菱形.正确结论的序号.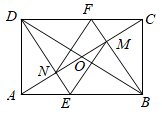
三、解答题
-
18.(1)、计算:(2)、先化简,再求值: ,其中 .19. 为庆祝中国共产党成立100周年,某中学组织全校学生参加党史知识竞赛,从中任取20名学生的竞赛成绩进行统计.

组别
成绩范围
频数
A
60~70
2
B
70~80
m
C
80~90
9
D
90~100
n
(1)、分别求m,n的值;(2)、若把每组中各学生的成绩用这组数据的中间值代替(如60~70的中间值为65)估计全校学生的平均成绩;(3)、从A组和D组的学生中随机抽取2名学生,用树状图或列表法求这2名学生都在D组的概率.20. 某药店选购了一批消毒液,进价为每瓶10元,在销售过程中发现销售量y(瓶)与每瓶售价x(元)之间存在一次函数关系(其中 ,且x为整数),当每瓶消毒液售价为12元时,每天销售量为90瓶;当每瓶消毒液售价为15元时,每天销售量为75瓶;(1)、求y与x之间的函数关系式;(2)、设该药店销售该消毒液每天的销售利润为w元,当每瓶消毒液售价为多少元时,药店销售该消毒液每天销售利润最大.21. 如图, 为等腰直角三角形,延长 至点B使 ,其对角线 , 交于点E. (1)、求证: ;(2)、求 的值.22. 已知反比例函数 的图象经过点 .
(1)、求证: ;(2)、求 的值.22. 已知反比例函数 的图象经过点 .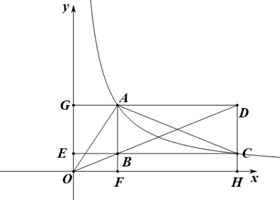 (1)、求该反比例函数的表达式;(2)、如图,在反比例函数 的图象上点A的右侧取点C,作CH⊥x轴于H,过点A作y轴的垂线AG交直线 于点D.
(1)、求该反比例函数的表达式;(2)、如图,在反比例函数 的图象上点A的右侧取点C,作CH⊥x轴于H,过点A作y轴的垂线AG交直线 于点D.①过点A,点C分别作x轴,y轴的垂线,交于B,垂足分别为为F、E,连结OB,BD,求证:O,B,D三点共线;
②若 ,求证: .
23. 如图,在⊙ 中, 是直径, ,垂足为P,过点 的 的切线与 的延长线交于点 , 连接 .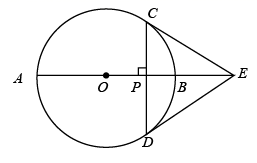 (1)、求证: 为⊙ 的切线;(2)、若⊙ 半径为3, ,求 .24. 已知二次函数 .
(1)、求证: 为⊙ 的切线;(2)、若⊙ 半径为3, ,求 .24. 已知二次函数 .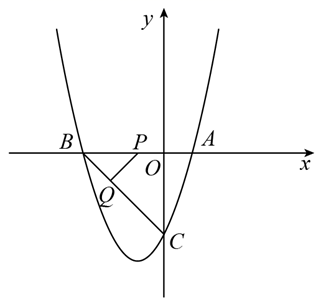 (1)、当该二次函数的图象经过点 时,求该二次函数的表达式;(2)、在(1) 的条件下,二次函数图象与x轴的另一个交点为点B,与y轴的交点为点C,点P从点A出发在线段AB上以每秒2个单位长度的速度向点B运动,同时点Q从点B出发,在线段BC上以每秒1个单位长度的速度向点C运动,直到其中一点到达终点时,两点停止运动,求△BPQ面积的最大值;(3)、若对满足 的任意实数x,都使得 成立,求实数b的取值范围.
(1)、当该二次函数的图象经过点 时,求该二次函数的表达式;(2)、在(1) 的条件下,二次函数图象与x轴的另一个交点为点B,与y轴的交点为点C,点P从点A出发在线段AB上以每秒2个单位长度的速度向点B运动,同时点Q从点B出发,在线段BC上以每秒1个单位长度的速度向点C运动,直到其中一点到达终点时,两点停止运动,求△BPQ面积的最大值;(3)、若对满足 的任意实数x,都使得 成立,求实数b的取值范围.