重庆市九龙坡区2020-2021学年七年级下学期数学期末考试试卷

试卷更新日期：2021-07-22 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个数中，无理数是（）

A、0.2 B、 $\sqrt[3]{27}$ C、 $\sqrt{64}$ D、 $3 π$

查看试题解析
2. 下列的调查中，选取的样本最具有代表性的是（）

A、为了解九龙坡区居民的防火意识，对该地区的初中生进行调查 B、为了解万象城某专卖店的平均营业额，选在周末进行调查 C、为了解某校1500名学生的视力情况，随机抽取该校150名学生进行调查 D、为了解全校学生课外小组的活动情况，对该校的女生进行调查

查看试题解析
3. 如图，点 $E$ 在 $B C$ 的延长线上，下列条件不能判断 $A B / / C D$ 的是（）

A、 $∠ 1 = ∠ 2$ B、 $∠ 3 = ∠ 4$ C、∠5=∠B D、 $∠ B + ∠ B C D = 180 °$

查看试题解析
4. 如图，数轴上点A表示的数最有可能是（）

A、 $\sqrt{3}$ B、 $\sqrt{5}$ C、 $\sqrt{7}$ D、 $\sqrt{10}$

查看试题解析
5. $\sqrt{81}$ 的算术平方根是（）

A、9 B、±9 C、3 D、±3

查看试题解析
6. 若将点A（－1，3）向右平移2个单位，再向下平移4个单位得到点B，则点B在第（）象限

A、一 B、二 C、三 D、四

查看试题解析
7. 新冠疫情得到有效控制后，妈妈去药店为即将开学的小明和已经复工的爸色购买口罩.若买40只一次性医用口罩和20只KN95口罩，需付380元；若买50只一次性医用口罩和30只KN95口罩，需付550元.设一只一次性医用口罩x元，一只KN9S5口罩y元，下面所列方程组正确的是（）

A、 ${\begin{array}{l} 40 x + 20 y = 550 \\ 50 x + 30 y = 380 \end{array}$ B、 ${\begin{array}{l} 40 x + 20 y = 380 \\ 50 x + 30 y = 550 \end{array}$ C、 ${\begin{array}{l} 40 x + 20 y = 380 \\ 50 y + 30 x = 550 \end{array}$ D、 ${\begin{array}{l} 50 x + 20 y = 380 \\ 40 x + 30 y = 550 \end{array}$

查看试题解析
8. 下列图形都是由同样大小的圆按一定的规律组成，其中第1个图形中有5个圆，第2个图形中有9个圆，第3个图形中有14个圆，...则第8个图形中圆的个数是（）

A、52 B、53 C、54 D、55

查看试题解析
9. 下列命题：①如果一个数的立方根等于这个数的本身，那么这个数一定是0和1；②过直线外一点有且只有一条直线与已知直线平行；③若 $(m^{2} - 1) a < (m^{2} - 1) b$ ，则 $a < b$ ；④两条直线被第三条直线所截，同位角相等.其中假命题是（）

A、①② B、②③ C、①③ D、①③④

查看试题解析
10. 若关于x、y的方程组 ${\begin{array}{l} 2 x + 3 y = 3 \\ a x - b y = - 5 \end{array}$ 和 ${\begin{array}{l} 3 x - 2 y = 11 \\ b x - a y = 1 \end{array}$ 有相同的解，则 ${(a + b)}^{2021}$ 的值为（）

A、 $- 1$ B、0 C、1 D、2021

查看试题解析
11. 在数轴上，若A、B两点对应的实数分别是－2和 $\sqrt{11}$ 点B是A、C两点的中点，则点C所对应的实数是（）

A、 $\sqrt{13} + 2$ B、 $\sqrt{11} + 4$ C、 $2 \sqrt{11} + 2$ D、 $2 \sqrt{26} - 2$

查看试题解析
12. 已知关于x、y的二元一次方程组 ${\begin{array}{l} x - 4 y = 0 \\ a x + 4 y = 16 \end{array}$ 的解为整数，且关于x的不等式组 ${\begin{array}{l} x \geq - 2 \\ x < \frac{2 - a}{4} \end{array}$ 恰有3个整数解，则所有满足条件的整数a的和为（）

A、－1 B、－2 C、－6 D、－8

查看试题解析

二、填空题

13. 计算： $| \sqrt{5} - 5 | - \sqrt{25} =$

查看试题解析
14. 已知点A（ $4 a - 3$ ， $a + 1$ ）在x轴上，则a＝

查看试题解析
15. 如图，将一副三角尺按如图所示方式摆放，点A，B， D在同一条直线上，EF∥AD，∠E＝60°，则∠BFD的度数为度

查看试题解析
16. 若 $a > b$ ，则 $- 3 a + 1$ $- 3 b + 1$ （用“＜”或“＞”填空）

查看试题解析
17. 如图，在直角△ABC中，∠BAC＝90°，AB＝6，AC＝8，BC＝10，∠ABC的平分线交AC于点D，点E、F分别是BD、AB上的动点，则AE＋EF的最小值为

查看试题解析
18. 如图，在长方形ABCD中，点E在AD上，连接BE、CE.将△ABE沿BE翻折得到△A′BE，△DCE 沿CE翻折得到△D'CE，分别作∠CED、∠A′BC的角平分线相交于点F.若∠BCE＝40°，∠A′ED′＝m°，则∠BFE的度数为度（用含m的代数式表示）.

查看试题解析

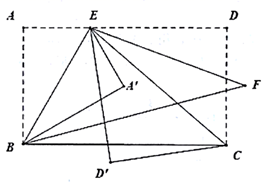
三、解答题

19. 解方程组：

(1)、 ${\begin{array}{l} x - y = 3 \\ 3 x + y = 13 \end{array}$

(2)、 ${\begin{array}{l} \frac{2}{3} x - \frac{1}{4} y = \frac{3}{2} \\ 2 (x - y) - 3 (2 x + y) = 17 \end{array}$

查看试题解析
20.

(1)、解关于x的不等式 $12 - 5 (4 x - 3) \geq 4 (1 - 3 x)$ ，并求出其最大整数解；

(2)、解关于x的不等式组 ${\begin{array}{l} 4 (x - 1) + 3 \geq 5 (1 - 2 x) \\ \frac{x - 1}{2} > \frac{2 x + 4}{3} \end{array}$

查看试题解析
21. 如图，点F在线段AB上，点E、G在线段CD上，FG∥AE，∠1＝∠2

(1)、求证：AB∥CD；

(2)、若FG⊥BC于点H，BC平分∠ABD，∠A＝50°，求∠D的度数

查看试题解析
22. 为了解学生掌握垃圾分类知识的情况，增强学生环保意识，某校举行了“垃圾分类人人有责"的知识竞赛活动.现随机抽取部分同学的成绩x （单位：分）进行统计，下面给出了部分信息
a.被抽取的部分同学成绩的频数分布直方图和扇形统计图如图所示，且成绩从低到高划分为A、B、C、D、E五组，其对应的数据分别是：50≤x＜60，60≤x＜70，70≤x＜80，80≤x＜90，90≤x≤100；

b.划分在D组的成绩分数具体是：80，80，81，82，83，83，84，84，85，85，86，87，88，89，89

根据以上信息，完成下列问题：

(1)、本次调查中，一共抽取了名同学的成绩；

(2)、扇形图中，a＝，扇形A的圆心角度数为度；

(3)、把频数分布直方图补充完整；

(4)、如果全校有2000名学生参加这次活动，85 分以上（含85 分）为优秀，那么估计获得优秀奖的学生有多少人？

查看试题解析
23. 平面直角坐标系xOy中△ABC的三个顶点分别是A（－3，－4），B（2，－1），C（－1，1）

(1)、在所给的网格图中，画出这个平面直角坐标系：

(2)、点A经过平移后对应点为 $A_{1}$ （－5，－1），将△ABC作同样的平移得到三角形△ $A_{1} B_{1} C_{1}$ ，画出平移后的△ $A_{1} B_{1} C_{1}$ ，井分别写出点 $B_{1}$ ， $C_{1}$ 的坐标；

(3)、设点 $P$ 在y轴上，且△ $P B_{1} C_{1}$ 的面积与△ $A_{1} B_{1} C_{1}$ 的面积相等，求点P的坐标

查看试题解析
24. 阅读材料：材料一：对三个实数x、y、z，规定 $\min {x ， y ， z}$ 表示x、y、z这三个数中最小的数，例如min{－1，2，3}＝－1
材料二：m、n都是实数，且满足2m＝n＋8，则称点P（ $m - 1$ ， $\frac{n + 2}{2}$ ）为“开心点”

例：点A（5，3），由 ${\begin{array}{l} m - 1 = 5 \\ \frac{n + 2}{2} = 3 \end{array}$ ，则 ${\begin{array}{l} m = 6 \\ n = 4 \end{array}$ ，∵2×6＝4＋8，∴点A是“开心点”；

又例：点B（4，8），由 ${\begin{array}{l} m - 1 = 4 \\ \frac{n + 2}{2} = 8 \end{array}$ ，则 ${\begin{array}{l} m = 5 \\ n = 14 \end{array}$ ，∵2×5≠14＋8，∴点B不是“开心点”.

请解决下列问题：

(1)、min{ $- \sqrt{3} ， - \sqrt{5} ， - π$ }＝；

(2)、若点T（ $t + 3$ ， $3 t - 1$ ）是“开心点”，请求点T的坐标；

(3)、若整数a满足min ${4 ， \frac{5 a + 2}{3} ， 11 - 2 a}$ ＝4，请判断点M（a，1）是否为“开心点”，并说明理由

查看试题解析
25. 现阶段直播带货和“网红经济”正迅速发展，某水果店主老张紧跟时代潮流，在抖音上直播卖水果第一次直播期间，卖出奉节脐橙礼盒装75盒，眉山耙耙柑礼盒装30盒，一共收入5850元.第二次直播期间，卖出奉节脐橙礼盒装100盒，眉山耙耙柑礼盒装50盒，一共收入 8500元.第一次直播和第二次直播期间奉节脐橙和眉山耙耙柑每盒的价格没有变化.

(1)、求奉节脐橙和眉山耙耙柑每盒的价格分别是多少元？

(2)、为了回馈顾客，在第三次直播期间，奉节脐橙每盒降价m%，眉山耙耙柑每盒降价 $\frac{5}{7}$ m%，于是奉节脐橙的销量在第二次直播的基础上增加了25%，眉山耙耙柑的销量在第二次直播的基础上增加了30%.若此次直播总销售额在第一次直播的总销售额基础上至少增加3050元，求m的最大值

查看试题解析
26. 已知点B、D分别为射线AM、AN上异于端点A的任一点，点C为∠MAN内部一点（如图1）.∠A＝ $α$ ，∠C＝ $β$ ，（0°＜ $α$ ＜180°，0°＜ $β$ ＜180°）

(1)、∠ABC＋∠ADC＝（用含 $α$ 、 $β$ 的代数式直接填空）；

(2)、如图2，若 $α = β$ ＝90°，BE平分∠ABC，DG平分∠CDN，若射线BE与DG所在直线交于点F，则∠BDG为角（只填序号）；①锐角：②直角；③钝角

(3)、①若∠MBC、∠CDN的角平分线相交于点P， $α + β =$ 110°， ∠BPD＝30°，试求 $α$ 、 $β$ 的值；
②①中的∠BPD是否一定存在？若∠BPD不存在，请直接写出 $α$ 、 $β$ 满足的条件

查看试题解析