江苏省泰州市高港区2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-07-22 类型:期末考试
一、单选题
-
1. 下列图形中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列调查中,适宜采用普查的是( )A、调查全国初中生的视力情况 B、疫情复学后调查进校学生的体温情况 C、调查某品牌汽车的抗撞击情况 D、调查泰州市市民2020年人均收入情况3. 下列与 相等的分式是( )A、 B、 C、 D、4. 如图,在同一直角坐标系中,一次函数y=kx+3与反比例函数 的图象位置可能是( )A、
2. 下列调查中,适宜采用普查的是( )A、调查全国初中生的视力情况 B、疫情复学后调查进校学生的体温情况 C、调查某品牌汽车的抗撞击情况 D、调查泰州市市民2020年人均收入情况3. 下列与 相等的分式是( )A、 B、 C、 D、4. 如图,在同一直角坐标系中,一次函数y=kx+3与反比例函数 的图象位置可能是( )A、 B、
B、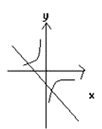 C、
C、 D、
D、 5. 关于x的方程 的解是正数,则a的取值范围是( )A、a>-1 B、a>-1且a≠0 C、a<-1 D、a<-1且a≠-26. 如图,在正方形ABCD中,AD=10,点E,F是正方形ABCD内的两点,且AE=FC=6,BE=DF=8,则EF的长为( )
5. 关于x的方程 的解是正数,则a的取值范围是( )A、a>-1 B、a>-1且a≠0 C、a<-1 D、a<-1且a≠-26. 如图,在正方形ABCD中,AD=10,点E,F是正方形ABCD内的两点,且AE=FC=6,BE=DF=8,则EF的长为( )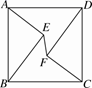 A、2 B、4 C、 D、2
A、2 B、4 C、 D、2二、填空题
-
7. 若二次根式 有意义,则x的取值范围是 .8. 为了解我区各社区新冠疫情防控工作开展的情观,需对相关信息进行调查统计,请运用所学统计如识,对下列统计的主要步骤进行合理的排序(只填序号):①利用统计图表对数据加以表示;②在各个社区随机抽取部分居民发放《社区疫情防控工作调查问卷》,调查相关信息;③分析并作出判断;④对收集的数据信息加以整理.9. 若分式 的值为0,则x的取值是.10. 如图,矩形ABCD的对角线交于点O,若 , ,则BC的长为.
 11. 若 与最简二次根式 能合并成一项,则 .12. 如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是
11. 若 与最简二次根式 能合并成一项,则 .12. 如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是
13. 我国古代数学名著《算法统宗)有一道“荡秋干”的问题,“平地秋千未起,踏板一尺离地.送行二步与人齐,5尺人高曾记,仕女家人争蹴.良工高士素好奇,算出索长有几?”此问题可理解为:如图,有一架秋千,当它静止时,踏板离地距离PA的长为1尺,将它向前水平推送10尺时,即 尺,秋千踏板离地的距离 就和身高5尺的人一样高,秋千的绳索始终拉得很直,则秋千的绳索长为尺. 14. 若一元二次方程 有两个实数根,则m的取值范围是.15. 如图,在下列网格中,每一个小正方形的边长为1,请在网格中找出一点D,使四边形ABCD为平行四边形,则平行四边形ABCD边AB上的高的长度为.
14. 若一元二次方程 有两个实数根,则m的取值范围是.15. 如图,在下列网格中,每一个小正方形的边长为1,请在网格中找出一点D,使四边形ABCD为平行四边形,则平行四边形ABCD边AB上的高的长度为. 16. 如图,在平面直角坐标系中,△ABO的边AB平行于y轴,反比例函数y= (x>0)的图象经过OA中点C和点B,且△OAB的面积为6,则k=.
16. 如图,在平面直角坐标系中,△ABO的边AB平行于y轴,反比例函数y= (x>0)的图象经过OA中点C和点B,且△OAB的面积为6,则k=.
三、解答题
-
17. 计算(1)、(2)、18. 先化简,再求值: ,其中x满足 .19. 已知关于x的一元二次方程 .(1)、求证:此方程有两个不相等的实数根;(2)、设此方程的两个根分别为 , ,若 ,求方程的两个根.20. 一个不透明的袋中装有2个白球,3个红球,每个球除颜色外都相同,将球摇匀.(1)、①从中任意摸出1个球是黑球;②从中任意摸出1个球是白球;③从中任意摸出1个球是红球;④从中任意摸出3个球,其中有红球.
上述事件是随机事件的是 , 是确定事件的是(只填序号).将它们的序号按发生的可能性从小到大的顺序排列为.
(2)、现往袋中放入黑、白两种球共4个,每个球与袋中的球除颜色外都相同,将球摇匀,此时从中任意摸出1个球,摸到三种颜色的球的概率都相等,则放入的黑球个数为 , 白球的个数为.21. 人口普查能全面摸清人口数量、结构、分布等方面的情况,2020年我国进行了七次人口普查,本次普查为推动我国经济高质量发展、建设现代化经济体系提供了强有力的支撑.下面的统计图呈现了我国人口普查的部分情况.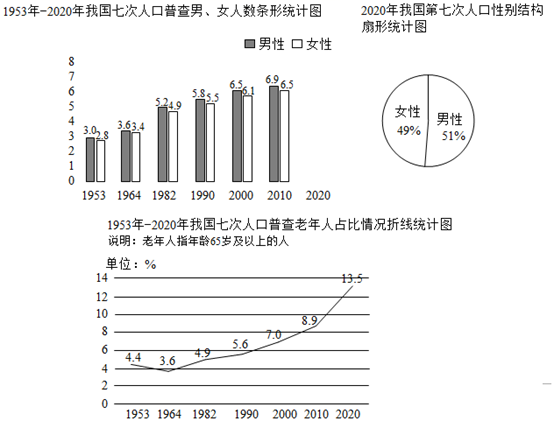
根据上面统计图的信息,解决下列问题:
(1)、2010年第六次人口普查总人口约为亿人;2020年第七次人口普查与2010年第六次人口普查相比,总人口数增长了5.2%,则2020年第七次人口普查总人口数约为亿人,其中65岁及以上人口约为亿人.(结果均保留一位小数)(2)、总人口性别比是指“总人数中男性人口数与女性人口数的比”,则2020年第七次人口普查总人口性别比约为.(结果保留两位小数)(3)、下列作出的判断错误的一个是(只填序号)①我国总人口数不断上升,人口增长速度也呈上升趋势;
②我国人口老龄化程度进一步加深:
③近10年我国总人口性别比略微下降,性别结构情况相对稳定.
22. 泰州市某工程队准备修建一条长3000米的盲道,由于采用新的施工方式,实际每天修建盲道的长度比原计划多.给出下列信息:①实际每天修建盲道的长度比原计划增加25%;②提前2天完成这一任务;③原计划每天修建的长度比实际修建长度少75米.
请在上述三条信息中选择其中两条作为条件,你选择的条件是 (只填序号),并根据选择的条件求出原计划每天修建盲道多少米?
23. 有两根长度均为l的铁丝,将这两根铁丝分别围成一个长方形(长和宽不等)和正方形,设长方形的长为x.(1)、长方形的面积为 , 正方形的面积为.(用含x、l的代数式表示)(2)、试比较长方形与正方形面积的大小,并说明理由.24. 如图,已知等腰 中, ,E为BD边上的中点,过点D作 ,且 ,连接BC.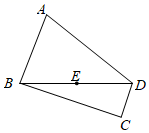 (1)、请仅用无刻度的直尺在图中,画出 的AB边上的高线DF,写出作法,并证明 .(2)、若四边形ABCD的面积为12,设 , ,请判断x、y是否存在函数关系?若存在,请求出它们的函数关系式,若不存在,请说明理由.25. 请根据学习函数的经验,将下列探究函数 图象与性质的过程补充完整:(1)、函数 的自变量x的取值范围是;(2)、下表列出了y与x的几组对应值,请写出其中m、n的值; , ;
(1)、请仅用无刻度的直尺在图中,画出 的AB边上的高线DF,写出作法,并证明 .(2)、若四边形ABCD的面积为12,设 , ,请判断x、y是否存在函数关系?若存在,请求出它们的函数关系式,若不存在,请说明理由.25. 请根据学习函数的经验,将下列探究函数 图象与性质的过程补充完整:(1)、函数 的自变量x的取值范围是;(2)、下表列出了y与x的几组对应值,请写出其中m、n的值; , ;…
0
2
3
4
…
…
2
1
…
(3)、在如图所示的平面直角坐标系中,描全上表中以各对对应值为坐标的点,并面出该函数的图象. (4)、结合函数的图象,写出该函数的一条性质:(5)、根据图象直接写出 时x的取值范围:26.
(4)、结合函数的图象,写出该函数的一条性质:(5)、根据图象直接写出 时x的取值范围:26.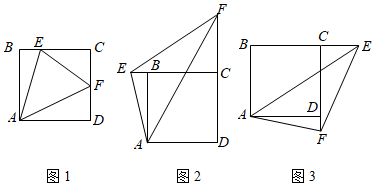 (1)、(发现证明)
(1)、(发现证明)问题:如图1,在正方形ABCD中,点E、F分别是BC、CD边上的动点,且 ,求证: .
观察:EF、DF、BE三条线段都不在同一条直线上,能不能借助图形的运动,将部分线段放置在一条直线上加以证明呢?
思路:将 绕点A顺时针旋转90°使AB与AD重合,得到了旋转后的 .
①根据上述思路在图1中画图分析并证明(写出详细的证明过程).
②若正方形ABCD的边长为6,当动点E在BC边上运动到中点位置时,动点F在CD边上距离D点多长的位置?(写出详细的解答过程)
(2)、(类比迁移)若点E、F分别为正方形两条边的延长线上的动点,EF、BE、DF三者之间还存在(1)中的关系吗?根据解决(1)中问题的经验加以探究.
①如图2,在正方形ABCD中,点E、F分别是CB、DC延长线上的动点,且 ,EF、BE、DF之间的数量关系是什么?请借助图2加以分析,并写出详细的证明过程.
②如图3,在正方形ABCD中,点E、F分别是BC、CD延长线上的动点,且 ,则EF、BE、DF之间的数量关系是 ▲ (直接写出关系式,无需证明).