重庆市七校联盟2020-2021学年七年级上学期数学第一次月考试卷

试卷更新日期：2021-07-22 类型：月考试卷

进入出卷网下载

一、单选题

1. 我国古代数学著作《增删算法统宗》记载“绳索量竿”问题：“一条竿子一条索，索比竿子长一托.折回索子却量竿，却比竿子短一托.”其大意为：现有一根竿和一条绳索，用绳索去量竿，绳索比竿长5尺；如果将绳索对半折后再去量竿，就比竿短5尺.设绳索长x尺.则符合题意的方程是（）

A、 $\frac{1}{2} x = (x - 5) - 5$ B、 $\frac{1}{2} x = (x + 5) + 5$ C、 $2 x = (x - 5) - 5$ D、 $2 x = (x + 5) + 5$

查看试题解析
2. 如果a的相反数是2，那么a等于（）

A、 $- 2$ B、2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
3. 如图所示，数轴上相邻刻度间的线段表示一个单位长度，点A，B，C，D对应的数分别是a，b，c，d，且 $2 a + b + d = 0$ ，那么数轴的原点应是 $()$ .

A、点A B、点B C、点C D、点D

查看试题解析
4. 在 $△ ABC$ 中，a、b、c分别是 $∠ A$ ， $∠ B$ ， $∠ C$ 的对边，若 ${(a - \sqrt{5})}^{2} + | b + \sqrt[3]{- 8} | + \sqrt{c - 2} = 0$ ，则这个三角形一定是 $()$

A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、等边三角形

查看试题解析
5. 定义一种对正整数n的“F”运算：①当n为奇数时，结果为3n+5；②当n为偶数时，结果为 $\frac{n}{2^{k}}$ (其中k是使 $\frac{n}{2^{k}}$ 为奇数的正整数)，并且运算可以重复进行。例如，取n=26，则：

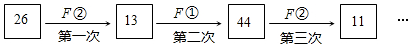
若n=49，则第449次“F运算”的结果是（）

A、98 B、88 C、78 D、68

查看试题解析
6. 设 $a - b = 2$ ， $a - c = \frac{1}{2}$ ，则整式 ${(c - b)}^{2} + 3 (b - c) + \frac{9}{4}$ 的值为 $($ $)$

A、 $\frac{9}{2}$ B、 $\frac{9}{4}$ C、9 D、0

查看试题解析
7. 要制作一个密封的长方体铁盒，嘉嘉设计出了它的三视图，如图，按图中尺寸（单位：cm）判断，要制作这个长方体铁盒，如果只考虑面积因素，采用下列哪种面积的铁板最合理（　　）

A、1000cm² B、1030cm² C、1100cm² D、1200cm²

查看试题解析
8. 下列说法中错误的是（　　）

A、一个锐角的补角一定是钝角 B、同角或等角的余角相等 C、两点间的距离是连结这两点的线段的长度 D、过直线l上的一点有且只有一条直线垂直于l

查看试题解析
9. 在 $△ A B C$ 中， $B C = 6$ ， $A C = 3$ ，过点C作 $C P ⊥ A B$ ，垂足为P，则CP长的最大值为 $()$

A、5 B、4 C、3 D、6

查看试题解析
10. 如图，直线 $A B$ 与直线CD交于点O， $E O ⊥ A B$ 于点O，则 $∠ 1$ 与 $∠ 2$ 的关系是（）

A、互为对顶角 B、相等 C、互补 D、互余

查看试题解析
11. 如图，已知直线 $A B$ 、 $C D$ 被直线 $A C$ 所截， $A B / / C D$ ，E是直线 $A C$ 右边任意一点（点E不在直线 $A B$ ， $C D$ 上），设 $∠ B A E = α$ ， $∠ D C E = β$ ．下列各式：① $α + β$ ，② $α - β$ ，③ $β - α$ ，④ $360 ° - α - β$ ， $∠ A E C$ 的度数可能是（）

A、①②③ B、①②④ C、①③④ D、①②③④

查看试题解析
12. 下列说法中不正确的个数有（）
①1是绝对值最小的有理数；

②若a²=b² ，则a³=b³；

③两个四次多项式的和一定是四次多项式；

④多项式x²﹣3kxy﹣3y²+ $\frac{1}{3}$ xy﹣8合并同类项后不含xy项，则k的值是 $\frac{1}{9}$ .

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 已知 $M$ ， $N$ 为数轴上从原点 $O$ 出发的两个动点，点 $M$ 每秒1个单位，点 $N$ 的速度为点 $M$ 的2倍，则当运动时间为4秒时， $O M$ 和 $O N$ 两条线段的中点相距个单位.

查看试题解析
14. 规定：用{m}表示大于m的最小整数，例如{ $\frac{5}{2}$ }＝3，{4}＝5，{﹣1.5}＝﹣1等；用[m]表示不大于m的最大整数，例如[ $\frac{7}{2}$ ]＝3，[2]＝2，[﹣3.2]＝﹣4，如果整数x满足关系式：3{x}+2[x]＝13，则x＝.

查看试题解析
15. 设 $P = x^{2} - 3 x y$ ， $Q = 3 x y - 9 y^{2}$ ，若 $P = Q$ ，则 $\frac{x}{y}$ 的值为.

查看试题解析
16. 如图所示是一种棱长分别是2cm，3cm，4cm的长方体积木，现要用若干块这样的积木来搭建大长方体，如果用6块积木来搭，那么搭成的大长方体的表面积最小是 ${cm}^{2}$ .

查看试题解析
17. 把时针从钟面数字“12”开始，按顺时针方向拨到“6”，记做拨了 $+ \frac{1}{2}$ 周，那么把时针从钟面数字“12”开始拨了 $- \frac{1}{4}$ 周，则该时针所指的钟面数字为.

查看试题解析
18. 观察下列图形：已知 $a ∥ b ，$ 在第一个图中，可得∠1+∠2=180°，则按照以上规律： $∠ 1 + ∠ 2 + ∠ P_{1} + \dots + ∠ P_{n} =$ 度.

查看试题解析

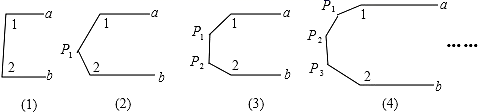
三、解答题

19. 计算

(1)、 $| - 3 | + {(- 1)}^{2014} \times {(π - 3.14)}^{0} - {(- \frac{1}{3})}^{- 2}$

(2)、 ${(2 x^{2} y)}^{3} \cdot (- 3 x y^{2}) \div (12 x^{4} y^{5})$

查看试题解析
20. 如图1，已知数轴上有三点A、B、C， $A B = B C$ ，点C对应的数是200，且 $B C = 300$ .

(1)、求A对应的数；

(2)、若动点P、Q分别从A、C两点同时出发向左运动，同时动点R从A点出发向右运动，当点Q、R相遇时，点P、Q、R即停止运动，已知点P、Q、R的速度分别为每秒10个单位长度、5个单位长度、2个单位长度，M为线段PR的中点，N为线段RQ的中点，问多少秒时恰好满足 $M R = 4 R N$ ？

(3)、若点E、D对应的数分别为 $- 800$ 、0，动点K、L分别从E、D两点同时出发向左运动，点K、L的速度分别为每秒10个单位长度、5个单位长度，点G为线段KL的中点，问：点L在从点D运动到点A的过程中， $\frac{3}{2} L C - A G$ 的值是否发生变化？若不变，求其值.若变化，请说明理由.

查看试题解析

21. 如图为一梯级平面图，一只老鼠沿长方形的两边

A - B - C

的路线逃跑，一只猫同时沿梯级

(

折线

) A - C - D

的路线追，结果在距离C点

0.6 m

的D点处，猫捉住了老鼠，已知老鼠的速度是猫的

\frac{11}{14}

，求梯级

(

折线

) A - C

的长度，

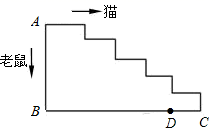(1)、请将下表中每一句话“译成”数学语言

(

在表格中写出对应的代数式

)

：

设梯级 $($ 折线 $) A \to C$ 的长度为	xm
$A B + B C$ 的长度为
$A \to C \to D$ 的长度为
$A \to B \to D$ 的长度为
设猫捉住老鼠所用时间为	ts
猫的速度是
老鼠的速度是

(2)、根据表格中代数式列出一个你认为正确的方程

(

不要求解

)

：.

查看试题解析

22. 如图，将一幅直角三角板的直角顶点C叠放在一起.

(1)、若 $∠ D C E = 33 °$ ，则 $∠ B C D =$ ；若 $∠ A C B = 138 °$ ，则 $∠ D C E =$ .

(2)、猜想 $∠ A C B$ 与 $∠ D C E$ 的大小有何特殊关系？并说明理由.

(3)、如图（2），若是两个同样的直角三角板 $60 °$ 锐角的顶点A重合在一起，则 $∠ D A B$ 与 $∠ C A E$ 的数量关系为.

查看试题解析
23. 生活中的易拉罐、电池、圆形的笔筒等都是一种叫做圆柱体的立体图形（如图1所示），当把它的上底面、下底面和侧面展开后发现上底面和下底面是两个大小相同的圆，侧面是一个长方形（如图2所示）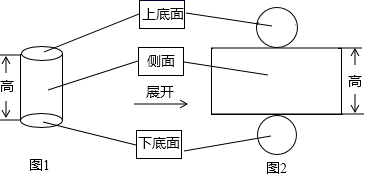

(1)、一个圆柱体的铝制易拉罐上、下两个底面的半径都是4cm，侧面高为15cm，制作这样一个易拉罐需要面积多大的铝材？ $($ 不计接缝 $)$ .

(2)、如果一个圆柱体的铝制装饰品的高是5cm，而且侧面的面积等于上、下两个底面面积之和，那么底面的半径是cm.

(3)、一张正方形的铝材边长是40cm，可单独用于制作 $(2)$ 题中铝制装饰品的侧面或单独用于制作底面，若要使制成的侧面和底面正好能成为一套完整的装饰品，那么制作侧面的铝材张数与制作底面的铝材张数之比为.

查看试题解析
24. 如图1，直角三角形DEF与直角三角形ABC的斜边在同一直线上，∠EDF＝30°，∠ABC＝40°，CD平分∠ACB，将△DEF绕点D按逆时针方向旋转，记∠ADF为α（0°＜α＜180°），在旋转过程中；

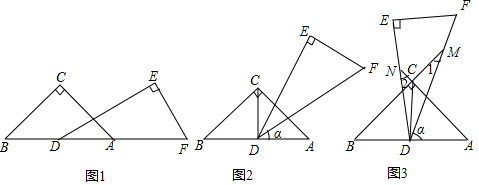(1)、如图2，当∠α＝时， $D E // B C$ ，当∠α＝时，DE⊥BC；

(2)、如图3，当顶点C在△DEF内部时，边DF、DE分别交BC、AC的延长线于点M、N，
①此时∠α的度数范围是 ▲ ；

②∠1与∠2度数的和是否变化？若不变求出∠1与∠2度数和；若变化，请说明理由；

③若使得∠2≥2∠1，求∠α的度数范围.

查看试题解析
25. 仔细阅读下列解题过程：
若 $a^{2} + 2 a b + 2 b^{2} - 6 b + 9 = 0$ ，求 $a 、 b$ 的值.

解： $∵ a^{2} + 2 a b + 2 b^{2} - 6 b + 9 = 0$

$\begin{array}{l} ∴ a^{2} + 2 a b + b^{2} + b^{2} - 6 b + 9 = 0 \\ ∴ {(a + b)}^{2} + {(b - 3)}^{2} = 0 \\ ∴ a + b = 0 ， b - 3 = 0 \\ ∴ a = - 3 ， b = 3 \end{array}$

根据以上解题过程，试探究下列问题：

(1)、已知 $x^{2} - 2 x y + 2 y^{2} - 2 y + 1 = 0$ ，求 $x + 2 y$ 的值；

(2)、已知 $a^{2} + 5 b^{2} - 4 a b - 2 b + 1 = 0$ ，求 $a 、 b$ 的值；

(3)、若 $m = n + 4 ， m n + t^{2} - 8 t + 20 = 0$ ，求 $n^{2 m}^{- t}$ 的值.

查看试题解析