重庆市七校联盟2020-2021学年八年级上学期数学第一次月考试卷
试卷更新日期:2021-07-22 类型:月考试卷
一、单选题
-
1. 在下列实数 , , , , 中无理数的个数有( )A、1个 B、2个 C、3个 D、4个2. 下列运算正确的是( )A、a﹣(b+c)=a﹣b+c B、2a2•3a3=6a5 C、a2+a2=2a4 D、(x﹣y)2=x2﹣y23. 如图是5×5的正方形方格图,点A,B在小方格的顶点上,要在小方格的顶点确定一点C,连接AC和BC,使△ABC是等腰三角形,则方格图中满足条件的点C的个数是( )
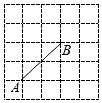 A、4 B、5 C、6 D、74. 定义:△ABC中,一个内角的度数为 ,另一个内角的度数为 ,若满足 ,则称这个三角形为“准直角三角形”.如图,在Rt△ABC中,∠C=90°, AC=8,BC=6,D是BC上的一个动点,连接AD,若△ABD是“准直角三角形”,则CD的长是( )
A、4 B、5 C、6 D、74. 定义:△ABC中,一个内角的度数为 ,另一个内角的度数为 ,若满足 ,则称这个三角形为“准直角三角形”.如图,在Rt△ABC中,∠C=90°, AC=8,BC=6,D是BC上的一个动点,连接AD,若△ABD是“准直角三角形”,则CD的长是( ) A、 B、 C、 D、5. 某商店根据今年6--10 月份的销售额情况,剩作了如下统计图.根据图中信息,可以判断相邻两个月销售额变化最大的是( )
A、 B、 C、 D、5. 某商店根据今年6--10 月份的销售额情况,剩作了如下统计图.根据图中信息,可以判断相邻两个月销售额变化最大的是( )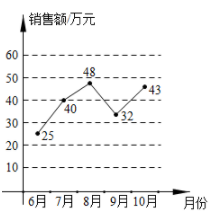 A、6月到7月 B、7月到8月 C、8月到9月 D、9月到10月6. 如图,在 中, 平分 , , ,则 的长为( )
A、6月到7月 B、7月到8月 C、8月到9月 D、9月到10月6. 如图,在 中, 平分 , , ,则 的长为( ) A、3 B、11 C、15 D、97. 一个自然数的算术平方根为 ,则与它相邻的下一个自然数的平方根是( )A、 B、 C、 D、8. 下列多项式中,不能进行因式分解的是( )A、﹣a2+b2 B、﹣a2﹣b2 C、a3﹣3a2+2a D、a2﹣2ab+b2﹣19. 如图,在 中, , 是 的平分线, , ,垂足分别是 、 .给出下列四个结论:
A、3 B、11 C、15 D、97. 一个自然数的算术平方根为 ,则与它相邻的下一个自然数的平方根是( )A、 B、 C、 D、8. 下列多项式中,不能进行因式分解的是( )A、﹣a2+b2 B、﹣a2﹣b2 C、a3﹣3a2+2a D、a2﹣2ab+b2﹣19. 如图,在 中, , 是 的平分线, , ,垂足分别是 、 .给出下列四个结论: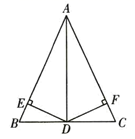
① 上任意一点到点 、 的距离相等;② 上任意一点到 、 的距离相等;③ , ;④ .其中正确的结论有( ).
A、1个 B、2个 C、3个 D、4个10. 在△ABC中,AB=10,BC=12,BC边上的中线AD=8,则△ABC边AB上的高为( )A、8 B、9.6 C、10 D、1211. 如图,在四边形ABCD中,AD=5,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为( ) A、 B、 C、 D、12. 已知实数m,n,p,q满足 , ,则 ( )A、48 B、36 C、96 D、无法计算
A、 B、 C、 D、12. 已知实数m,n,p,q满足 , ,则 ( )A、48 B、36 C、96 D、无法计算二、填空题
-
13. 若 + =0,则x+y=.14. 某校对学生上学方式进行了一次抽样调查,并根据此次调查结果绘制了一个不完整的扇形统计图,其中“其他”部分所对应的圆心角是36°,则“步行”部分所占百分比是 .
 15. 已知:关于x的二次三项式 是完全平方式,则常数k等于.16. 如图,Rt△ABC中,∠C=90°,AC=2,BC=5,点D是BC边上一点且CD=1,点P是线段DB上一动点,连接AP,以AP为斜边在AP的下方作等腰Rt△AOP.当P从点D出发运动至点B停止时,点O的运动路径长为 .
15. 已知:关于x的二次三项式 是完全平方式,则常数k等于.16. 如图,Rt△ABC中,∠C=90°,AC=2,BC=5,点D是BC边上一点且CD=1,点P是线段DB上一动点,连接AP,以AP为斜边在AP的下方作等腰Rt△AOP.当P从点D出发运动至点B停止时,点O的运动路径长为 .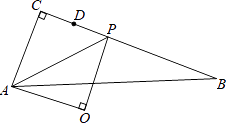 17. 如图,四边形ABCD中,AB=BC=3,∠A=∠C=90°,∠ABC=120°,点E是对角线BD上的一个动点,过点E分别作AB,BC,CD,AD的垂线,垂足分别为点F,H,I,G,连结FG和HI,则FG+HI的最小值为.
17. 如图,四边形ABCD中,AB=BC=3,∠A=∠C=90°,∠ABC=120°,点E是对角线BD上的一个动点,过点E分别作AB,BC,CD,AD的垂线,垂足分别为点F,H,I,G,连结FG和HI,则FG+HI的最小值为.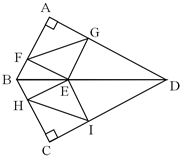 18. 一个长、宽分别为a、b的长方形的周长为10,面积为6,则 的值为.
18. 一个长、宽分别为a、b的长方形的周长为10,面积为6,则 的值为.三、解答题
-
19. 计算(1)、(2)、20. 阅读下列学习材料并解决问题
定义:如果一个数 的平方等于 记为 这个数 叫做虚数单位.它的加,减,乘法运算与整式的加,减,乘法运算类似.例如计算:
.
(1)、问题:填空: , .(2)、计算: ; ;(3)、试一试:请利用以前学习的有关知识将 化简成 的形式(即分母不含 的形式).21. 已知:如图,在△ABC中,AB>AC,∠B=45°,点D是BC边上一点,且AD=AC,过点C作CF⊥AD于点E,与AB交于点F. (1)、若∠CAD=α,求:
(1)、若∠CAD=α,求:①∠BCA的大小;
②∠BCF的大小;(用含α的式子表示)
(2)、求证:AC=FC.22. 某校的20年校庆举办了四个项目的比赛,现分别以A,B,C,D表示它们.要求每位同学必须参加且限报一项.以701班为样本进行统计,并将统计结果绘制如下两幅统计图,其中参加A项目的人数比参加C与D项目人数的总和多1人,参加D项目的人数比参加A项目的人数少11人.请你结合图中所给出的信息解答下列问题: (1)、求出全班总人数;(2)、求出扇形统计图中参加D项目比赛的学生所在的扇形圆心角的度数;(3)、若该校7年级学生共有200人,请你估计这次活动中参加A和B项目的学生共有多少人?23. 如果一个直角三角形的三边长分别为 ,a, , ,则称这个三角形为均匀直角三角形.
(1)、求出全班总人数;(2)、求出扇形统计图中参加D项目比赛的学生所在的扇形圆心角的度数;(3)、若该校7年级学生共有200人,请你估计这次活动中参加A和B项目的学生共有多少人?23. 如果一个直角三角形的三边长分别为 ,a, , ,则称这个三角形为均匀直角三角形. (1)、判定按照上述定义,下列长度的三条线段能组成均匀直角三角形的是( )
(1)、判定按照上述定义,下列长度的三条线段能组成均匀直角三角形的是( )A.1,2,3; , ,2;
, ,3; ,4,5.
(2)、性质求证:任何均匀直角三角形的较小直角边与较大直角边的比是3:4.(3)、应用如图,在一块均匀直角三角形纸板ABC中剪一个矩形,且矩形的一边在AB上,其余两个顶点分别在BC,AC上,已知 , , ,求剪出矩形面积的最大值.24. (1)、如图①,已知: 中, , ,直线m经过点A, 于D, 于E,求证: ;(2)、拓展:如图②,将(1)中的条件改为: 中, ,D、A、E三点都在直线m上,并且 , 为任意锐角或钝角,请问结论 是否成立?如成立,请证明;若不成立,请说明理由;(3)、应用:如图③,在 中, 是钝角, , , ,直线m与BC的延长线交于点F,若 , 的面积是12,求 与 的面积之和.25. 材料一:一个正整数x能写成x=a2﹣b2(a,b均为正整数,且a≠b),则称x为“雪松数”,a,b为x的一个平方差分解,在x的所有平方差分解中,若a2+b2最大,则称a,b为x的最佳平方差分解,此时F(x)=a2+b2 .
(1)、如图①,已知: 中, , ,直线m经过点A, 于D, 于E,求证: ;(2)、拓展:如图②,将(1)中的条件改为: 中, ,D、A、E三点都在直线m上,并且 , 为任意锐角或钝角,请问结论 是否成立?如成立,请证明;若不成立,请说明理由;(3)、应用:如图③,在 中, 是钝角, , , ,直线m与BC的延长线交于点F,若 , 的面积是12,求 与 的面积之和.25. 材料一:一个正整数x能写成x=a2﹣b2(a,b均为正整数,且a≠b),则称x为“雪松数”,a,b为x的一个平方差分解,在x的所有平方差分解中,若a2+b2最大,则称a,b为x的最佳平方差分解,此时F(x)=a2+b2 .例如:24=72﹣52 , 24为雪松数,7和5为24的一个平方差分解,32=92﹣72 , 32=62﹣22 , 因为92+72>62+22 , 所以9和7为32的最佳平方差分解,F(32)=92+72
材料二:若一个四位正整数,它的千位数字与个位数字相同,百位数字与十位数字相同,但四个数字不全相同,则称这个四位数为“南麓数”.例如4334,5665均为“南麓数”.
根据材料回答:
(1)、请直接写出两个雪松数,并分别写出它们的一对平方差分解;(2)、试证明10不是雪松数;(3)、若一个数t既是“雪松数”又是“南麓数”,并且另一个“南麓数”的前两位数字组成的两位数与后两位数字组成的两位数恰好是t的一个平方差分解,请求出所有满足条件的数t中F(t)的最大值.