四川省江油市八校2020-2021学年八年级上学期第一次月考数学试题
试卷更新日期：2021-07-22 类型：月考试卷
一、单选题
-
1. 下列每组数分别是三根木棒的长度不能用它们摆成三角形的是（ ）A、3cm，4cm，5cm B、8cm，7cm，15cm C、5cm，6cm，10cm D、5cm，8cm，12cm2. 若△ABC≌△DEF，△ABC的周长为100，AB=30，EF=25，则AC=（ ）A、55 B、45 C、30 D、253.
如图，OA＝OB，OC＝OD，∠O＝50°，∠D＝35°，则∠AEC等于（ ）
A、60° B、50° C、45° D、30°4. 如图，AB＝AC，BD⊥AC于D，CE⊥AB于E，BD、CE交于O，连结AO，则图中共有全等三角形的对数为（ ）
A、2对 B、3对 C、4对 D、5对5. 如图，AB∥DE，CD=BF，若要证明△ABC≌△EDF，还需补充的条件是（ ）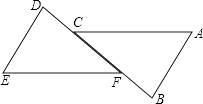
A、AC=EF B、AB=ED C、∠B=∠E D、不用补充6. 如图在△ABC中∠C=90°，AD平分∠BAC交BC于D，若BC=64，且BD：CD=9：7，则点D到AB边的距离为（ ）
A、18 B、32 C、28 D、247. 如图，CE是△ABC的外角∠ACD的平分线，若∠B=35°，∠ACE=60°，则∠A=（ ）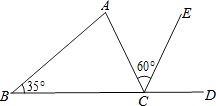
A、35° B、95° C、85° D、75°8. 若一个正n边形的每个内角为144°，则这个正n边形的所有对角线的条数是（ ）A、25 B、35 C、45 D、559. 若一个三角形的三条边长分别为3，2a+1，7，则整数a的值不可能是（ ）A、1 B、2 C、3 D、410. 已知△ABC中，∠A=20°，∠B=∠C，那么三角形△ABC是（ ）A、锐角三角形 B、直角三角形 C、钝角三角形 D、正三角形11. 已知△ABC中，∠ABC和∠ACB的平分线交于点O，则∠BOC一定（ ）A、小于直角 B、等于直角 C、大于直角 D、不能确定12. 如图，△ABC中，AE是∠BAC的角平分线，AD是BC边上的高线，且∠B=40°，∠C=70°，则∠EAD的度数（ ）
A、35° B、5° C、15° D、25°二、填空题
-
13. 如图，自行车的三角形支架利用的是三角形的 性.
14. 如图，一个直角三角形纸片，剪去直角后，得到一个四边形，则∠1+∠2= ．
15. 如图，在△ABC中，AB=8，AC=6，则BC边上的中线AD的取值范围是.
16. 如图，已知△ABC的周长是21，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD=3，△ABC的面积是 ．
17. 如图，AD是△ABC的角平分线，DE⊥AC，垂足为E，BF∥AC交ED的延长线于点F，若BC恰好平分∠ABF，AE＝2BF.给出下列四个结论：①DE＝DF；②DB＝DC；③AD⊥BC；④AC＝3BF，其中正确的结论是.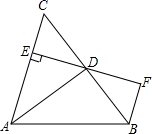
18. 如图，∠1+∠2+∠3+∠4+∠5＝°.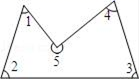
三、解答题
-
19. 如图所示，在△ABC中，D是BC边上一点，∠1=∠2，∠3=∠4，∠BAC=63°，求∠DAC的度数.
20.如图，已知AB∥CD，EF与AB、CD分别相交于点E、F，∠BEF与∠EFD的平分线相交于点P，求证：EP⊥FP．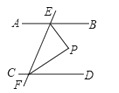
21. 如图，△ABC中，AD为∠BAC的平分线，且DF⊥AC于F，∠B=90°，DE=DC．求证：BE=CF．
