贵州省黔东南州三校联考2020-2021学年九年级上学期数学第一次月考试卷
试卷更新日期:2021-07-22 类型:月考试卷
一、单选题
-
1. 下列方程中,是二元一次方程的是( )A、2x-y=3 B、x+1=2 C、 D、x+y+z=12. 用配方法解一元二次方程 ,配方正确的是( ).A、 B、 C、 D、3. 已知 是一元二次方程 的一个根,则m的值为( )A、-1或2 B、-1 C、2 D、04. 已知二次函数 ,则下列关于这个函数图象和性质的说法,正确的是( )A、图象的开口向上 B、图象的顶点坐标是 C、当 时,y随x的增大而增大 D、图象与x轴有唯一交点5. 已知二次函数 ( 为常数)的图象与x轴有交点,且当 时,y随x的增大而增大,则a的取值范围是( )A、 B、 C、 D、6. 将二次函数y=(x﹣1)2+2的图象向上平移3个单位长度,得到的拋物线相应的函数表达式为( )A、y=(x+2)2﹣2 B、y=(x﹣4)2+2 C、y=(x﹣1)2﹣1 D、y=(x﹣1)2+57. 某年级举办篮球友谊赛,参赛的每两个队之间都要比赛一场,共要比赛36场,则参加此次比赛的球队数是( )A、6 B、7 C、8 D、98. 某校“研学”活动小组在一次野外实践时,发现一种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是 ,则这种植物每个支干长出的小分支个数是( )A、 B、 C、 D、9. 如图,直线 与抛物线 交于A、B两点,则 的图象可能是( )
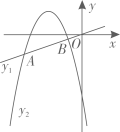 A、
A、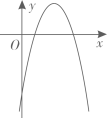 B、
B、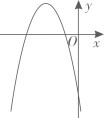 C、
C、 D、
D、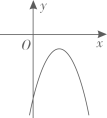 10. 抛物线y=ax2+bx+c的对称轴是直线x=﹣2.抛物线与x轴的一个交点在点(﹣4,0)和点(﹣3,0)之间,其部分图象如图所示,下列结论中正确的个数有( )
10. 抛物线y=ax2+bx+c的对称轴是直线x=﹣2.抛物线与x轴的一个交点在点(﹣4,0)和点(﹣3,0)之间,其部分图象如图所示,下列结论中正确的个数有( )①4a﹣b=0;②c≤3a;③关于x的方程ax2+bx+c=2有两个不相等实数根;④b2+2b>4ac.
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 一元二次方程 的解为 .12. 设 , 是方程 的两个实数根,则 的值为 .13. 请写出一个函数表达式,使其图象的对称轴为 轴:.14. 当﹣1≤x≤3时,二次函数y=x2﹣4x+5有最大值m,则m=.15. 抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,其与x轴的一个交点坐标为(﹣3,0),对称轴为x=﹣1,则当y<0时,x的取值范围是.
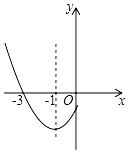 16. 方程 的两个根是等腰三角形的底和腰,则这个等腰三角形的周长为.17. 若正数a是一元二次方程x2﹣5x+m=0的一个根,﹣a是一元二次方程x2+5x﹣m=0的一个根,则a的值是 .
16. 方程 的两个根是等腰三角形的底和腰,则这个等腰三角形的周长为.17. 若正数a是一元二次方程x2﹣5x+m=0的一个根,﹣a是一元二次方程x2+5x﹣m=0的一个根,则a的值是 .
18. 设m、n是方程x2+x-1001=0的两个实数根,则m2+2m+n的值为.19. 如图,一名男生推铅球,铅球行进高度 (单位: )与水平距离 (单位: )之间的关系是 ,则他将铅球推出的距离是 .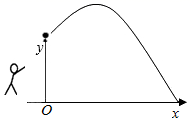 20. 体育公园的圆形喷水池的中央竖直安装了一个柱形喷水装置OA,A处为喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下 如图 如果曲线APB表示的是落点B离点O最远的一条水流 如图 ,水流喷出的高度 米 与水平距离 米 之间的关系式是 ,那么圆形水池的半径至少为米时,才能使喷出的水流不至于落在池外.
20. 体育公园的圆形喷水池的中央竖直安装了一个柱形喷水装置OA,A处为喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下 如图 如果曲线APB表示的是落点B离点O最远的一条水流 如图 ,水流喷出的高度 米 与水平距离 米 之间的关系式是 ,那么圆形水池的半径至少为米时,才能使喷出的水流不至于落在池外.
三、解答题
-
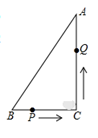
21. 关于x的一元二次方程 有两个实数根.(1)、求k的取值范围;(2)、请选择一个合适的数作为k的值,并求此时方程的根.22. 如图,在△ABC中,BC=7cm,AC=24cm,AB=25cm,P点在BC上,从B点到C点运动(不包括C点),点P运动的速度为2cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为5cm/s.若点P、Q分别从B、C同时运动,请解答下面的问题,并写出探索主要过程:
 (1)、经过多少时间后,P、Q两点的距离为5 cm?(2)、经过多少时间后, 的面积为15cm2?(3)、设运动时间为t,用含t的代数式表示△PCQ的面积,并用配方法说明t为何值时△PCQ的面积最大,最大面积是多少?23. 为了宣传垃圾分类,小王写了一封倡议书,用微博转发的方式传播,他设计了如下的转发规则:将倡议书发表在自己的微博上,然后邀请x个好友转发,每个好友转发之后,又邀请x个互不相同的好友转发,已知经过两轮转发后,共有111个人参与了本次活动。(1)、x的值是多少?(2)、再经过几轮转发后,参与人数会超过10000人?24. 某水产养殖户,一次性收购了 小龙虾,计划养殖一段时间后再出售.已知每天放养的费用相同,放养 天的总成本为 万元;放养 天的总成本为 万元(总成本=放养总费用+收购成本).(1)、设每天的放养费用是 万元,收购成本为 万元,求 和 的值;(2)、设这批小龙虾放养 天后的质量为 ( ),销售单价为 元/ .根据以往经验可知:m与t的函数关系式为 ,y与t的函数关系如图所示
(1)、经过多少时间后,P、Q两点的距离为5 cm?(2)、经过多少时间后, 的面积为15cm2?(3)、设运动时间为t,用含t的代数式表示△PCQ的面积,并用配方法说明t为何值时△PCQ的面积最大,最大面积是多少?23. 为了宣传垃圾分类,小王写了一封倡议书,用微博转发的方式传播,他设计了如下的转发规则:将倡议书发表在自己的微博上,然后邀请x个好友转发,每个好友转发之后,又邀请x个互不相同的好友转发,已知经过两轮转发后,共有111个人参与了本次活动。(1)、x的值是多少?(2)、再经过几轮转发后,参与人数会超过10000人?24. 某水产养殖户,一次性收购了 小龙虾,计划养殖一段时间后再出售.已知每天放养的费用相同,放养 天的总成本为 万元;放养 天的总成本为 万元(总成本=放养总费用+收购成本).(1)、设每天的放养费用是 万元,收购成本为 万元,求 和 的值;(2)、设这批小龙虾放养 天后的质量为 ( ),销售单价为 元/ .根据以往经验可知:m与t的函数关系式为 ,y与t的函数关系如图所示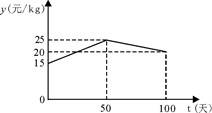
①求y与t的函数关系式;
②设将这批小龙虾放养t天后一次性出售所得利润为W元,求当 为何值时,W最大?并求出W的最大值.(利润=销售总额-总成本)
25. 把抛物线 先向右平移4个单位长度,再向下平移5个单位长度得到抛物线 .(1)、直接写出抛物线 的函数关系式;(2)、动点 能否在拋物线 上?请说明理由;(3)、若点 都在抛物线 上,且 ,比较 的大小,并说明理由.26. 已知抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在点B的左边),与y轴交于点C(0,﹣3),顶点D的坐标为(1,﹣4).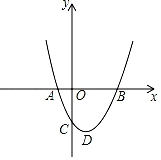 (1)、求抛物线的解析式.(2)、在y轴上找一点E,使得△EAC为等腰三角形,请直接写出点E的坐标.(3)、点P是x轴上的动点,点Q是抛物线上的动点,是否存在点P、Q,使得以点P、Q、B、D为顶点,BD为一边的四边形是平行四边形?若存在,请求出点P、Q坐标;若不存在,请说明理由.
(1)、求抛物线的解析式.(2)、在y轴上找一点E,使得△EAC为等腰三角形,请直接写出点E的坐标.(3)、点P是x轴上的动点,点Q是抛物线上的动点,是否存在点P、Q,使得以点P、Q、B、D为顶点,BD为一边的四边形是平行四边形?若存在,请求出点P、Q坐标;若不存在,请说明理由.