黑龙江省鹤岗市重点高中2020-2021学年高二下学期理数期末考试试卷
试卷更新日期:2021-07-22 类型:期末考试
一、选择题(本大题共有12个小题,每小题5分,共60分,在每小题给出的四选项中只有一项是符合题目要求的)
-
1. 已知 , ,则 ( )A、 B、 C、 D、2. 已知 是虚数单位,则复数 的虚部为( )A、 B、 C、 D、3. 下列函数中,是偶函数且值域为 的是( )A、 B、 C、 D、4. 函数 的大致图象是( )A、
 B、
B、 C、
C、 D、
D、 5. 已知幂函数 的图象过点 ,则 ( )A、2 B、3 C、8 D、96. 已知 是定义在 上的周期为4的奇函数,若当 时, ,则 ( )A、-1 B、0 C、1 D、27. 已知函数 的图象在 处的切线与直线 垂直。执行如图所示的程序框图,若输出的 的值为 ,则判断框中 的值可以为( )
5. 已知幂函数 的图象过点 ,则 ( )A、2 B、3 C、8 D、96. 已知 是定义在 上的周期为4的奇函数,若当 时, ,则 ( )A、-1 B、0 C、1 D、27. 已知函数 的图象在 处的切线与直线 垂直。执行如图所示的程序框图,若输出的 的值为 ,则判断框中 的值可以为( )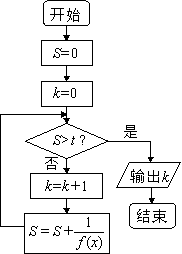 A、 B、 C、 D、8. 已知函数 为 上的偶函数,对任意 , ,均有
A、 B、 C、 D、8. 已知函数 为 上的偶函数,对任意 , ,均有成立,若 ,则 的大小关系是( )
A、 B、 C、 D、9. 曲线 在 处的切线与坐标轴围成的三角形面积为( )A、e B、 C、 D、10. 已知函数 ,则不等式 的解集为( )A、 B、 C、 D、11. 已知函数 ,若方程 恰有4个不同的实数根,则实数 的取值范围是( )A、 B、 C、 D、12. 已知定义在 上的函数 的导函数为 ,且满足 ,则关于 不等式 的解集为( )A、 B、 C、 D、二、填空题(本大题共有4个小题,每小题5分,共20分)
-
13. 若实数 , 满足 ,则 的最小值为.14.15. 设有下列四个命题:
: , ; : , ;
:方程 有两个不相等实根; :函数 的最小值是2.
则下述命题中所有真命题的序号是 .
① ;② ;③ ;④ .
16. 已知函数 , ,且 , , , 恒成立,则实数 的取值范围是 .三、解答题(本大题共有6个小题,共70分,第17题,10分,其余小题,每题12分。解答应写出文字说明、证明过程或演算步骤)
-
17. 化简并求值:(1)、(2)、 .18. 已知函数 .(1)、当 , 时,求函数 的值域;(2)、若函数 在 上的最大值为1,求实数 的值.19. 定义在 上的函数 是单调函数,满足 ,且 ,( , ).(1)、求 , ;(2)、判断 的奇偶性,并证明;(3)、若对于任意 ,都有 成立,求实数 的取值范围.