初中数学北师大版九年级上学期 第一章 1.3 正方形的性质与判定
试卷更新日期：2021-07-21 类型：同步测试
一、单选题
-
1. 下列不能判断是正方形的有（ ）A、对角线互相垂直的矩形 B、对角线相等的矩形 C、对角线互相垂直且相等的平行四边形 D、对角线相等的菱形2. 下列说法正确的个数是（ ）
①对角线互相垂直或有一组邻边相等的矩形是正方形；②对角线相等或有一个角是直角的菱形是正方形；③对角线互相垂直且相等的平行四边形是正方形；④对角线互相垂直平分且相等的四边形是正方形.
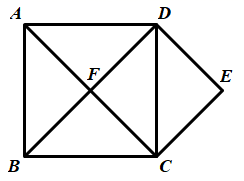
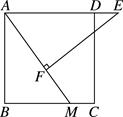
A、1个 B、2个 C、3个 D、4个3. 正方形ABCD中，对角线AC、BD交于点O，则∠CBO等于（ ）A、30° B、45° C、60° D、75°4. 如图，四边形ABCD是正方形，延长BC到E，使 ，连接AE交CD于点F，则 （ ）
A、67.5° B、65° C、55° D、45°5. 正方形的一条对角线之长为4,则此正方形的面积是（ ）A、16 B、4 C、8 D、86. 一个四边形顺次添加下列中的三个条件便得到正方形：
a.两组对边分别相等 b.一组对边平行且相等
c.一组邻边相等 d.一个角是直角
顺次添加的条件：①a→c→d②b→d→c③a→b→c
则正确的是（ ）
A、仅① B、仅③ C、①② D、②③7. 如图，四边形 是正方形， 是坐标原点，对角线 ， 分别位于 轴和 轴上，点 的坐标是 ，则正方形 的周长是（ ）
A、 B、12 C、 D、8. 如图是由七巧板拼成的正方形，则小正方形和大正方形的面积之比是（ ）
A、1：4 B、1：6 C、1：8 D、1：99. 如图，正方形ABCD的边长为1，点P为BC上任意一点（可与点B或C重合），分别过B、C、D作射线AP的垂线，垂足分别是B′、C′、D′，则BB′＋CC′＋DD′的最小值是（ ）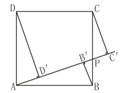
A、1 B、 C、 D、二、填空题
-
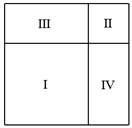
10. 若一个正方形的面积为a2+a+ ，则此正方形的周长为.11. 如图，两个正方形Ⅰ，Ⅱ和两个矩形Ⅲ，Ⅳ拼成一个大正方形，已知正方形Ⅰ，Ⅱ的面积分别为10和3，那么大正方形的面积是.
12. 如图，平行四边形ABCD的对角线互相垂直，要使ABCD成为正方形，还需添加的一个条件是（只需添加一个即可）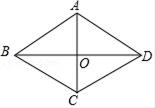
13. 若一个正方形的面积是12，则它的边长是 ．14. 如图，三个边长均为2的正方形重叠在一起，O1 ， O2是其中两个正方形的对角线交点，若把这样的n个小正方形按如图所示方式摆放，则重叠部分的面积为 ．
15. 如图，正方形ABCD中，AE＝2cm，CG＝5cm．长方形EFGD的面积是11，四边形NGDH和MEDQ都是正方形，PQDH是长方形，则图中阴影部分的面积是cm2 ．
16. 把图1中长和宽分别为3和2的两个全等矩形沿对角线分成四个全等的直角三角形，将这四个全等的直角三角形拼成图2所示的正方形，则图2中小正方形ABCD的面积为 ．
17. 如图，在△ABC中，分别以AB，AC为边向外作正方形ABED，ACGF。若点E，A，G在同一直线上，EG=8 ，BC=7，则△ABC的面积为。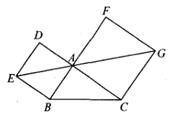
18. 如图，正方形ABCD的对角线长为8，E为AB上一点，若EF⊥AC于点F，EG⊥BD于点G，则EF+EG＝.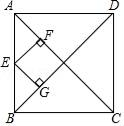
三、解答题
