内蒙古赤峰市2021年中考数学试卷
试卷更新日期:2021-07-20 类型:中考真卷
一、单选题
-
1. -2021的相反数是( )A、2021 B、-2021 C、 D、2. 截至北京时间2021年1月3日6时,我国执行首次火星探测任务的“天问一号”火星探测器已经在轨飞行约163天,飞行里程突破4亿公里,距离地球接近1.3亿公里,距离火星约830万公里,数据8300000用科学记数法表示为( )A、8.3×105 B、8.3×106 C、83×105 D、0.83×1073. 下列垃圾分类标识的图案既是轴对称图形,又是中心对称图形的是( )A、
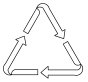 B、
B、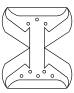 C、
C、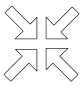 D、
D、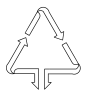 4. 下列说法正确的是( )A、“清明时节雨纷纷”是必然事件 B、为了了解一批灯管的使用寿命,可以采用普查的方式进行 C、一组数据2,5,4,5,6,7的众数、中位数和平均数都是5 D、甲、乙两组队员身高数据的方差分别为 , ,那么乙组队员的身高比较整齐5. 下列计算正确的是( )A、 B、 C、 D、6. 如图,AB∥CD,点E在线段BC上,CD=CE.若∠ABC=30°,则∠D为( )
4. 下列说法正确的是( )A、“清明时节雨纷纷”是必然事件 B、为了了解一批灯管的使用寿命,可以采用普查的方式进行 C、一组数据2,5,4,5,6,7的众数、中位数和平均数都是5 D、甲、乙两组队员身高数据的方差分别为 , ,那么乙组队员的身高比较整齐5. 下列计算正确的是( )A、 B、 C、 D、6. 如图,AB∥CD,点E在线段BC上,CD=CE.若∠ABC=30°,则∠D为( ) A、85° B、75° C、60° D、30°7. 实数a、b、c在数轴上对应点的位置如图所示.如果 ,那么下列结论正确的是( )
A、85° B、75° C、60° D、30°7. 实数a、b、c在数轴上对应点的位置如图所示.如果 ,那么下列结论正确的是( )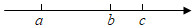 A、 B、 C、 D、8. 五一期间,某地相关部门对观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整),下列结论错误的是( )
A、 B、 C、 D、8. 五一期间,某地相关部门对观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整),下列结论错误的是( )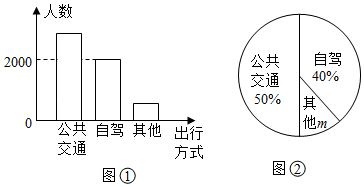 A、本次抽样调查的样本容量是5000 B、扇形统计图中的m为10% C、若五一期间观光的游客有50万人,则选择自驾方式出行的大约有20万人 D、样本中选择公共交通出行的有2400人9. 一元二次方程 ,配方后可形为( )A、 B、 C、 D、10. 如图,点C , D在以AB为直径的半圆上, ,点E是 上任意一点,连接BE , CE , 则 的度数为( )
A、本次抽样调查的样本容量是5000 B、扇形统计图中的m为10% C、若五一期间观光的游客有50万人,则选择自驾方式出行的大约有20万人 D、样本中选择公共交通出行的有2400人9. 一元二次方程 ,配方后可形为( )A、 B、 C、 D、10. 如图,点C , D在以AB为直径的半圆上, ,点E是 上任意一点,连接BE , CE , 则 的度数为( )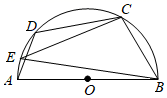 A、20° B、30° C、40° D、60°11. 点 在函数 的图象上,则代数式 的值等于( )A、5 B、-5 C、7 D、-612. 已知抛物线 上的部分点的横坐标x与纵坐标y的对应值如表:
A、20° B、30° C、40° D、60°11. 点 在函数 的图象上,则代数式 的值等于( )A、5 B、-5 C、7 D、-612. 已知抛物线 上的部分点的横坐标x与纵坐标y的对应值如表:x
…
-1
0
1
2
3
…
y
…
3
0
-1
m
3
…
以下结论正确的是( )
A、抛物线 的开口向下 B、当 时,y随x增大而增大 C、方程 的根为0和2 D、当 时,x的取值范围是13. 一个几何体的三视图如图所示,则这个几何体的侧面积是( )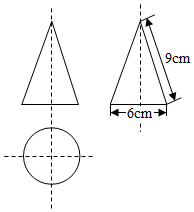 A、 B、 C、 D、14. 甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中甲、乙两人之间的距离 (米)与乙出发的时间x(秒)之间的函数关系如图所示,正确的个数为( )
A、 B、 C、 D、14. 甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中甲、乙两人之间的距离 (米)与乙出发的时间x(秒)之间的函数关系如图所示,正确的个数为( )①乙的速度为5米/秒;②离开起点后,甲、乙两人第一次相遇时,距离起点12米;③甲、乙两人之间的距离超过32米的时间范围是 ;④乙到达终点时,甲距离终点还有68米.
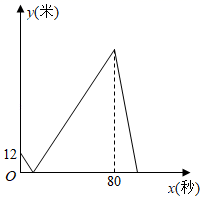 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
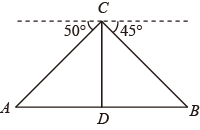
15. 在函数 中,自变量x的取值范围是.16. 某滑雪场用无人机测量雪道长度.如图,通过无人机的镜头C测一段水平雪道一端A处的俯角为50°,另一端B处的俯角为45°,若无人机镜头 处的高度 为 米,点A , D , B在同一直线上,则通道AB的长度为米.(结果保留整数,参考数据 , , )
 17. 如图,在拧开一个边长为a的正六角形螺帽时,扳手张开的开口b=20mm,则边长a为mm.
17. 如图,在拧开一个边长为a的正六角形螺帽时,扳手张开的开口b=20mm,则边长a为mm.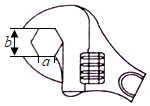 18. 如图,正方形ABCD的边长为 ,点E是BC的中点,连接CG并延长,交AB于点F , 连接AH . 以下结论:①CF⊥DE;② ;③ ,④ ,其中正确结论的序号是 .
18. 如图,正方形ABCD的边长为 ,点E是BC的中点,连接CG并延长,交AB于点F , 连接AH . 以下结论:①CF⊥DE;② ;③ ,④ ,其中正确结论的序号是 .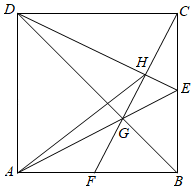
三、解答题
-
19. 先化简,再求值: ,其中 .20. 如图,在Rt△ABC中,∠ACB=90°,且AC=AD .
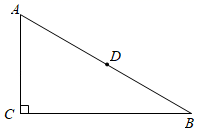 (1)、作∠BAC的平分线,交BC于点E;(要求尺规作图,不写作法,保留作图痕迹)(2)、在(1)的条件下,连接DE , 证明 .21. 某学校九年级有12个班,每班50名学生,为了调查该校九年级学生平均每天的睡眠时间,并规定如下:设每个学生平均每天的睡眠时间为t(单位,小时),将收集到的学生平均每天睡眠时间按t≤6、6<t<8、t≥8分为三类进行分析.(1)、下列抽取方法具有代表性的是( )。A、随机抽取一个班的学生 B、从12个班中,随机抽取50名学生 C、随机抽取50名男生 D、随机抽取50名女生(2)、由上述具有代表性的抽取方法抽取50名学生,平均每天的睡眠时间数据如表:
(1)、作∠BAC的平分线,交BC于点E;(要求尺规作图,不写作法,保留作图痕迹)(2)、在(1)的条件下,连接DE , 证明 .21. 某学校九年级有12个班,每班50名学生,为了调查该校九年级学生平均每天的睡眠时间,并规定如下:设每个学生平均每天的睡眠时间为t(单位,小时),将收集到的学生平均每天睡眠时间按t≤6、6<t<8、t≥8分为三类进行分析.(1)、下列抽取方法具有代表性的是( )。A、随机抽取一个班的学生 B、从12个班中,随机抽取50名学生 C、随机抽取50名男生 D、随机抽取50名女生(2)、由上述具有代表性的抽取方法抽取50名学生,平均每天的睡眠时间数据如表:睡眠时间t(小时)
5
5.5
6
6.5
7
7.5
8
8.5
人数(人)
1
1
2
10
15
9
10
2
①这组数据的众数和中位数分别是 ▲ , ▲ ;
②估计九年级学生平均每天睡眼时间 的人数大约为多少;
(3)、从样本中学生平均每天睡眠时间 的4个学生里,随机抽取2人,画树状图或列表法求抽取的2人每天睡眠时间都是6小时的概率.22. 为传承优秀传统文化,某地青少年活动中心计划分批次购进四大名著:《西游记》、《水浒传》、《三国演义》、《红楼梦》.第一次购进《西游记》50本,《水浒传》60本,共花费6600元,第二次购进《西游记》40本,《水浒传》30本,共花费4200元.(1)、求《西游记》和《水浒传》每本的售价分别是多少元;(2)、青少年活动中心决定再购买上述四种图书,总费用不超过32000元.如果《西游记》比《三国演义》每本售价多10元,《水浒传》比《红楼梦》每本售价少10元(四大名著各一本为一套),那么这次最多购买《西游记》多少本?23. 阅读理解:在平面直角坐标系中,点M的坐标为 ,点N的坐标为 ,且x1≠x1 , y2≠y2 , 若M、N为某矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为M、N的“相关矩形”.如图1中的矩形为点M、N的“相关矩形”.
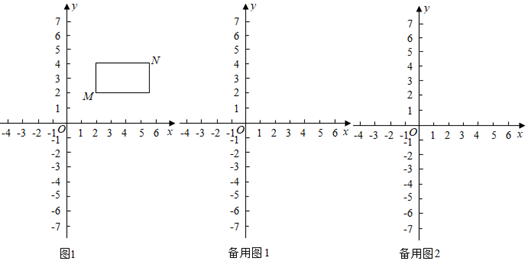 (1)、已知点A的坐标为 .
(1)、已知点A的坐标为 .①若点B的坐标为 ,则点A、B的“相关矩形”的周长为 ▲ ;
②若点C在直线x=4上,且点A、C的“相关矩形”为正方形,求直线AC的解析式;
(2)、已知点P的坐标为 ,点Q的坐标为 , 若使函数 的图象与点P、Q的“相关矩形 ”有两个公共点,直接写出k的取值范围.24. 如图,在菱形ABCD中,对角线AC、BD相交于点M , C , 交对角线BD于点E , 且 ,连接OE交BC于点F .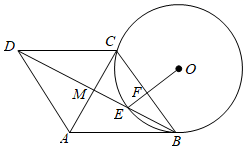 (1)、试判断AB与⊙O的位置关系,并说明理由;(2)、若 , ,求⊙O的半径.25. 如图,抛物线 与x轴交于 、 两点,对称轴l与x轴交于点F , 直线m AC , 过点E作EH⊥m , 垂足为H , 连接AE、EC、CH、AH .
(1)、试判断AB与⊙O的位置关系,并说明理由;(2)、若 , ,求⊙O的半径.25. 如图,抛物线 与x轴交于 、 两点,对称轴l与x轴交于点F , 直线m AC , 过点E作EH⊥m , 垂足为H , 连接AE、EC、CH、AH .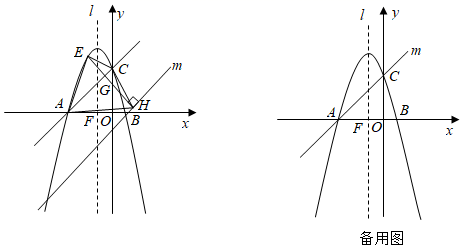 (1)、抛物线的解析式为;(2)、当四边形AHCE面积最大时,求点E的坐标;(3)、在(2)的条件下,连接EF , 点P在x轴上,在抛物线上是否存在点Q , 使得以F、E、P、Q为顶点的四边形是平行四边形,请直接写出点Q的坐标;若不存在请说明理由.26. 数学课上,有这样一道探究题.
(1)、抛物线的解析式为;(2)、当四边形AHCE面积最大时,求点E的坐标;(3)、在(2)的条件下,连接EF , 点P在x轴上,在抛物线上是否存在点Q , 使得以F、E、P、Q为顶点的四边形是平行四边形,请直接写出点Q的坐标;若不存在请说明理由.26. 数学课上,有这样一道探究题.
如图,已知△ABC中,AB=AC=m,BC=n,∠BAC=α(0°<α<180°),点P为平面内不与点A、C重合的任意一点,连接CP,将线段CP绕点P顺时针旋转α,得线段PD,连接CD、AP点E、F分别为BC、CD的中点,设直线AP与直线EF相交所成的较小角为β,探究的的值 和β的度数与m、n、α的关系.
请你参与学习小组的探究过程,并完成以下任务: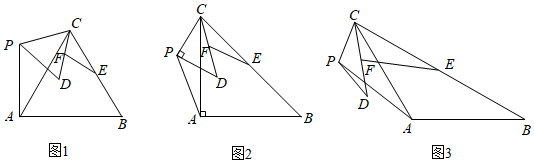
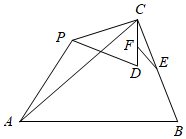 (1)、【问题发现】 填空:
(1)、【问题发现】 填空:小明研究了α=60°时,如图1,求出了的值 和β的度数分别为 , ;
小红研究了α=90°时,如图2,求出了的值 和β的度数分别为 , ;
【类比探究】
他们又共同研究了α=120°时,如图3,也求出了 的值和β的度数;
【归纳总结】
最后他们终于共同探究得出规律:(用含m、n的式子表示); (用含α的式子表示).
(2)、求出 时 的值和 的度数.